PyTorch中的nn.Conv1d、nn.Conv2d以及文本卷积
- 简单理解文本处理时的卷积原理
- 一维卷积nn.Conv1d
- 定义
- 参数说明
- 代码示例
- 涉及论文及图解
- 二维卷积nn.Conv2d
- 定义
- 参数说明
- 代码示例
- 图解
- 总结
大多数 NLP 任务的输入不是图像像素,而是以矩阵表示的句子或文档。矩阵的每一行对应一个标记,通常是一个单词,但它也可以是一个字符。也就是说,每一行都是代表一个单词的向量。通常这些向量是像 word2vec 或 GloVe 这样的词嵌入(低维表示),但是它们也可以是将单词索引到词汇表中的一个 one-hot 向量。对于使用 100 维嵌入的 10 个字的句子,我们将有一个 10×100 的矩阵作为我们的输入。这就是是我们的“图像”。
在计算机视觉上,我们的过滤器在图像的局部区域上滑动,但是在 NLP 中,我们通常使用滑过整行矩阵(单词)的过滤器。因此,我们的滤波器的“宽度”通常与输入矩阵的宽度相同。对于矩阵的宽度其实就是一个单词转化为的词向量的长度,然后这个滤波器相当于一次遍历多个词向量,而且可以有不同的滤波器。高度或区域大小可能会有所不同,通常使用一次滑动 2-5 个字的窗口。
一维卷积nn.Conv1d一般用于文本数据,只对宽度进行卷积,对高度不卷积。通常,输入大小为word_embedding_dim * max_length,其中,word_embedding_dim为词向量的维度,max_length为句子的最大长度。卷积核窗口在句子长度的方向上滑动,进行卷积操作。
class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- :在文本应用中,即为词向量的维度
- :卷积产生的通道数,有多少个,就需要多少个一维卷积(也就是卷积核的数量)
- :卷积核的尺寸;卷积核的第二个维度由决定,所以实际上卷积核的大小为
- :对输入的每一条边,补充0的层数
Yoon Kim在2014年发表的论文Convolutional Neural Networks for Sentence Classification中给出如下的图,一个用于 NLP 的卷积神经网络可能看起来像这样。
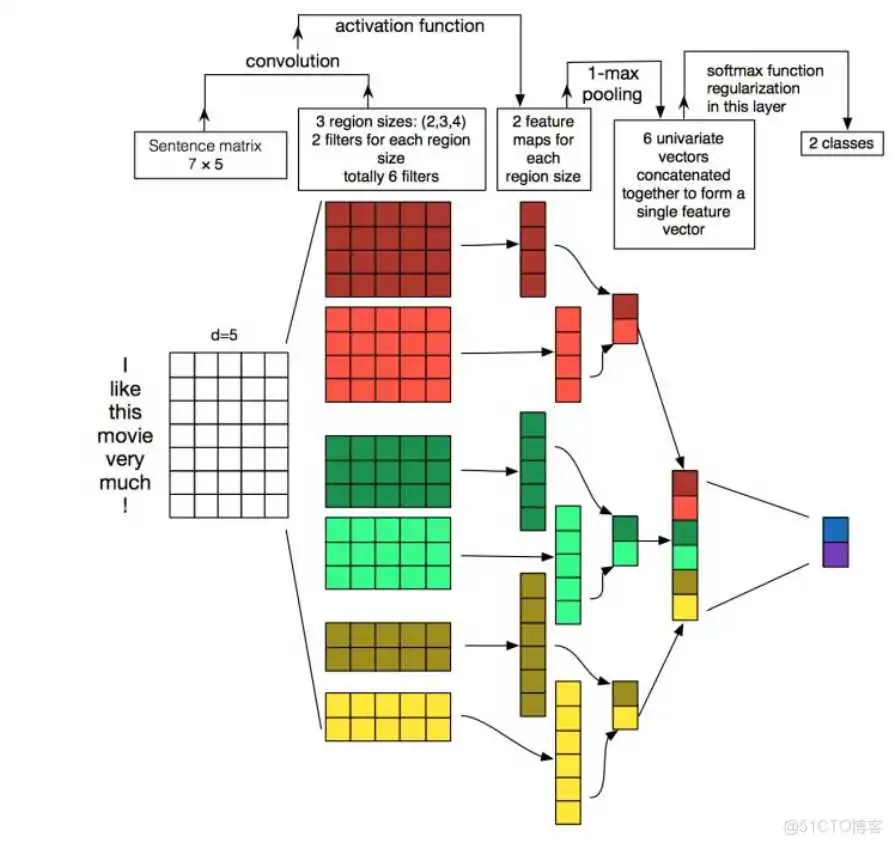
用于句子分类的卷积神经网络(CNN)体系结构图。 这里描述了三个过滤器的大小:,每个大小都有个过滤器。 每个过滤器对句子矩阵执行卷积并生成(可变长度)特征映射。 然后在每个特征图上执行池化,即记录来自每个特征图的最大数。 因此,从六个特征图生成一元特征向量,并且这六个特征被连接以形成倒数第二层的特征向量。 最后的接收这个特征向量作为输入,并用它来分类句子;这里我们假设二进制分类,因此描述了两种可能的输出状态。
CNN的一个重要论点是,它们很快。非常快。卷积是计算机图形的核心部分,并在 GPUs 上的硬件级别上实现。与 n-grams 相比,CNNs 在表达方面也是有效的。有了大量的词汇,计算超过 3-grams 的任何东西都可能很快变得昂贵。即使是 Google 也不提供超过 5-grams 的任何东西。卷积过滤器自动学习好的表征,而不需要表示整个词汇表。我认为,第一层中的许多学习过滤器捕获与 n-gram 非常相似(但不限于)的特征,但是以更紧凑的方式表示它们。
一般来说,二维卷积用于图像数据,对宽度和高度都进行卷积。
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- :在文本应用中,即为词向量的维度
- :卷积产生的通道数,有多少个,就需要多少个一维卷积(也就是卷积核的数量)
- :卷积核的尺寸;卷积核的第二个维度由决定,所以实际上卷积核的大小为
- :对输入的每一条边,补充0的层数
假设现有大小为的图片样本,输入样本的channels为1,该图片可能属于10个类中的某一类。CNN框架定义如下:
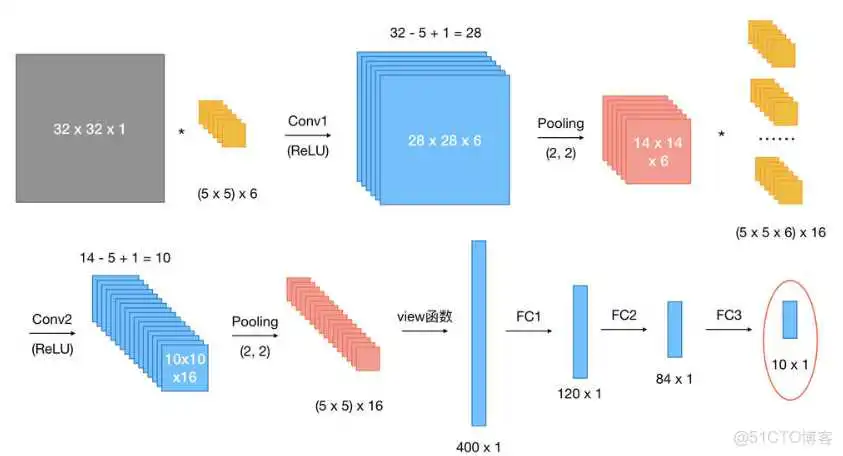
网络整体结构: 原始输入样本的大小:
- 第一次卷积:使用个大小为的卷积核,故卷积核的规模为;卷积操作的stride参数默认值为,32 - 5 + 1 = 28,并且使用ReLU对第一次卷积后的结果进行非线性处理,输出大小为;
- 第一次卷积后池化:kernel_size为,输出大小变为;
- 第二次卷积:使用个卷积核,故卷积核的规模为;使用ReLU对第二次卷积后的结果进行非线性处理,14 - 5 + 1 = 10,故输出大小为;
- 第二次卷积后池化:kernel_size同样为,输出大小变为;
- 第一次全连接:将上一步得到的结果铺平成一维向量形式,5 x 5 x 16 = 400,即输入大小为,W大小为,输出大小为;
- 第二次全连接:W大小为84 x 120,输入大小为,输出大小为;
- 第三次全连接:W大小为,输入大小为``84 x 1,输出大小为,即分别预测为10类的概率值。
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/rfx/40427.html
