作者:CSDN @ _养乐多_
背景
一维卷积的运算过程网上很多人说不清楚,示意图画的也不清楚。因此,本人针对一维卷积的过程,绘制了计算过程,以我的知识量解释一下 pytorch 中 Conv1d() 函数的机理。
Conv1d() 计算过程
假设我们现在有 n 行,3列数据。n 行可以是 n 个点,也可以是 n 个样本数据。3列可以视为3列特征,即特征向量。我们想要通过 MLP 将其从3列升维度为6维度,就需要用 Conv1d() 函数。具体过程就是让每一行数据点乘一个卷积核,得到一个数,6个卷积核就是6个数,这样就把一个点的3列变成了6列。然后逐行遍历每个点,就可以得到新的得分矩阵。
备注: 从6列变成12列,就点乘12个卷积核。从12列变成6列,就点乘6个卷积核。
Conv1d() 计算过程图示
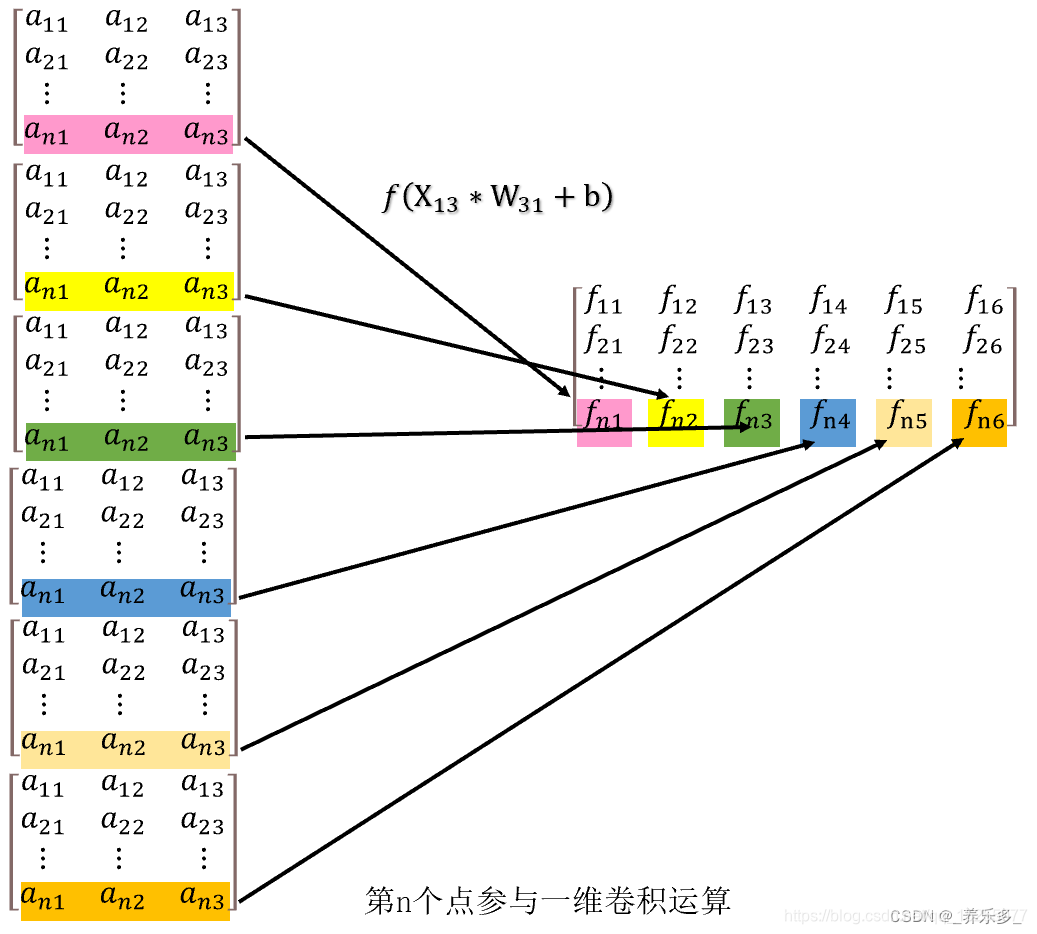
①、第1行数据参与卷积(这里的 a 是样本数据,W 是卷积核,f 是结果。)

②、第2行数据参与卷积

③、第n行数据参与卷积
Conv1d() 代码举例
我们以 PointNet 中分类的主干模型 (多层感知机,MLP) 来说,Conv1d(64, 128, 1) 其实就是用 128 个 64 行 1 列的卷积核和前面 n 行 64 列的矩阵逐行点积,升维到 128 列。
Linear() 的原理
就是解 Y = X · A.T + b。其中的 A.T 是权重矩阵的转置矩阵,b 为偏置矩阵。nn.Linear(1024, 512) 就是将 n 行 1024 列的 X 矩阵降维到 n 行 512 列的矩阵。只要 A.T 为 1024 行 512 列的矩阵,和 X 点乘,就可以得到 n 行 512 列的矩阵,达到降维的目的。
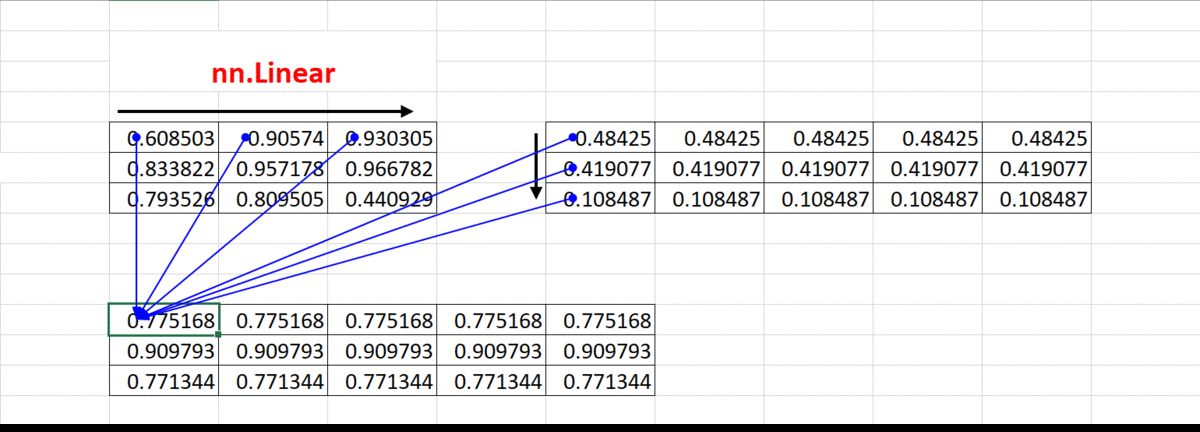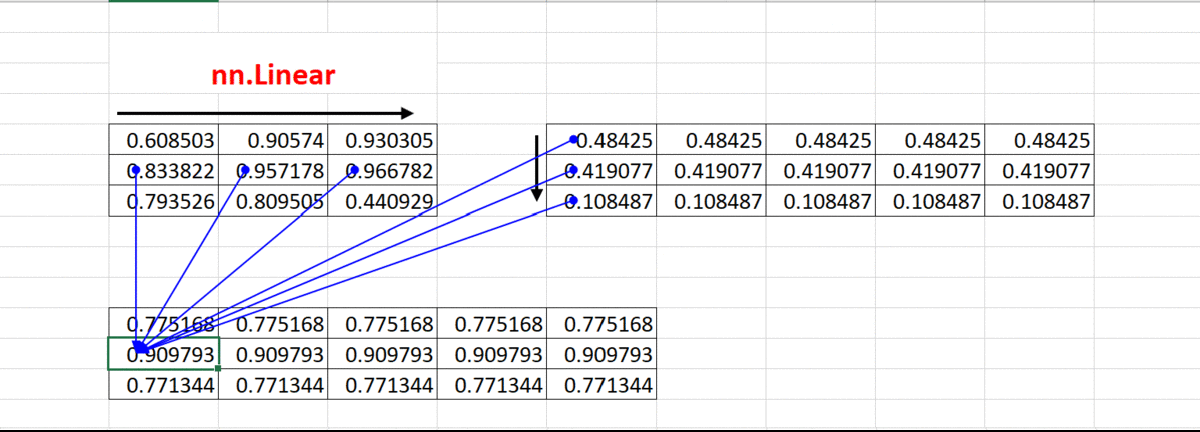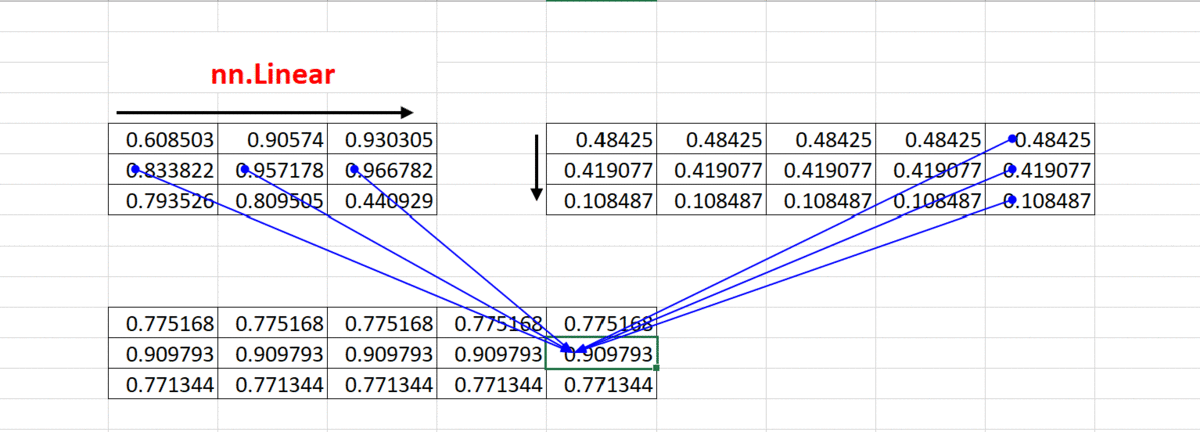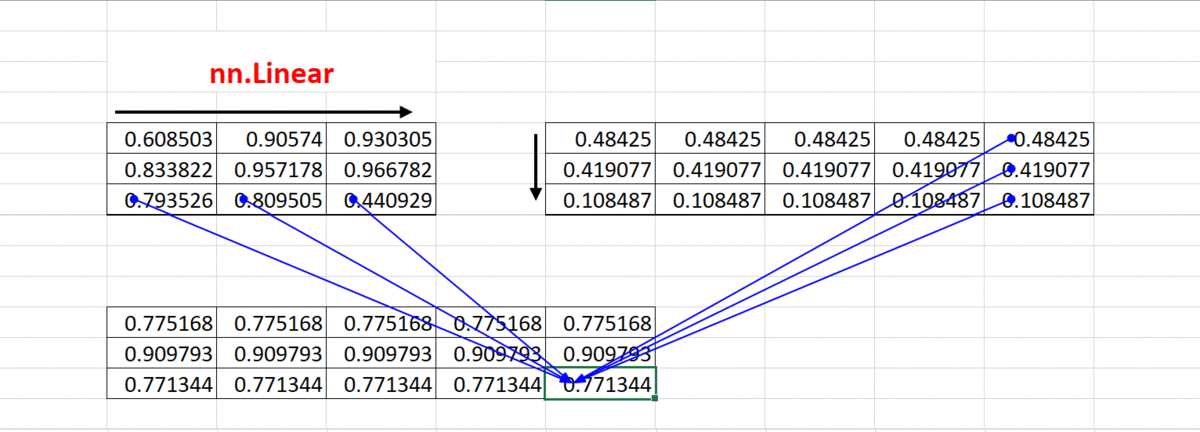
①、Linear() 计算 (忽略偏置矩阵)

Linear() 动图
Conv1d() 和 Linear() 的区别
已经有人比较了在相同输入数据的条件下两者之间的区别:(1)Linear() 比 conv1d() 的计算速度快;(2)Conv1d() 的精度比 Linear() 的高;(3)在反向传播更新梯度的时候,数值有差异。
那么为什么这么设计呢?查了大量资料以后,我觉得这个答案最靠谱。当你必须保留语义分割中的空间信息时,使用卷积 Conv1d() 。当你不需要做任何与空间信息相关的事情时,比如在基本分类(mnist、猫狗分类器)中,使用线性层 Linear() 。
卷积核
到此这篇conv1d原理(conv1d linear)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/rfx/36369.html
