梯度提升树算法流程图（梯度提升树分类算法）

Machine learning is changing the world!

图源：于网络

0 1

随机梯度提升算法

上一章节中我们分享了基础GBM的相关知识，本节我们将进一步学习随机梯度提升算法（ Stochastic GBMs ）。

Breiman在开发装袋决策树和随机森林算法时提出，在训练集的随机子样本上训练算法可以进一步减少树的相关性，从而可以改进模型的表现性能。基于这一点，Friedman 使用相同的逻辑并相应地更新了梯度提升算法，这个过程被称为随机梯度提升算法。如下图所示，随机梯度提升算法有助于减少陷入局部最小值、最大值和其他不规则损失函数的机会，从而方便我们找到损失函数的最优值。

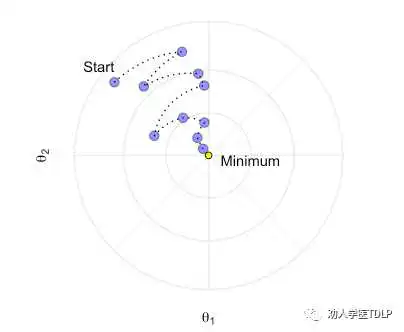
随机梯度下降通常会通过跳出局部最小值来找到接近最优的解决方案

0 2

随机超参数

目前有一些随机梯度提升算法的的衍生算法，每种衍生算法都有对应的额外的超参数：

在创建每棵树之前对行进行二次抽样（在 gbm、h2o 和 xgboost 中可用）
在创建每棵树之前对列进行二次抽样（h2o 和 xgboost）
在考虑每棵树中的每个拆分之前对列进行二次抽样（h2o 和 xgboost）

通常，对行进行二次抽样，例如仅选择 50% 或更少的观测对象，已证明对于提高模型的预测性能是有益的，典型值范围在 0.5-0.8 之间。对列进行二次抽样及其对性能的影响在很大程度上取决于数据本身的性质以及是否存在较强的多重共线性或大量噪声特征。与随机森林中的 mtry 参数类似，如果特征中相关的变量较少时（噪声数据较多），则较高的列重抽样往往会有更好的表现性能，因为这种情况下更有可能选择信号最强的那些特征。相反，当相关预测变量很多时，较低的列重抽样值所对应的模型表现性能会更好。

在基础GDM的基础上使用随机GBM时，我们可以在基础GBM一般调参策略中的步骤 4) 中添加随机GBM，或者在我们找到最佳基础GBM时（步骤六）。（基础GBM调参策略如下）

基础GBM调参策略

择相对较高的学习率。通常默认值 0.1 有效，但 0.05-0.2 之间的某个值应该适用于大多数问题。
确定此学习率的最佳树数目。
修复树超参数并调整学习率并评估速度与性能。
调优树特异参数以决定学习率。
找到树特异参数后，降低学习率以评估准确性是否有所提高。
使用最终的超参数设置并增加 CV 程序以获得更稳健的估计。通常，由于计算上限，上述步骤使用简单的验证程序或 5 折 CV 。如果在整个步骤 1-5 中使用了 k 折 CV，则不需要此步骤。

0 3

随机GBM算法的实现

目前有一些随机梯度提升算法的的衍生算法，每种衍生算法都有对应的额外的超参数

下面使用 h2o 来实现随机 GBM。我们使用在上一节中找到的最佳超参数，并通过在构建每棵树之前对行和列进行重抽样以及在每次拆分之前对列进行重抽样的不同值范围来评价我们构建的模型。

# Helper packageslibrary(tidyverse) # for general data wrangling needs
# Modeling packageslibrary(gbm) # for original implementation of regular and stochastic GBMslibrary(h2o) # for a java-based implementation of GBM variantslibrary(xgboost) # for fitting extreme gradient boosting
library(AmesHousing) #for loading ames datalibrary(rsample)# for data splitames<-make_ames() #loading ames data# Stratified sampling with the rsample packageset.seed(123)split <- initial_split(ames, prop = 0.7,  strata = "Sale_Price")ames_train <- training(split)ames_test <- testing(split)h2o.init(max_mem_size = "10g")
train_h2o <- as.h2o(ames_train)response <- "Sale_Price"predictors <- setdiff(colnames(ames_train), response)

运行随机GBM算法（以下会运行很长时间）！

# refined hyperparameter gridhyper_grid <- list( sample_rate = c(0.5, 0.75, 1), # row subsampling col_sample_rate = c(0.5, 0.75, 1), # col subsampling for each split col_sample_rate_per_tree = c(0.5, 0.75, 1) # col subsampling for each tree)
# random grid search strategysearch_criteria <- list( strategy = "RandomDiscrete", stopping_metric = "mse", stopping_tolerance = 0.001,  stopping_rounds = 10,  max_runtime_secs = 60*60 )
# perform grid search grid <- h2o.grid( algorithm = "gbm", grid_id = "gbm_grid", x = predictors,  y = response, training_frame = train_h2o, hyper_params = hyper_grid, ntrees = 6000, learn_rate = 0.01, max_depth = 7, min_rows = 5, nfolds = 10, stopping_rounds = 10, stopping_tolerance = 0, search_criteria = search_criteria, seed = 123)
# collect the results and sort by our model performance metric of choicegrid_perf <- h2o.getGrid( grid_id = "gbm_grid",  sort_by = "mse",  decreasing = FALSE)
grid_perf H2O Grid Details ================  Grid ID: gbm_grid  Used hyper parameters:  - col_sample_rate  - col_sample_rate_per_tree  - sample_rate  Number of models: 18  Number of failed models: 0   Hyper-Parameter Search Summary: ordered by increasing mse col_sample_rate col_sample_rate_per_tree sample_rate model_ids mse 1 0.5 0.5 0.5 gbm_grid_model_8 4.5138E8 2 0.5 1.0 0.5 gbm_grid_model_3 4.6835E8 3 0.5 0.75 0.75 gbm_grid_model_12 4.85947E8 4 0.75 0.5 0.75 gbm_grid_model_5 4.1389E8 5 1.0 0.75 0.5 gbm_grid_model_14 4.37276E8 6 0.5 0.5 0.75 gbm_grid_model_10 4.9245E8 7 0.75 1.0 0.5 gbm_grid_model_4 4.0368E8 8 1.0 1.0 0.5 gbm_grid_model_1 4.8762E8 9 1.0 0.75 0.75 gbm_grid_model_6 4.47874E8 10 0.75 1.0 0.75 gbm_grid_model_13 4.9563E8 11 0.75 0.5 1.0 gbm_grid_model_2 5.02187E8 12 0.75 0.75 0.75 gbm_grid_model_15 5.03763E8 13 0.75 0.75 1.0 gbm_grid_model_9 5.80266E8 14 0.75 1.0 1.0 gbm_grid_model_11 5.319E8 15 1.0 1.0 1.0 gbm_grid_model_7 6.0542E8 16 1.0 0.75 1.0 gbm_grid_model_16 1.19803E9 17 0.5 1.0 0.75 gbm_grid_model_17 4.39005E9 18 1.0 0.5 1.0 gbm_grid_model_18 5.8916E9

从网格搜索的结果可以看出，从每棵树的行中随机抽样和在每次拆分之前对特征进行随机抽样似乎都对模型的性能产生一定影响。在每棵树之前对特征进行随机抽样是否对模型性能有影响并不确定。此外，最佳重抽样值非常低（0.5）；进一步的网格搜索可能有助于评估更低的抽样值对结果的影响。

下面我们提取性能最好的模型。然而，在这种情况下，我们并没有看到10折 CV对应的 RMSE比非随机 GBM 模型有额外的改进。

# Grab the model_id for the top model, chosen by cross validation errorbest_model_id <- grid_perf@model_ids[[1]]best_model <- h2o.getModel(best_model_id)
# Now let’s get performance metrics on the best modelh2o.performance(model = best_model, xval = TRUE)## H2ORegressionMetrics: gbm## Reported on cross-validation data. ## 10-fold cross-validation on training data (Metrics computed for combined holdout predictions) ## ## MSE: ## RMSE: 21125.73## MAE: 13045.95## RMSLE: 0.## Mean Residual Deviance :

本节完，下节我们将学习XGBoost算法。

图源于网络

参考来源： Bradley Boehmke & Brandon Greenwell R与机器学习

往期推荐

R与机器学习系列|1.机器学习概论

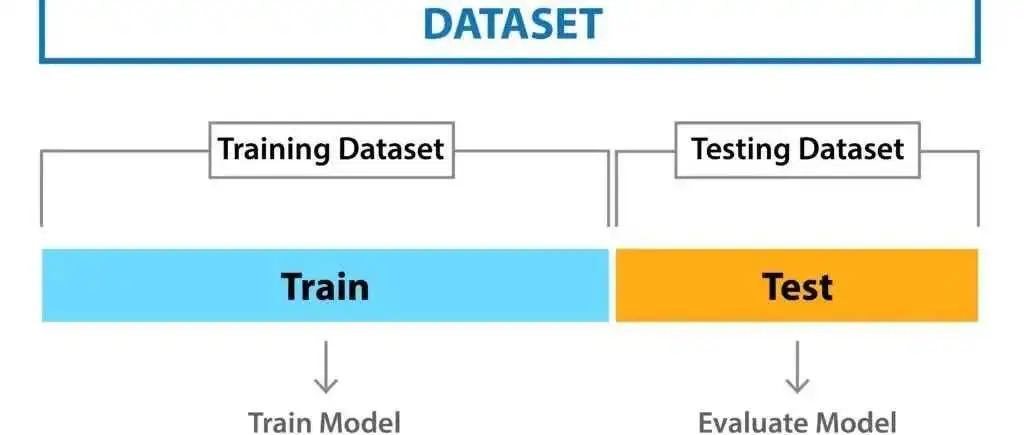
R与机器学习系列|2.机器学习模型建立过程（上）

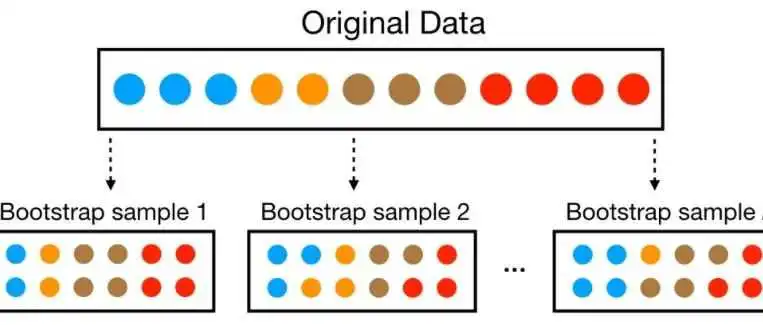
R与机器学习系列|2.机器学习模型建立过程（下）——重抽样方法

R与机器学习系列|2.机器学习模型建立过程（下）——偏差方差的权衡及超参数寻优

R与机器学习系列|2.机器学习模型建立过程（下）——模型评价指标及整体过程实现

R与机器学习系列|3.特征与目标工程（上）——目标工程及缺失值处理

R与机器学习系列|3.特征与目标工程（上）——缺失值处理及特征筛选

R与机器学习系列|3.特征与目标工程（下）——数值型数据特征工程

R与机器学习系列|3.特征与目标工程（下）——分类变量特征工程

R与机器学习系列|3.特征与目标工程（下）——降维及整体过程实现

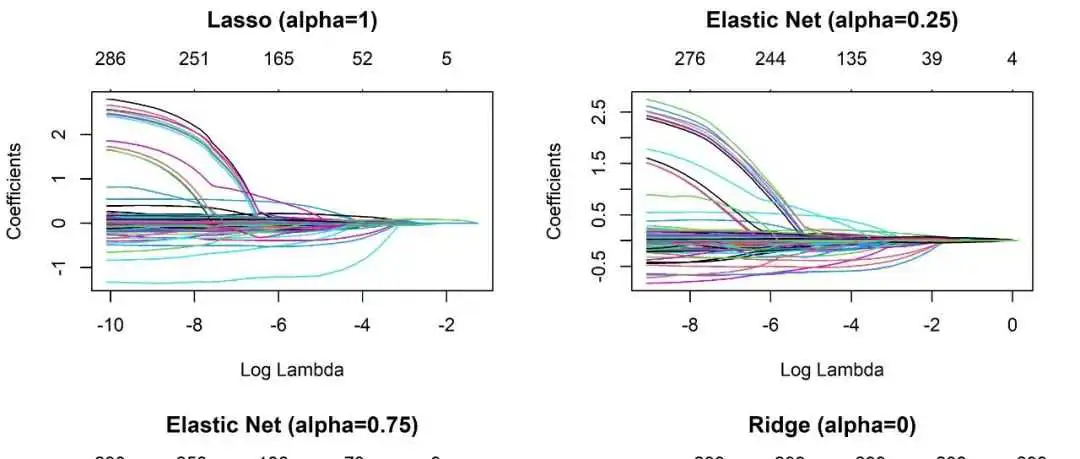
R与机器学习系列|4.正则化回归（Regularized Regression）

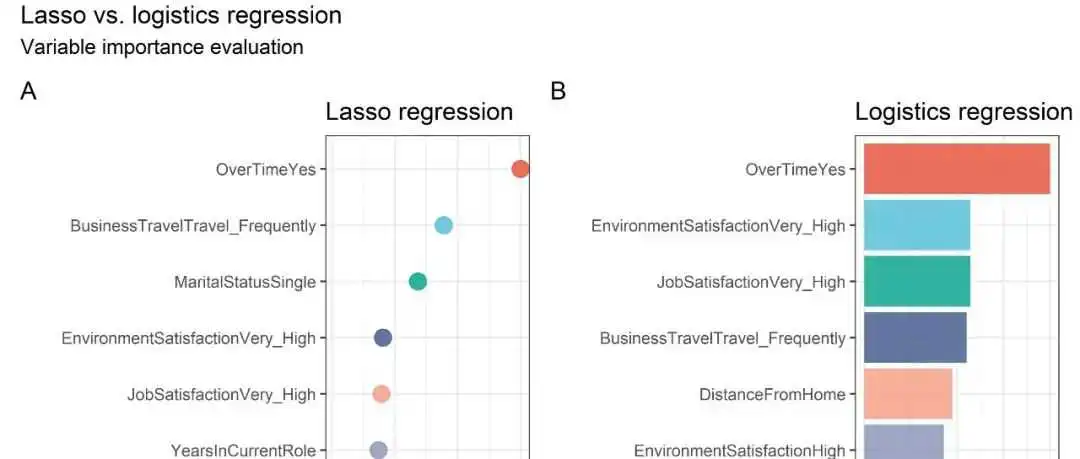
R与机器学习系列|4.正则化回归（Regularized Regression）（下）

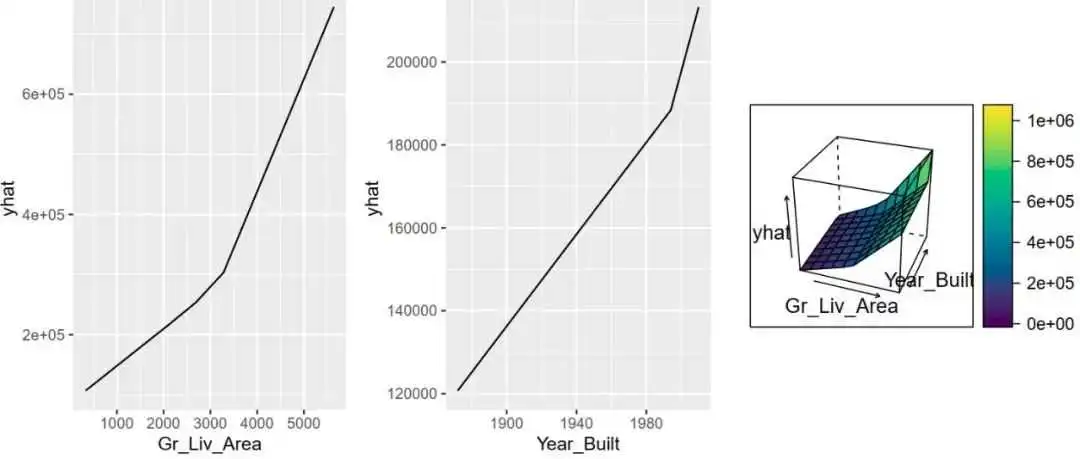
R与机器学习系列|5.多元自适应回归样条（Multivariate Adaptive Regression Splines）

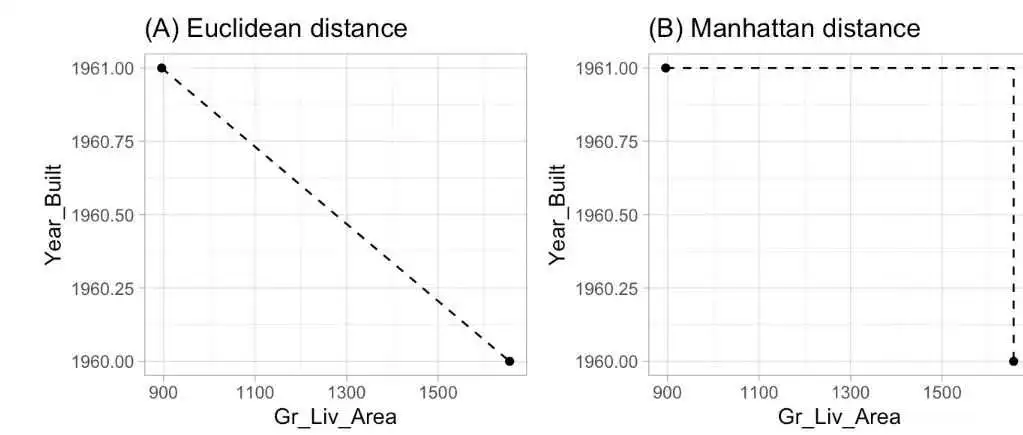
R与机器学习系列|6.k-近邻算法(k-NearestNeighbor，KNN）

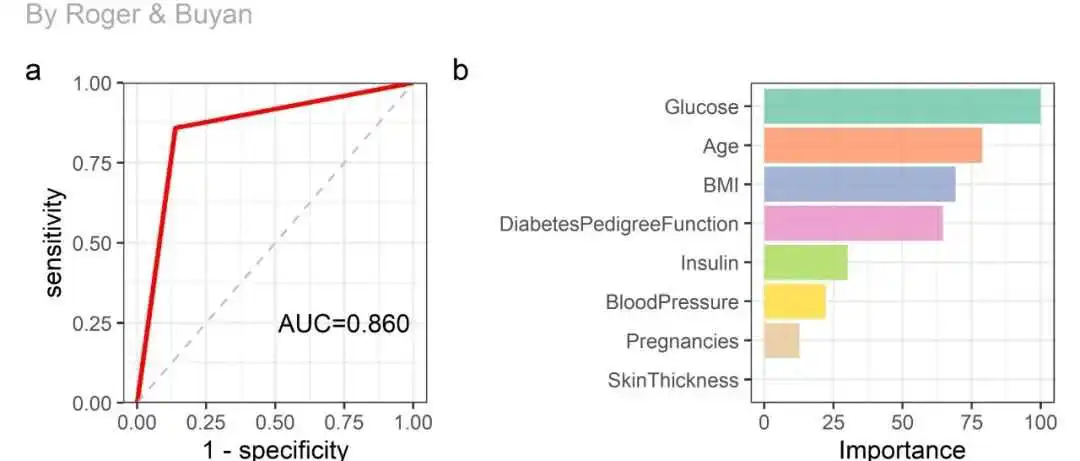
R与机器学习系列|7.决策树(Decision Trees)

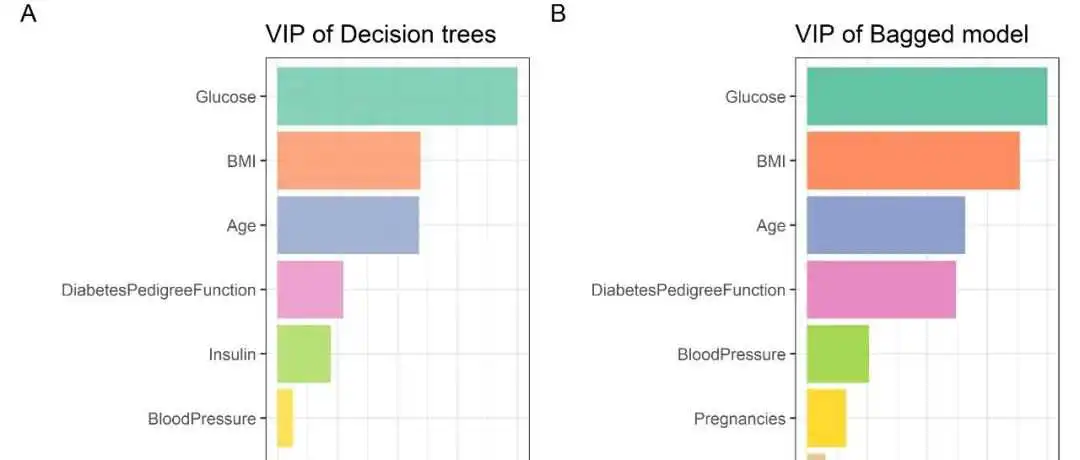
R与机器学习系列|8.Bagging

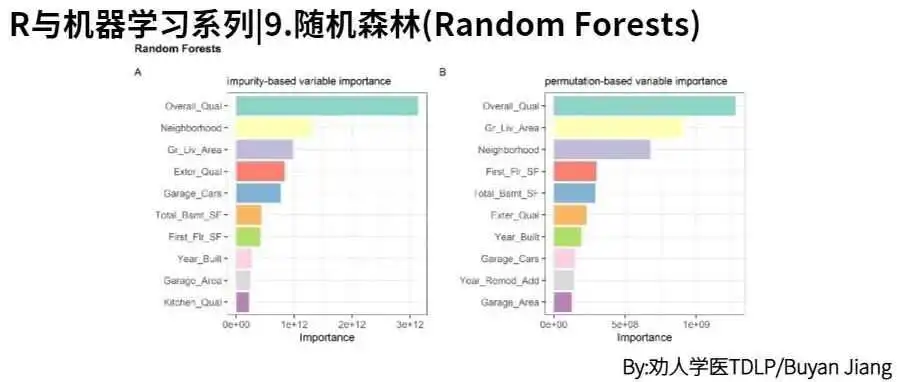
R与机器学习系列|9.随机森林(Random Forests)

R与机器学习系列|10.梯度提升算法(Gradient Boosting)（一）

到此这篇梯度提升树算法流程图（梯度提升树分类算法）的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章，希望大家都能在编程的领域有一番成就！

上一篇：梯度提升决策树原理（梯度提升决策树简介）

下一篇：没有了

版权声明：
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/jszy-jnts/83173.html

相关文章：