基于四元sigmoid激活函数的图像分类方法及系统
技术领域
1.本发明涉及深度学习技术领域,特别是涉及一种基于四元sigmoid激活函数的图像分类方法及系统。
背景技术:
2.近年来深度学习以其强大的性能优势在图像处理领域逐渐替代了传统算法成为主流方法。伴随着大量研究人员的大量实验,有研究人员发现实数域的神经网络不能很好的保存高维信息导致出现性能瓶颈。四元数由于其天生具备处理高维信息的能力逐渐被更多研究人员所关注。因此将四元数应用到神经网络,得到四元神经网络是一个很重要的课题。
3.四元数的运算法则使四元数不是四个分量的简单组合,而是一个高维信息的整体。其作为一个整体,分量与分量之间相互关联,分量之间的联系里也保存有数据的信息。rgb彩色图像像素点的数据格式与四元数的数据相似,每个像素都是由r、g、b三元色的分量组成。所以出现很多使用四元数来表征像素信息,即使用四元数矩阵来表示彩色图像并进行图像处理。使用四元数表示的图像数据,其颜色分量之间也相互关联保存有图像的信息,如不遵守四元数的运算法则,将造成图像数据在图像处理过程中的丢失。因此有必要在使用四元数表示图像进行图像处理过程中遵循四元数的运算法则,保留数据信息的完整性。
4.现有的利用四元数进行图像处理的方法,大多是把表征像素信息的四元数看作四个分量(一个实部与三个虚部)的简单相加。计算四元数的激活函数,首先把一个完整的四元数分裂为四个实部,然后把每个实部分别输入到实数的激活函数得到各个分量的输出,最后再将每个输出拼凑回到一起还原回四元数的形式。这种方法没有考虑到使用四元数表示的图像数据,其颜色分量之间也相互关联,并保存有图像的信息,从而造成在图像处理过程中丢失了一些图像数据。
5.因此,本领域亟需一种遵循四元数的运算法则,保留图像数据信息完整性的技术方案。
技术实现要素:
6.本发明的目的是提供一种基于四元sigmoid激活函数的图像分类方法及系统,其能够遵循四元数运算法则,并满足深度学习反向传播的可微分条件,从而保留了图像数据信息的完整性,提高了图像分类的准确性,有效解决了现有技术中将四元数拆分为四个分量单独处理,不能把通道间的信息有效的利用起来的问题。
7.为实现上述目的,本发明提供了如下方案:
8.一种基于四元sigmoid激活函数的图像分类方法,所述方法包括:
9.获取待分类图像;
10.利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;
11.所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;
12.所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。
13.在一些实施例中,所述四元激活函数为:q=qa+qbi+qcj+qdk
14.其中,q表示四元图像特征信息,qa表示四元图像特征信息的实部分量;qb表示四元图像特征信息虚部i的分量;qc表示四元图像特征信息虚部j的分量,qc表示四元图像特征信息虚部k的分量;
15.所述四元激活函数中四元数的除法计算公式为:
16.在一些实施例中,在所述获取待分类图像之后,还包括:
17.将所述待分类图像进行取均值和方差归一化处理,并调整为32x32大小的rgb图。
18.在一些实施例中,所述基于四元sigmoid激活函数的图像分类网络的训练过程,具体包括:
19.获取训练图像;
20.利用四元卷积层提取所述训练图像的四元图像特征信息;
21.将所述四元图像特征信息分别输入四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路利用四元激活函数对所述四元图像特征信息进行前向传播计算后,再进行卷积操作,得到四元激活处理数据;所述卷积支路对所述四元图像特征信息进行卷积操作,得到卷积处理数据;
22.将所述四元激活处理数据和所述卷积处理数据按四元特征矩阵形式拼接,得到四元特征矩阵;
23.对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵;
24.利用全连接层根据所述归一化四元特征矩阵计算图像分类的概率,得到网络输出向量;
25.利用交叉熵损失函数计算所述网络输出向量与真实标签的损失值;
26.结合所述损失值进行反向传播,并更新网络参数,得到基于四元sigmoid激活函数的图像分类网络。
27.在一些实施例中,在所述对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵之后,还包括:
28.利用四元池化层对所述归一化四元特征矩阵进行池化操作,得到池化四元特征矩阵;
29.对所述池化四元特征矩阵依次进行卷积操作、批量归一化操作和relu激活函数操
作。
30.在一些实施例中,所述四元激活函数为:q=qa+qbi+qcj+qdk
31.其中,q表示四元图像特征信息,qa表示四元图像特征信息的实部分量;qb表示四元图像特征信息虚部i的分量;qc表示四元图像特征信息虚部j的分量,qc表示四元图像特征信息虚部k的分量;
32.所述四元激活函数中四元数的除法计算公式为:
33.在一些实施例中,在所述获取训练图像之后,还包括:
34.对所述训练图像进行取均值、方差归一化操作,并调整所述训练图像的大小为32x32的3通道rgb图像。
35.在一些实施例中,所述利用四元卷积层提取所述训练图像的四元图像特征信息,具体包括:
36.对所述训练图像进行步长为1的卷积操作,得到一维四元特征矩阵;
37.利用四元卷积层提取所述一维四元特征矩阵的四元图像特征信息;所述四元卷积层的卷积核大小为3x3、特征边缘填充为1、步长为1以及四元卷积核为32。
38.在一些实施例中,在所述利用四元卷积层提取所述训练图像的四元图像特征信息之后,还包括:
39.将所述四元图像特征信息的每个通道特征数据进行去均值和方差归一化操作。
40.本发明还提供了一种基于四元sigmoid激活函数的图像分类系统,所述系统包括:
41.图像获取单元,用于获取待分类图像;
42.图像分类单元,用于利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;
43.所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;
44.所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。
45.根据本发明提供的具体实施例,本发明公开了以下技术效果:
46.本发明提供了一种基于四元sigmoid激活函数的图像分类方法及系统,首先,获取待分类图像;然后,利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据
和所述四元卷积处理数据按四元特征矩阵形式拼接。由于本发明利用四元sigmoid激活函数和与之配合的并联结构,使得本发明能够遵循四元数运算法则,并满足深度学习反向传播的可微分条件,从而保留了图像数据信息的完整性,提高了图像分类的准确性,有效解决了现有技术中将四元数拆分为四个分量单独处理,不能把通道间的信息有效的利用起来的问题,同时由于本发明提出了与其配套的并联网络结构,使整体系统可以快速收敛达到最优的结果。
附图说明
47.为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
48.图1为本发明提供的sigmoid函数图像。
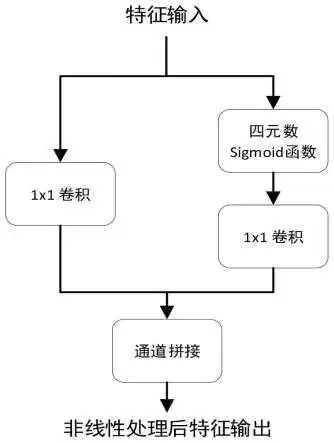
49.图2为本发明提供的四元sigmoid激活函数并联结构示意图。
50.图3为本发明实施例一提供的基于四元sigmoid激活函数的图像分类方法流程图。
51.图4为本发明实施例一提供的基于四元sigmoid激活函数的图像分类网络的网络模型示意图。
52.图5为本发明实施例一提供的四元sigmoid激活函数结构的使用方法示意图。
53.图6为本发明实施例一提供的基于四元sigmoid激活函数的图像分类网络训练流程图。
54.图7为本发明实施例一提供的无并联结构的网络模型示意图。
55.图8为本发明实施例一提供的识别准确率示意图。
56.图9为本发明实施例二提供的基于四元sigmoid激活函数的图像分类系统的框图。
具体实施方式
57.下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
58.近年来深度学习以其强大的性能优势在图像处理领域逐渐替代了传统算法成为主流方法。伴随着大量研究人员的大量实验,有研究人员发现实数域的神经网络不能很好的保存高维信息导致性能瓶颈。四元数由于其天生具备处理高维信息的能力逐渐被更多研究人员所关注。因此将四元数应用到神经网络,得到四元神经网络是一个很重要的课题。
59.四元数数由w.r.hamilton于1843年发明,它是一个关联的非交换四维代数[1]。四元数如下所示,一个完整的四元数由一个实部和三个虚部构成。
[0060]
q=qa+qbi+qcj+qdk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1.1)
[0061]
所使用符号定义:q表示四元数;qa为四元数实部分量;qb为四元数虚部i的分量;qc为四元数虚部j的分量;qd为四元数虚部k的分量。
[0062]
其中正交的虚数单位i,j,k遵循以下规则:
[0063]
i2=j2=-1,k=ij=-ji
→
k2=-1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1.2)
[0064]
从上式的运算法则中可以看出,四元数的运算法则使四元数不是四个分量的简单组合,而是一个高维信息的整体。其作为一个整体,分量与分量之间相互关联,分量之间的联系里也保存有数据的信息。rgb彩色图像像素点的数据格式与四元数的数据相似,每个像素都是由r、g、b三元色的分量组成。所以出现很多使用四元数来表征像素信息,即使用四元数矩阵来表示彩色图像并进行图像处理。使用四元数表示的图像数据,其颜色分量之间也相互关联保存有图像的信息,如不遵守四元数的运算法则,将造成图像数据在图像处理过程中的丢失。因此有必要在使用四元数表示图像进行图像处理过程中遵循四元数的运算法则,保留数据信息的完整性。
[0065]
现有的研究人员通过将四元数与深度学习算法相结合,改进得到四元数卷积运算、四元数池化层等组件,提出了不同的四元数神经网络。比较经典的是quaternion convolutional neural network for color image classification and forensics这篇论文提出了一套相对完备的四元数神经网络组件。这篇论文将四元数乘法转为卷积运算得到四元数卷积层,提出四元数各分量的平方和作为指导矩阵的四元数池化层。在非线性部分即激活函数上为了简化计算,避开四元数函数的解析性问题,该方法将完全四元数分成四个实数,分别用实数函数相运算,然后求和得到输出。如下式(2.1)所示
[0066]
f(q)=f(qa)+f(qb)i+f(qc)j+f(qd)k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2.1)
[0067]
(注:上述公式的f(
·
)表示的是任意的标准实数激活函数,q表示为四元数)
[0068]
本方法的主要技术方案是将组成四元的四个分量分别输入到激活函数(该文中使用的是relu激活函数),计算得到每个分量输出后再将各个分量组合还原为四元数形式。
[0069]
上文提出的激活函数方法,把四元数看作四个分量(一个实部与三个虚部)的简单相加。计算四元数的激活函数,首先把一个完整的四元数分裂为四个实部,然后把每个实部分别输入到实数的激活函数得到各个分量的输出,最后再将每个输出拼凑回到一起还原回四元数的形式。
[0070]
尽管这样设计的输入与输出看起来就是一个四元数的非线性层,但深究其设计原理会发现这个方法的设计存在一些不足之处:
[0071]
四元数作为一个整体,其包含的信息不仅仅是各个分量的简单和,其通道之间也有很大的相关信息。该方法将四元数拆分为四个分量单独处理,没有把通道间的信息有效的利用起来。
[0072]
神经网络的反向传播更新网络参数的过程需要使用四元数的一阶微分信息。四元数作为一种超复数,需要使用微分偏导数自然也要满足复数的可微分的条件。而该方法的设计中没有考虑和解决这一问题。
[0073]
综上所述,该论文提出的关于四元数神经网络的激活函数没有遵守四元数运算的规则,只是在形式上完成了类似四元数运算的操作。基于以上问题本发明将致力于完成以下的任务:
[0074]
设计一个对完整四元数进行处理的四元激活函数,使其能够获取四元数中包含的所有信息。
[0075]
设计一个能够满足四元数可解析性条件的函数,是其能够在理论和实践上完成网络的方向传播和误差的梯度下降。
[0076]
在研究了现有方法的优缺点和研究目的后,本发明提出了一种常用非线性函数的四元数形式下的激活函数,使其能够遵循四元数运算法则的情况下,满足深度学习反向传播的可微分条件。并且设计与其配套的网络结构,使整体系统可以快速收敛达到最优的结果。整个系统的设计基于图像分类应用邻域,发明旨在提升四元数神经网络在图像分类任务上的准确性。
[0077]
为了整体处理四元数,就需要使用到四元数函数。而要把四元数函数应用到神经网络就要满足可解析性。四元数的全局可解析性条件由柯西黎曼富特(cauchy-riemann-fueter,crf)给出,如式4.1所示。
[0078][0079]
其中,f(q)表示含四元数q的函数,表示f(q)对
·
求偏导数。
[0080]
这个常用的全局可解析性条件由于太过与严格,基本只有线性函数才能满足这一条件。导致四元非线性函数的发展受到极大的限制。
[0081]
尽管神经网络需要的就是四元非线性函数,这不能满足crf的全局可解析性,但是神经网络反向传播更新参数所需要的只是局部可解析性。为了证明四元数局部可解析性,提出了一个宽松的crf条件,如式4.2所示
[0082][0083]
其中定义数学量虚数单位与单位量α的表达式如下:
[0084][0085]
这里所提到的局部是以虚数单位附近的一阶可微性。刚好梯度下降方法只需要在一点附近的偏微分,所以这个条件适用于神经网络更新参数的偏微分证明。
[0086]
本发明将使用实值神经网络中常用的激活函数——sigmoid激活函数。表达式见式4.4.
[0087][0088]
其函数图像如图1所示。
[0089]
sigmoid函数的优点有:
[0090]
sigmoid函数在其定义域内处处可微分,没有不可微分的奇点。这有利于图像分类任务中,神经网络的参数利用微分的梯度下降参数更新
[0091]
sigmoid函数使用广泛,其实际应用价值得到了众多实践的验证,在图像分类中得到广泛应用。
[0092]
sigmoid函数能压缩数据并保持信号的幅值,这使得网络可以将特征的数值控制在较为合理的范围,有利于高阶特征的保留与网络训练结果的收敛。
[0093]
综合以上的优点可以得出sigmoid函数自身的特性使其可以很好的应用于图像分类任务。
[0094]
由公式4.4可以看出sigmoid函数是由四元指数函数构成的。复数域的四元指数函数并不简单,由于四元数乘积的不可交换性,四元数指数函数存在几种定义,为了方便考虑使用以下指数函数的定义,如式4.5所示。
[0095][0096]
其中eq表示以自然数e为底的四元指数函数式。
[0097]
根据欧拉公式又可表示如式4.6:
[0098][0099]
其中的α和由式4.3给出。经过推算得到:
[0100][0101]
可得出四元指数函数满足局部可解析的宽松crf条件。
[0102]
四元指数函数的微分如式4.8所示
[0103][0104]
本发明设计四元激活函数为:
[0105][0106]
四元数的除法运算定义如下:
[0107][0108]
四元数sigmoid激活函数的局部可解析证明:
[0109]
根据多元函数微分的链式求导法则可得
[0110][0111]
将公式4.9代入公式4.11可得到
[0112][0113]
即本发明提出的四元数sigmoid激活函数满足局部可解析的宽松crf条件。
[0114]
四元激活函数的微分推导:
[0115][0116]
将式4.8代入到式4.13可以得到四元sigmoid激活函数的微分为:
[0117][0118]
经过上述的证明和推导,可得本发明所提出的四元数sigmoid激活函数满足局部可解析性条件。同时也满足了对四元数进行整体处理设计目的,这使得特征的通道间信息得到很好的保留,特征信息越多越完整就可以提升网络在图像分类上的准确性。
[0119]
同时,考虑到sigmoid函数相比常用的relu激活函数会出现梯度消失和梯度爆炸的问题,导致网络训练难以继续。为了解决这一问题,本发明提出了一种四元sigmoid激活函数结构,原理如下:
[0120]
神经网络本质上是利用梯度下降降低损失函数,从而将网络学习为一个由输入数据经过处理对应到输出数据的高维映射如公式4.15所示。
[0121]fr
:a
→
b(4.15)
[0122]
这里令fr为由输入数据集a到数据集b的映射,设其为将a投影到m维度上的映射。映射的维度在定义网络结构的时候以及初步确定,如果在定义网络的时候定义出一个将输入数据集a投影到n维的映射f,当n》》m时需要通过参数学习的方式将网络映射维度降低。这将会给网络训练带来麻烦。为了避免这一问题在经典网络resnet中提出了跳接结构,通过并联跳接的方法使网络可以更加容易的学习到0~n维的映射。
[0123]
考虑到sigmoid相比常用relu会极大的提升网络的非线性表达能力,为了使这一能力在学习过程中更加可控,本发明提出了针对激活函数的并联跳接。并且为了让网络更好的选择跳接还是激活函数占比更大权重,在两条支路后面分别并联了一个卷积核为1x1大小的卷积层作为一个权重的选择,最后将两条支路的输出在通道维度上进行拼接得到输出。
[0124]
最后本发明提出如图2所示的多路并联结构配合四元数sigmoid函数使用。输入的变量同时输入到1x1支路和四元sigmoid激活函数支路,使用1x1卷积的作用是作为权重使用,由学习过程来调整两条支路前向传播的权重大小。在计算得到两条支路的输出后,在通道维度上将数据拼接得到输出。
[0125]
本发明的目的是提供一种基于四元sigmoid激活函数的图像分类方法及系统,其能够遵循四元数运算法则,并满足深度学习反向传播的可微分条件,从而保留了图像数据信息的完整性,提高了图像分类的准确性,有效解决了现有技术中将四元数拆分为四个分量单独处理,不能把通道间的信息有效的利用起来的问题。
[0126]
为使本发明的上述目的、特征和优点能够更加明显易懂,下面结合附图和具体实施方式对本发明作进一步详细的说明。
[0127]
实施例一:
[0128]
如图3所示,本实施例提供了一种基于四元sigmoid激活函数的图像分类方法,所述方法包括:
[0129]
s1、获取待分类图像。
[0130]
然后,将所述待分类图像进行取均值和方差归一化处理,并调整为32x32大小的rgb图。
[0131]
s2、利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;
[0132]
所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;
[0133]
所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。其中,所示四元特征矩阵指的是利用四元卷积层提取的利用四元数表示的图像的特征信息。
[0134]
所述四元激活函数为:q=qa+qbi+qcj+qdk
[0135]
其中,q表示四元图像特征信息,qa表示四元图像特征信息的实部分量;qb表示四元图像特征信息虚部i的分量;qc表示四元图像特征信息虚部j的分量,qc表示四元图像特征信息虚部k的分量;
[0136]
所述四元激活函数中四元数的除法计算公式为:
[0137]
本发明的主要技术就是通过设计符合四元数运算的sigmoid函数非线性层结构并将其应用到图像分类的四元数网络结构中,使其增强网络的数据处理能力提升图像分类的识别准确度。
[0138]
本实施例中,四元神经网络结构(基于四元sigmoid激活函数的图像分类网络)设计如下:
[0139]
利用传统的四元神经网络组件:四元卷积操作、四元池化操作、批量归一化、全连接层、激活函数层,组件四元数神经网络。读取预处理后的彩色图像作为网络的输入数据,首先是使用一个简单的卷积层将输入的三维输入数据转为符合四元数表示的四维数据。而后经过四元卷积层、池化层、批量归一化等一系列交替进行的特征提取操作得到输入图像的特征信息。最后使用全连接层将所有的特征信息融合,输出得到图像经过网络计算后得到的图像被分类为每个类别的概率(此处的“概率”非真正意义上的数学概率,而是研究人员对网络输出数据的物理量的一种解释。本质就是网络输出的数据),找出概率最大的类别即图像的分类类别。由于本实施例实验使用的数据集中有飞机、汽车、鸟类、猫、鹿、狗、蛙类、马、船和卡车等10个类别的图像,因此最后一个全连接层的输出设置为10,这10个数的意思是输入图像被网络分类为飞机、汽车、鸟类等这10个数据集图像类别的概率大小,输出的值越大被分为该类别的可能性就越大。在网络的训练过程中就是使图像经过网络计算为正确类别的那个数越大,而被判定为其它图像类别概率的值越小。最终使用网络时,网络的图像分类输出选取全连接层输出10个数的最大值为网络类别输出。具体的网络结构如图4所示。图4中,四元数卷积层的“k(3x3)p1 s1”,其中“k(3x3)”表示卷积核的大小是3x3大小;“p1”表示卷积的特征填充为1;“s1”表示卷积的步长为1。连接线上的数字表示特征的维度,其表示方式为width
×
height
×
(channel)。其中的卷积都使用四元数卷积,同时使用四元数池化层。根据实验数据来看,由于使用四元数的批量归一化处理和全连接层不是必要的。因此为了方便,本实施例使用常用的实数域的批量归一化层和全连接层。
[0140]
将浅层四元网络的激活函数替换为图2所示的四元激活函数结构。本实施例设计的四元sigmoid激活函数结构的使用方法如图5所示。
[0141]
使用四元sigmoid激活函数并联结构的方法如下:
[0142]
首先通过在上文中提到的四元sigmoid函数层的式4.9实现四元sigmoid的前向传播计算、式4.14实现四元sigmoid反向传播计算,式4.10提供了便于使用程序实现前向传播与反向传播计算中的四元数除法运算。在得到四元sigmoid函数组件后搭建图2所示的激活函数并联结构。
[0143]
与使用普通relu激活函数分别对每个四元分量进行相同的非线性处理的方法有所区别的是:为了使本实施例的输入输出与传统的relu激活函数的输入输出接口一致(传统relu激活函数的输入是一个完整的四元sigmoid多通道特征数据,输出是一个经过非线性处理的完整四元sigmoid多通道特征数据),本实施例的激活函数层需要在非线性处理前提取出各个四元分量,在并联支路的数据拼接时需要把四元分量相对应的拼接。细节如下:
[0144]
四元激活层的输入是一个按一个实部分量多通道数据与三个虚部多通道矩阵拼接的四元特征矩阵(与rgb彩色图像的存储类似,图像的每个像素点级别的特征信息都是由一个四元数所表示,图像是二维平面的信息所以用四元矩阵表示一张图像。但因为计算机目前没有直接的四元数的存储类型,所以都是把qa,qb,qc,qd这四个分量在通道维度上拼接为一个多通道四元矩阵的形式存储四元数),计算四元sigmoid函数时需要把四元矩阵对应的实部qa与虚部qb,qc,qd各个分量按对应的通道位置(即把总通道数分四份,通道位序从低到高分别对应qa,qb,qc,qd的多维特征)分离开,从而计算前向传播与反向传播过程。在图2的结构之下,输入到非线性处理层(即激活函数层)的特征数据分别经过单1x1卷积运算支路和四元sigmoid激活函数串联1x1卷积支路得到两个四元数多通道数据。为了使输出为一个完整的四元数多通道数据,再将单1x1卷积运算支路和四元sigmoid激活函数串联1x1卷积支路的输出特征数据进行通道拼接时需要将两支路的四元输出按实部qa与虚部qb,qc,qd对应四元分量类型拼接。如此拼接即可使本实施例的四元sigmoid激活函数并联结构与传统relu激活函数层直接进行替换,无需改动网络其他结构。
[0145]
经过以上步骤就得到了一个完整的四元sigmoid激活函数并联结构层。使用时只需要将此结构替换原四元数网络的relu激活函数层,即可得到本实施例的基于四元sigmoid激活函数并联结构的深度学习网络。由于保证了本实施例与原网络激活函数层输入输出接口的一致,所以使用本实施例的四元sigmoid激活函数并联结构替换原网络的激活函数层时,没有位置与数量上的限制。
[0146]
本实施例中,基于四元sigmoid激活函数的图像分类网络的训练过程,具体包括:
[0147]
a1、获取训练图像。
[0148]
本实施例中用到的数据集采用经典的cifar10彩色图像10分类数据集。cifar10数据集由6万张32x32大小的rgb彩色图片组成,一共有10个类别。每个类别6000张图片。其中有5万张训练图片及1万张测试图片。
[0149]
然后对这些训练图像进行数据增强处理,通过对训练图像进行去均值、方差归一化调整图像大小为32x32的3通道rgb图像,最终实现的6000张去均值、方差归一化的彩色图像作为本实施例的训练数据。
[0150]
a2、利用四元卷积层提取所述训练图像的四元图像特征信息。
[0151]
本实施例对所述训练图像进行步长为1的卷积操作,得到一维四元特征矩阵;利用四元卷积层提取所述一维四元特征矩阵的四元图像特征信息;所述四元卷积层的卷积核大小为3x3、特征边缘填充为1、步长为1以及四元卷积核为32。最后将所述四元图像特征信息的每个通道特征数据进行去均值和方差归一化操作。
[0152]
a3、将所述四元图像特征信息分别输入四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路利用四元激活函数对所述四元图像特征信息进行前向传播计算后,再进行卷积操作,得到四元激活处理数据;所述卷积支路对所述四元图像特征信息进行卷积操作,得到卷积处理数据。
[0153]
a4、将所述四元激活处理数据和所述卷积处理数据按四元特征矩阵形式拼接,得到四元特征矩阵。
[0154]
a5、对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵。
[0155]
a6、利用全连接层根据所述归一化四元特征矩阵计算图像分类的概率,得到网络输出向量。
[0156]
作为一种具体的实施方式,本实施例中将训练数据集里的数据按随机的类别读取一批图像,同时对其进行取均值、方差归一化与调整图像大小为32x32的3通道rgb图像,并记录其对应的标签数据。
[0157]
将32x32的3通道图像输入到图像分类网络模型中。进入模型后,首先使用一个普通的1x1卷积核,步长为1的卷积操作,目的是调整通道维度为4,其分别匹配四元数的qa,qb,qc,qd四个分量。输出得到大小为32x32的4通道图像特征即一个完整的一维四元特征矩阵;接着输入到“卷积核大小为3x3、特征边缘填充为1、步长为1、四元卷积核32个”的四元卷积层提取四元图像特征信息,输出为32x32大小、维度为32的四元特征矩阵(一个维度的四元特征矩阵由于是有四个分量组成,每个分量都使用一个通道所表示。则“维度为32的四元特征矩阵”本质上是通道数为32x4=128的特征数据,四元矩阵分量的排列形式为前0~31通道为qa分量,32~63通道为qb分量,64~95通道为qc分量,96~127通道为qd分量,且每一分量内的通道序号相同的通道特征数据qa,qb,qc,qd分量为一个完整的四元特征矩阵);然后把32维的四元特征矩阵输入到批量归一化层,批量归一化层将每一通道特征数据做去均值、方差归一化的操作。目的是调整特征数据的分布,使其更平稳与集中便于卷积参数的学习过程,输出特征的大小与输入到批量归一化层的特征一致为32维32x32大小的四元特征矩阵。
[0158]
接下来就到了四元sigmoid激活函数并联结构,32维32x32大小的四元特征矩阵被分别输入到两条分支,一条是经四元sigmoid激活函数的前向传播计算式(式4.9、式4.10)计算后的得到的非线性处理后的数据,其输出为32维32x32的四元特征矩阵。
[0159]
[0160][0161]
其中,q表示四元图像特征信息,qa表示四元图像特征信息的实部分量;qb表示四元图像特征信息虚部i的分量;qc表示四元图像特征信息虚部j的分量,qc表示四元图像特征信息虚部k的分量。
[0162]
后面接一个“大小为1x1、步长为1、卷积核个数为16的”普通卷积操作,整个支路输出为32x32的16维四元特征矩阵。另一条支路为,与前一条支路的卷积一样的单1x1普通卷积操作,输出为32x32的16维四元特征矩阵。最后将两条支路的通道按四元特征矩阵形式拼接(将两条支路得到的两个完整的四元数特征矩阵按顺序分离各分量并按相同分量对应连接的方式进行通道数据的拼接,整个操作的数学表达式:输出其中,表示通道维度上的数据连接操作,以这种形式将两个四元矩阵拼接为一个完整的四元矩阵)得到32维32x32大小的四元特征矩阵。接着再将特征输入到“卷积核大小为3x3、特征边缘填充为1、步长为1、32个四元卷积核”的四元卷积层提取四元图像特征信息,输出为32x32大小、维度为32的四元特征矩阵;后面接批量归一化和relu激活函数层。这两个层的操作与前面一致,批量归一化是对输入到该层的特征数据进每一通道特征数据的均值、方差归一化的操作;relu激活函数层是将输入到该层的特征数据经过relu激活函数(relu激活函数公式:relu(input)=max(input,0),input表示输入数据;max(input,0)表示取0与input数据两者更大的值)的处理。目的也同前面的批量归一化和激活函数层,两层都不会改变输入特征矩阵的大小,输入特征数据与输出特征数据一致,输出仍然为32维32x32大小的四元特征矩阵。虽然特征数据的维度与大小没有变化,但此时的特征信息因为经过了更多的卷积层、批量归一化与激活函数层,特征矩阵已经包含了更多与更深层次的特征信息。
[0163]
然后把32维32x32大小的四元特征矩阵输入“大小为2x2、步长为2”的四元池化层。其目的为弱化特征受位置的影响,提高网络特征提取的性能。输出为32维16x16大小的四元特征矩阵。
[0164]
池化层输出后,再将特征数据输入到两条串联的“依次连接的卷积层、批量归一化、relu激活函数层”子网络单元,其中卷积层为64个大小为3x3、特征填充为1、步长为1的四元卷积核的卷积操作,目的是提取输入特征数据的深层次特征数据,输出得到64维16x16大小的深层次特征;批量归一化同样是通过对通道数据进行去均值与方差归一化得到数据分布集中在0附近且分布更均衡的特征数据;relu激活函数层是将数据经过relu激活函数处理,输出经过非线性处理的特征数据。两个“依次连接的卷积层、批量归一化、relu激活函数层”子网络单元的操作方法与目的都是一样的,输出都是64维16x16大小的四元特征矩阵。使用这样两个相同子网络串联的目的是通过加深网络的形式提取特征数据里更深层次的信息。更多更深层次的信息有利于提高网络对图像分类的准确率。然后再将特征输入到“大小为2x2、步长为2”的四元池化层,目的同样是为了提取显著特征,弱化特征受位置的影响,输出为64维8x8大小的四元特征矩阵。
[0165]
最后是将提取的特征输入到两层全连接层,其目的为整合前面卷积等操作提取的
特征用于图像分类,使用两层是为了增加全连接层的深度增强其处理特征的能力。前一层的全连接层输入大小为输入特征数据的大小为8x8x64x4=16384,输出数据大小与全连接层的节点数相同,在此设置为512。如此经前一全连接层的计算,输入的64维8x8大小的四元特征矩阵,输出得到长度为512的一维特征向量。后一层的输入为长度512的一维特征向量,输出为与数据集图像类别一致的长度为10的向量(网络输出向量)。这10个数的意义普遍被解释为输入图像经过网络计算预测为10个(按“0:飞机,1:汽车,2:鸟,3:猫,4:鹿,5:狗,6:蛙,7:马,8:船,9:卡车”的固定位序排列的)图像类别的“概率”(此处的“概率”非真正意义上的数学概率,而是研究人员对网络输出数据的物理量的一种解释。其意义与数学的概率的物理意义相似,且存在正相关。数值越大代表输入图像被网络预测为该类别的可能性就越大)。
[0166]
a7、利用交叉熵损失函数计算所述网络输出向量与真实标签的损失值。
[0167]
本实施例中,得到长度为10的网络输出向量后,按交叉熵损失函数(公式为:其中m表示数据集的类别;pc为网络输出向量的第c个数的值;yc为符号函数,当c与该图像的真实类别一致时为“1”否则为“0”)计算网络输出向量与其对应图像的真实类别向量(其中一个真实标签位置数值为1,其余九个标签位置为0)的损失值。至此得到整个网络训练的前向传播过程。
[0168]
a8、结合所述损失值进行反向传播,并更新网络参数,得到基于四元sigmoid激活函数的图像分类网络。
[0169]
得到网络的“前向传播”过程后,延其计算过程的“计算图”从“损失值”开始计算网络中每个参数的梯度,这一过程称作“反向传播”,主要是计算梯度。利用链式求偏导数的方法计算得到损失值对每一个网络参数的偏导数即梯度值,在链式计算至sigmoid激活函数时,通过式4.14的公式可以计算得到反向输入的导数对每个四元参数分量的偏导数(梯度)。由于训练网络的目的是降低网络计算的损失值,所以网络参数的更新方向为网络参数对损失值梯度的相反方向。本实施例具体使用adam算法更新网络参数。
[0170]
重复以上步骤a1到a8,直到网络的分类计算性能达到最高即损失值与分类准确率收敛。此时认为网络训练结束,连同网络参数保存网络模型。确认收敛的动作一般是人为完成的,比如说训练80轮准确率到了90%且连续若干轮周期都没有大的变化了,就认为收敛了。并且一般还会多训练几轮。
[0171]
神经网络训练的总体流程如下图6所示。通过输入训练图像及其对应的图像类别来训练网络参数,使用网络的反向传播计算网络参数更新时需要的梯度。网络训练的目的是使网络经过若干轮的网络损失值的梯度下降后,输出一个可以使网络识别准确率高的一整套网络模型对应的网络参数。经实验得到,在100个迭代周期内网络可以收敛,所以指定训练迭代周期为100。
[0172]
本实施例中使用该模型的一般步骤包括:
[0173]
步骤一:将读取到的图像进行取均值、方差归一化、调整图像大小为32x32大小的rgb图。
[0174]
步骤二:读取在训练阶段完成训练的网络模型及其对应的网络参数。
[0175]
步骤三:将步骤一输出的图像输入到网络计算,得到图像被分类为10个类别的概
率值。
[0176]
步骤四:选取网络计算概率值最大的类别作为图像的分类类别。至此便完成了使用网络对图像分类的任务。
[0177]
为了更有力的证明本实施例的效果,设计了六组对照实验组如下表1所示:
[0178]
表1实验对照组设置表
[0179][0180]
对于含并联结构的实验组1、2、3,网络模型如图4所示。不同实验组只需要改变图一所示结构中的激活函数即可。
[0181]
对于不含并联结构的实验组4、5、6,网络模型如图7所示。为了保证模型参数的一致性,排除产数量变化引起的模型不同,选择在激活函数模块后加了一层1
×
1卷积层。
[0182]
所有的实验组都使用梯度下降算法使用目前使用广泛的adam梯度下降学习算法。学习率设置为0.0005,并且使用余弦退火学习率衰减策略,设置余弦周期为一轮网络训练周期。使用交叉熵损失函数作为代价函数。
[0183]
实验平台:
[0184]
硬件平台:gpu:titan xp显存:12gb
[0185]
cpu:7核intel(r)xeon(r)cpu e5-2680 v4内存:16gb
[0186]
软件平台:pytorch:1.7.0python 3.8cuda 11.0
[0187]
经过多次实验选出准确率最高的作为最终结果,绘制其模型在测试数据集上的准确率如图8所示。
[0188]
从图8中可以看出,本实施例提出的四元数sigmoid激活函数(即实验1)结构取得了最高的识别准确率,性能最佳。提取出整个学习过程中最高的识别最缺率,得到如下表的结果:
[0189]
表2网络实验结果
[0190][0191]
由实验1、2、3比较可得出在相同的并联结构网络模型下本实施例的四元数激活函数表现好,使网络表现出了更好的泛化能力。由实验1、4的比较可得出本实施例所提出的并联结构很好的克服了sigmoid函数不好训练的缺点,增强了网络对不同维度数据分布的表现能力。
[0192]
本实施例提供了一种基于四元sigmoid激活函数的图像分类方法,首先,获取待分类图像;然后利用四元sigmoid激活函数图像分类网络对待分类图像进行图像分类;其中四
元sigmoid激活函数图像分类网络包括并联结构层;所述并联结构层包括并联的四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;并将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。通过分析四元数指数函数,结合常用的sigmoid实值激活函数,得到四元数sigmoid激活函数。利用宽松的lac条件,论证了常用非线性激活函数对应四元数表示下的四元sigmoid函数的局部可解析性。推导了四元数sigmoid函数的微分导数,并将其用于神经网络的反向传播过程更新参数。结合跳接与inception结构提出了适合四元数sigmoid激活函数的并联结构,提升网络对不同维度图像的表现能力。其提出了四元数非线性激活函数,丰富了四元数神经网络在激活函数方面的设计组件。根据满足宽松crf条件的四元函数,提出了有局部可解析性的可对四元数数据整体处理的函数。通过计算推导,得到其局部解析性,并将其应用到四元数激活函数的梯度下降算法。四元激活函数的并联结构提升了网络的泛化能力,抑制网络过拟合,极大的提升网络对不同维度数据的表现能力,从而提升四元数神经网络的性能。由于本发明利用四元sigmoid激活函数和与之配合的并联结构,使得本发明能够遵循四元数运算法则,并满足深度学习反向传播的可微分条件,从而保留了图像数据信息的完整性,提高了图像分类的准确性,有效解决了现有技术中将四元数拆分为四个分量单独处理,不能把通道间的信息有效的利用起来的问题,同时由于本发明提出了与其配套的并联网络结构,使整体系统可以快速收敛达到最优的结果。
[0193]
实施例二:
[0194]
如图9所示,本实施例提供了一种基于四元sigmoid激活函数的图像分类系统,所述系统包括:
[0195]
图像获取单元m1,用于获取待分类图像;
[0196]
图像分类单元m2,用于利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;
[0197]
所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;
[0198]
所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。
[0199]
该系统还包括:网络训练模块,用于:
[0200]
获取训练图像;
[0201]
利用四元卷积层提取所述训练图像的四元图像特征信息;
[0202]
将所述四元图像特征信息分别输入四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路利用四元激活函数对所述四元图像特征信息进行前向传播计算后,再进行卷积操作,得到四元激活处理数据;所述卷积支路对所述四元图像特征信息进行卷积操作,得到卷积处理数据;
[0203]
将所述四元激活处理数据和所述卷积处理数据按四元特征矩阵形式拼接,得到四元特征矩阵;
[0204]
对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵;
[0205]
利用全连接层根据所述归一化四元特征矩阵计算图像分类的概率,得到网络输出向量;
[0206]
利用交叉熵损失函数计算所述网络输出向量与真实标签的损失值;
[0207]
结合所述损失值进行反向传播,并更新网络参数,得到基于四元sigmoid激活函数的图像分类网络。
[0208]
本说明书中各个实施例采用递进的方式描述,每个实施例重点说明的都是与其他实施例的不同之处,各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言,由于其与实施例公开的方法相对应,所以描述的比较简单,相关之处参见方法部分说明即可。
[0209]
本文中应用了具体个例对本发明的原理及实施方式进行了阐述,以上实施例的说明只是用于帮助理解本发明的方法及其核心思想;同时,对于本领域的一般技术人员,依据本发明的思想,在具体实施方式及应用范围上均会有改变之处。综上所述,本说明书内容不应理解为对本发明的限制。
技术特征:
1.一种基于四元sigmoid激活函数的图像分类方法,其特征在于,所述方法包括:获取待分类图像;利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。2.根据权利要求1所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,所述四元激活函数为:q=q
a
+q
b
i+q
c
j+q
d
k其中,q表示四元图像特征信息,q
a
表示四元图像特征信息的实部分量;q
b
表示四元图像特征信息虚部i的分量;q
c
表示四元图像特征信息虚部j的分量,q
c
表示四元图像特征信息虚部k的分量;所述四元激活函数中四元数的除法计算公式为:3.根据权利要求1所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,在所述获取待分类图像之后,还包括:将所述待分类图像进行取均值和方差归一化处理,并调整为32x32大小的rgb图。4.根据权利要求1所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,所述基于四元sigmoid激活函数的图像分类网络的训练过程,具体包括:获取训练图像;利用四元卷积层提取所述训练图像的四元图像特征信息;将所述四元图像特征信息分别输入四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路利用四元激活函数对所述四元图像特征信息进行前向传播计算后,再进行卷积操作,得到四元激活处理数据;所述卷积支路对所述四元图像特征信息进行卷积操作,得到卷积处理数据;将所述四元激活处理数据和所述卷积处理数据按四元特征矩阵形式拼接,得到四元特征矩阵;对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵;利用全连接层根据所述归一化四元特征矩阵计算图像分类的概率,得到网络输出向量;利用交叉熵损失函数计算所述网络输出向量与真实标签的损失值;结合所述损失值进行反向传播,并更新网络参数,得到基于四元sigmoid激活函数的图
像分类网络。5.根据权利要求4所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,在所述对所述四元特征矩阵进行批量归一化和relu激活函数操作,得到归一化四元特征矩阵之后,还包括:利用四元池化层对所述归一化四元特征矩阵进行池化操作,得到池化四元特征矩阵;对所述池化四元特征矩阵依次进行卷积操作、批量归一化操作和relu激活函数操作。6.根据权利要求4所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,所述四元激活函数为:q=q
a
+q
b
i+q
c
j+q
d
k其中,q表示四元图像特征信息,q
a
表示四元图像特征信息的实部分量;q
b
表示四元图像特征信息虚部i的分量;q
c
表示四元图像特征信息虚部j的分量,q
c
表示四元图像特征信息虚部k的分量;所述四元激活函数中四元数的除法计算公式为:7.根据权利要求4所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,在所述获取训练图像之后,还包括:对所述训练图像进行取均值、方差归一化操作,并调整所述训练图像的大小为32x32的3通道rgb图像。8.根据权利要求4所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,所述利用四元卷积层提取所述训练图像的四元图像特征信息,具体包括:对所述训练图像进行步长为1的卷积操作,得到一维四元特征矩阵;利用四元卷积层提取所述一维四元特征矩阵的四元图像特征信息;所述四元卷积层的卷积核大小为3x3、特征边缘填充为1、步长为1以及四元卷积核为32。9.根据权利要求4所述的基于四元sigmoid激活函数的图像分类方法,其特征在于,在所述利用四元卷积层提取所述训练图像的四元图像特征信息之后,还包括:将所述四元图像特征信息的每个通道特征数据进行去均值和方差归一化操作。10.一种基于四元sigmoid激活函数的图像分类系统,其特征在于,所述系统包括:图像获取单元,用于获取待分类图像;图像分类单元,用于利用基于四元sigmoid激活函数的图像分类网络对所述待分类图像进行图像分类;所述基于四元sigmoid激活函数的图像分类网络包括并联结构层;所述并联结构层包括:拼接层、四元sigmoid激活函数支路和卷积支路;所述四元sigmoid激活函数支路和所述卷积支路并联;所述四元sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作,得到四元特征激活处理数据;所述卷积支路对四元特征矩阵进行卷积操作,得到四元卷积处理数据;所述拼接层将所述四元特征激活处理数据和所述四元卷积处理数据按四元特征矩阵形式拼接。
技术总结
本发明涉及一种基于四元Sigmoid激活函数的图像分类方法,属于深度学习技术领域,利用基于四元Sigmoid激活函数的图像分类网络对待分类图像进行图像分类。该图像分类网络包括并联结构层;并联结构层包括:拼接层、四元Sigmoid激活函数支路和卷积支路;其中四元Sigmoid激活函数支路和卷积支路并联;四元Sigmoid激活函数支路利用四元激活函数对四元特征矩阵进行前向传播计算后,再进行卷积操作;卷积支路对四元特征矩阵进行卷积操作;拼接层将两个输出拼接。本发明利用四元Sigmoid激活函数和与之配合的并联结构,能够遵循四元数运算法则,从而保留了图像数据信息的完整性,提高了图像分类的准确性。提高了图像分类的准确性。提高了图像分类的准确性。
技术研发人员:
盖杉 態页鹤
受保护的技术使用者:
南昌航空大学
技术研发日:
2022.09.05
技术公布日:
2022/12/1
到此这篇sigmoid函数导数形式(sigmoid函数计算公式)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/haskellbc/43823.html
