# 1. 激活函数概述
在深度学习模型中,激活函数的作用至关重要,它为神经网络引入非线性因素,使得网络能够学习和模拟复杂的数据特征。理解激活函数是构建有效神经网络的基础,也是优化和调试模型的关键。本章节将对激活函数的概念、目的和基本特性进行简要介绍,并探讨其在不同应用中的影响。
接下来的章节将深入探讨各类激活函数的具体应用,以及它们在实践中的优缺点,以帮助读者根据不同的网络结构和应用场景,选择合适的激活函数,提升模型性能。
# 2. Sigmoid激活函数
2.1 Sigmoid函数理论基础
2.1.1 Sigmoid函数的定义
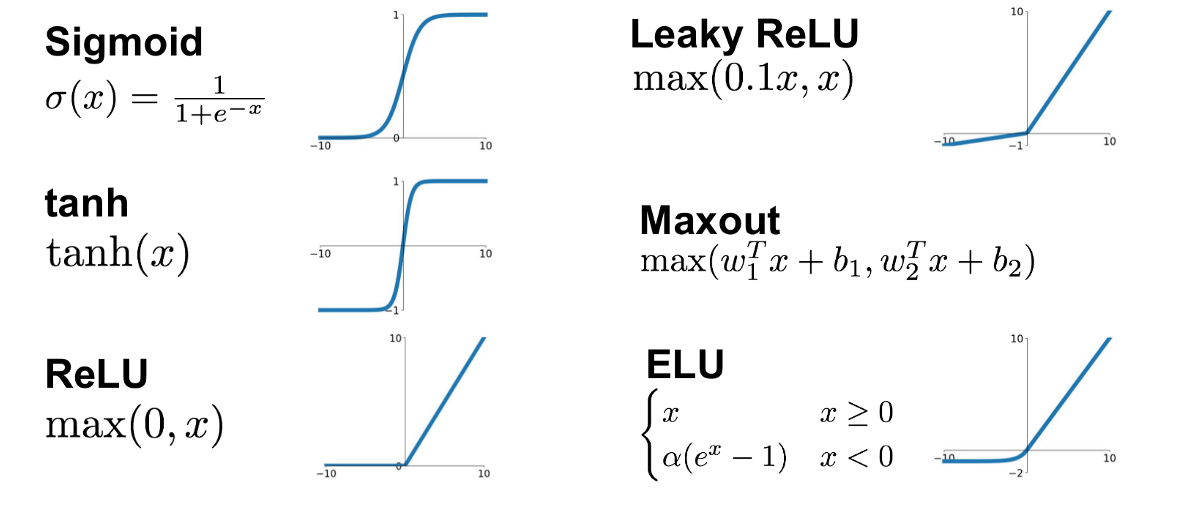
Sigmoid函数是一种广泛应用于神经网络的激活函数,它将任何实数值压缩至0和1之间。数学上,Sigmoid函数通常表示为:
f(x) = frac{1}{1 + e^{-x}}
这里,( e )是自然对数的底数,约为2.71828。Sigmoid函数的输出可以被解释为概率,常用于二分类问题的输出层,其中接近0的值表示一种类别,接近1的值表示另一种类别。此外,Sigmoid函数的平滑性和连续性使它在神经网络的早期非常受欢迎。
2.1.2 Sigmoid函数的导数和梯度消失
Sigmoid函数的导数可以通过链式法则计算得出:
f'(x) = f(x)(1 - f(x))
导数的这种形式在( f(x) )接近0或1时变得非常小,这会导致梯度消失的问题。梯度消失意味着在反向传播过程中,随着梯度向网络层的更深处传播,梯度值会指数级减少,这会减慢或阻止神经网络的训练,因为权重更新变得微不足道。
2.2 Sigmoid函数的实践应用
2.2.1 在逻辑回归中的应用
Sigmoid函数在逻辑回归中扮演着核心角色。逻辑回归是一种广泛用于二分类问题的算法。通过将线性回归的输出通过Sigmoid函数,我们可以得到一个介于0和1之间的概率值。这个概率值可以用来预测输入数据属于某个类别的可能性。
Sigmoid函数的输出可以被解释为概率,并使用交叉熵损失函数进行训练。这种组合使得逻辑回归成为许多分类任务的一个很好的起点。
2.2.2 在深度学习中的应用和局限性
在深度学习早期,Sigmoid函数因其数学特性和在逻辑回归中的成功应用而被广泛采用。然而,随着时间的推移,研究者们发现了Sigmoid函数的局限性,特别是梯度消失的问题。
在深层网络中,当反向传播更新权重时,梯度值会随每一层的传播而减少。这意味着较深层的神经元几乎没有学习的机会。为了解决这个问题,研究者们开始探索其他类型的激活函数,如ReLU,它在实践中表现出更好的性能,特别是在深层网络中。
代码块解释
以Sigmoid函数的Python实现为例:
import numpy as npdef sigmoid(x):return 1 / (1 + np.exp(-x))# 使用Sigmoid函数input_data = np.array([1, 2, 3])output_data = sigmoid(input_data)print(output_data)
在上述代码中,`sigmoid`函数使用了NumPy库来处理数学运算。`input_data`是一个NumPy数组,包含了我们想要应用Sigmoid函数的输入值。通过调用`sigmoid`函数,我们可以得到压缩在0到1之间的`output_data`。
流程图展示
下面是一个简化的流程图,描述了Sigmoid函数的工作原理:
graph LRA[输入数据] --> B[Sigmoid函数]B --> C[输出概率]C --> D[逻辑回归]
该流程图展示了从输入数据到应用Sigmoid函数,再通过逻辑回归进行分类的简单过程。尽管Sigmoid函数在逻辑回归中表现良好,但在更复杂的深度学习任务中,它遇到了一些挑战。
# 3. tanh激活函数
3.1 tanh函数理论基础
3.1.1 tanh函数的数学特性
双曲正切激活函数(tanh)是一种常见的神经网络激活函数,它将输入信号压缩至-1到1的区间内。数学上,tanh函数可以表示为:
[ ext{tanh}(x) = frac{e^x - e^{-x}}{e^x + e^{-x}} ]
该函数是一个关于原点对称的S形函数,输出均值接近零,比Sigmoid函数有更佳的中心化性质。tanh函数的输出范围在-1和1之间,当输入值为零时,输出为零。
在数学导数方面,tanh函数的导数可以通过以下公式计算:
[ ext{tanh}'(x) = 1 - ext{tanh}^2(x) ]
导数表示函数在某点的斜率,tanh的导数显示了激活函数在输入变化时的反应速度。当输入信号x接近无穷大或无穷小,tanh的导数趋近于零,这就是所谓的梯度消失现象。
3.1.2 tanh与Sigmoid的比较
tanh和Sigmoid激活函
到此这篇sigmoid函数与tanh(sigmoid函数与对率回归的联系)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/haskellbc/20944.html
