sigmoid输出是概率吗（sigmoid函数输出）



一、Logistic Regression 算法

Logistic Regression 算法具有复杂度低、容易实现的优点，我们可以利用 Logistic Regression 算法实现广告的点击率估计。Logistic Regression 模型是线性的分类的模型，所谓线性通俗的来说只需要一条直线就可以将不同的类区分开来。这条直线也成为超平面，使用

表示，其中W为权重，b为偏置。

在 Logistic Regression 算法中对样本进行分类，可以通过对训练样本的学习得到超平面，是数据分为正负两个类别。也可以使用阈值函数如 Sigmoid，将样本映射到不同的类别中。

二、Sigmoid 函数

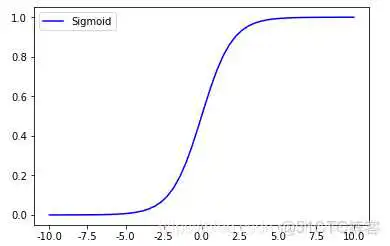
Sigmoid 函数的形式：

Sigmoid 函数的基本性质：

1. 定义域：(−∞,+∞)
2. 值域：(−1,1)
3. 函数在定义域内为连续和光滑函数
4. 处处可导，导数为：f′(x)=f(x)(1−f(x))

Python 实现 Sigmoid 函数如下：

三、那为什么使用 Sigmoid ? 有如下两种解释

（一）Logistic Regression 算法的需求

Logistic Regression 算法中属于正例即输入向量 X 的概率为 ：

P(y=1|x,w,b)=Sigmoid(Wx+b)

负例的概率为 ：

P(y=0|x,w,b)=1-P(y=1|x,w,b)

对于一个有效的分类器，Wx+b ( w 和 x 的内积）代表了数据 x 属于正类（y=1）的置信度。Wx+b 越大，这个数据属于正类的可能性越大, Wx+b 越小，属于反类的可能性越大。而 Sigmoid 函数恰好能够将 Wx+b 映射到条件概率P(y=1|x,w,b) 上。Sigmoid 函数的值域是（0,1），满足概率的要求，同时它是一个单调上升函数。最终， P(y=1|x,w,b)=Sigmoid(Wx+b)，sigmoid的这些良好性质恰好能满足 Logistic Regression 的需求。

（二）Sigmoid 函数和正态分布函数的积分形式形状非常类似。但计算正态分布的积分函数，计算代价非常大，而Sigmoid由于其公式简单，计算量非常的小。总之是 Sigmoid 函数能满足分类任务，至于其他的也不要纠结，很多人都在用就不要苦恼了。

四、求参数W和b

我们一般使用均方误差来衡量损失函数，但考虑均方误差损失函数一般是非凸函数，其在使用梯度下降算法的时候，容易得到局部最优解，不是全局最优解, 如下图所示：

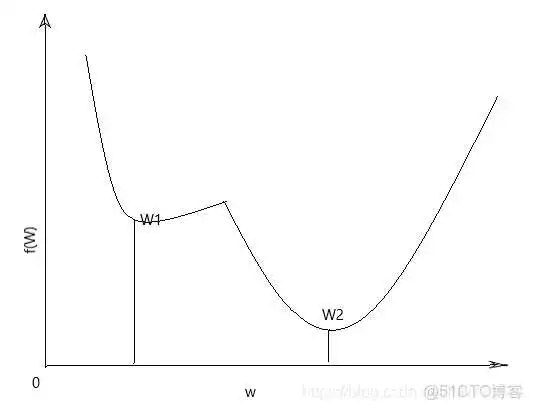
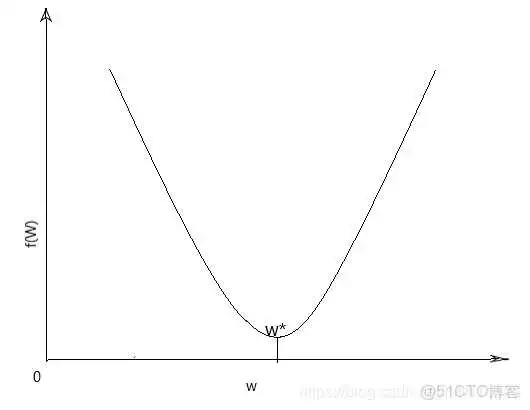
   非凸函数    凸函数

所以要选择凸函数，再者使用均方误差其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失，所以 Logistic Regression 算法选择交叉熵损失函数。

定义如下：

所以我们的问题变成：

五、梯度下降法

理清之后我们使用梯度下降的优化算法对损失函数 l 进行优化，寻找最优的参数 W。梯度下降法是一种迭代型的算法，根据初始点在每一次迭代的工程中选择下降方向，同时改变需要修改的参数。

梯度下降法的过程如下：

1. 随机选择一个初始点
2. 重复下面的步骤：

• 决定梯度下降的方向：
• 选择步长a
• 更新：

   3. 直到满足终止条件

梯度下降法的更新公式：

公式推导如下图：

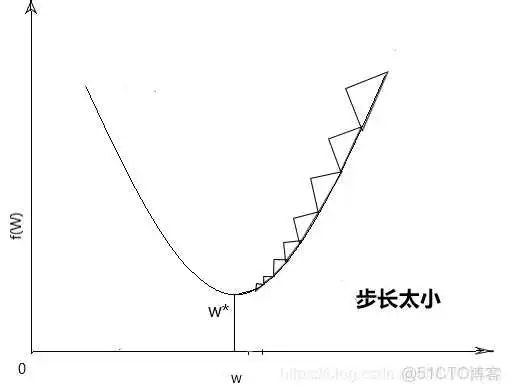
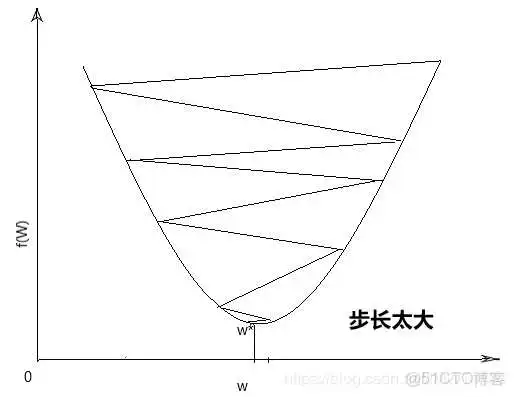
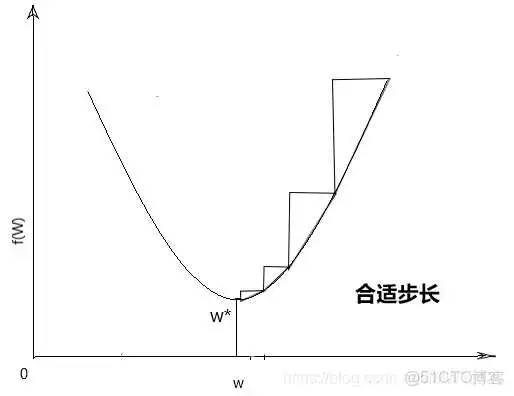
其中a为步长，选择太小会导致收敛速度很慢，选择太大会直接跳过最优解，如下图所示，所以步长的选择至关重要，负的梯度方向为下降方向。

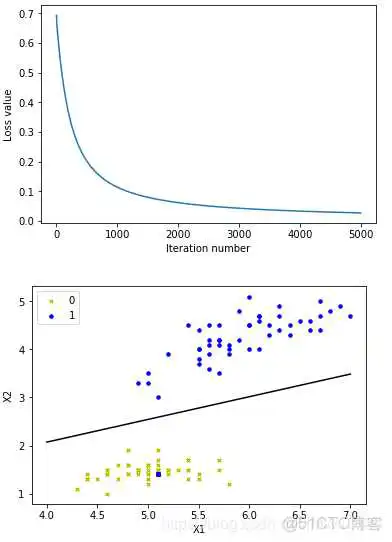
六、 Logistic Regression 算法应用

参考文献：

赵志勇《Python 机器学习算法》

Coursera机器学习课程

版权声明：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/20876.html