广度优先搜索和深度优先搜索都属于什么算法（广度优先搜索和深度优先搜索的使用场合）



算法是作用于具体数据结构之上的，深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。这是因为，图这种数据结构的表达能力很强，大部分涉及搜索的场景都可以抽象成“图”。

图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。为了搞清楚图的搜索算法，必须先把图的存储方式理解透彻。

图有多种存储方法，最常用的两种分别是：邻接矩阵和出边数组。

邻接矩阵的存储方式如下图所示，底层依赖一个二维数组。

对于无向图来说，如果顶点i与顶点j之间有边，我们就将A[i][j]和 A[j][i]标记1；对于有向图来说，如果顶点i到顶点j之间，有一条箭头从顶点i指向顶点j的边，那我们就将A[i][j]标记为1。同理，如果有一条箭头从顶点j指向顶点i的边，我们就将A[j][i]标记为1。对于带权图，数组中就存储相应的权重。

用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间。对于无向图来说，如果A[i][j]等于1，那A[j][i]也肯定等于1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。

针对上面邻接矩阵比较浪费内存空间的问题，出边数组可以避免空间浪费。如下图所示，每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。

例如上图中，我们要确定，是否存在一条从顶点2到顶点4的边，那我们就要遍历顶点2的所有出边，看出边是否能到达顶点4。所以，比起邻接矩阵的存储方式，在出边数组中查询两个顶点之间的关系就没那么高效了。

深度优先搜索用的是一种比较著名的算法思想，回溯思想。这种思想解决问题的过程，非常适合用递归来实现。例如下图中演示了用深度优先搜索的思想寻找一条从点s到点c的路径的方法。从图中我们可以看出，深度优先搜索找出来的路径，并不是点s到点c的最短路径。

我把上面的过程用递归的形式写下来如下。深度优先搜索代码里，有个比较特殊的全局变量found，它的作用是，当我们已经找到终止点之后，我们就不再递归地继续查找了。

理解了深度优先搜索算法之后，深度优先搜索的时间、空间复杂度是多少呢？从示意图可以看出，每条边最多会被访问两次，一次是遍历，一次是回退。所以，图上的深度优先搜索算法的时间复杂度是O(E)，E表示边数。深度优先搜索算法的消耗内存主要是visited、数组和递归调用栈。visited数组的大小跟顶点的个数V成正比，递归调用栈的最大深度不会超过顶点的个数，所以总的空间复杂度就是O(V)。

广度优先搜索直观地讲，就是一种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜索。理解起来并不难，示意图如下。

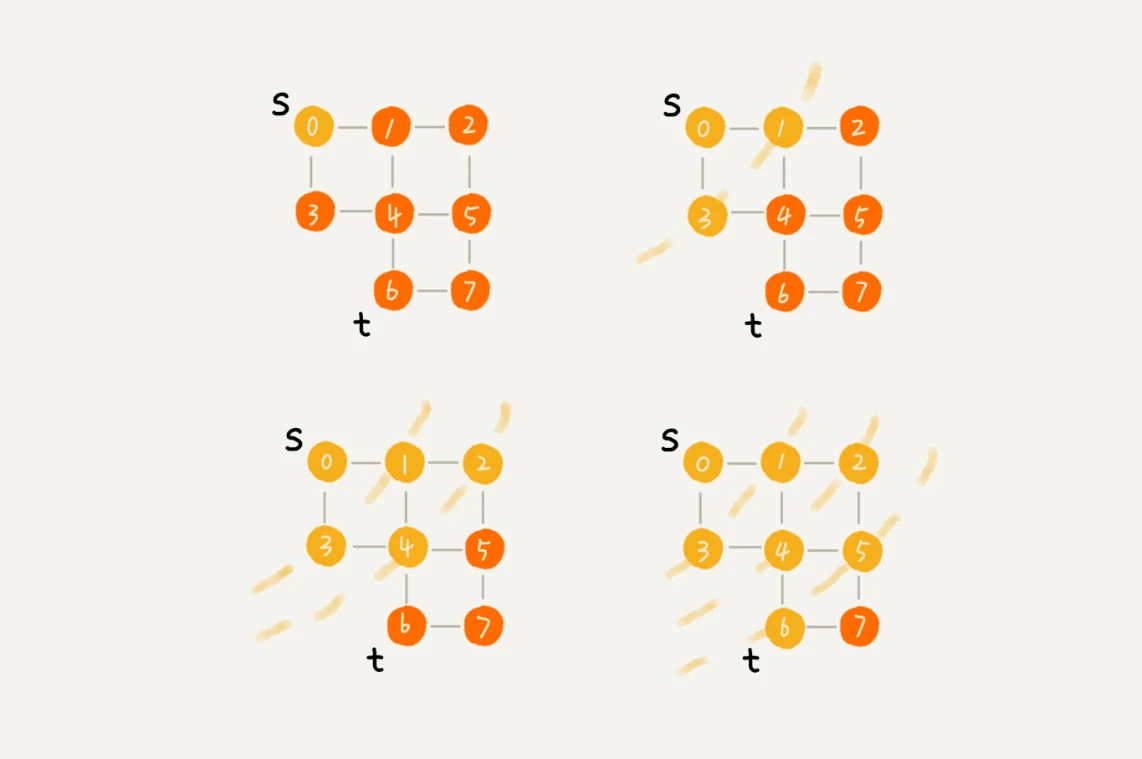
尽管广度优先搜索的原理挺简单，但代码实现还是稍微有点复杂度。实际上，这样得到的一条路径就是从起始点到指定点的最短路径。

BFS代码中的queue是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的，也就是说，我们只有把第k层的顶点都访问完成之后，才能访问第k+1层的顶点。当我们访问到第k层的顶点的时候，我们需要把第k层的顶点记录下来，稍后才能通过第k层的顶点来找第k+1层的顶点。所以，我们用这个队列来实现记录的功能。

广度优先搜索的时间、空间复杂度是多少呢？最坏情况下，终止顶点t离起始顶点s很远，需要遍历完整个图才能找到。这个时候，每个顶点都要进出一遍队列，每个边也都会被访问一次，所以，广度优先搜索的时间复杂度是 O(V+E)，其中，V表示顶点的个数，E表示边的个数。当然，对于一个连通图来说，也就是说一个图中的所有顶点都是连通的，E肯定要大于等于V-1，所以，广度优先搜索的时间复杂度也可以简写为O(E)。空间消耗主要在几个辅助变量visited数组、queue队列上。这三个存储空间的大小都不会超过顶点的个数，所以空间复杂度是O(V)。

样题一：岛屿的数量

给你一个由’1’(陆地)和 ‘0’(水)组成的的二维网格，请你计算网格中岛屿的数量。岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围。

DFS的思路：将二维网格看成一个无向图，竖直或水平相邻的点’1’之间有边相连。为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为’1’，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的’1’都会被重新标记。

最终岛屿的数量就是我们进行深度优先搜索的次数。

同样地，我们也可以使用广度优先搜索代替深度优先搜索。

BFS的思路：为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为‘1’，则将其加入队列，开始进行广度优先搜索。在广度优先搜索的过程中，从原点出发能到达的每个点‘1’都会被重新标记。直到队列为空，搜索结束。

最终岛屿的数量就是我们进行广度优先搜索的次数。

样题二：被包围的区域

注意关键解释：被围绕的区域不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

问题可以转化为：从边界上的‘O’出发所有能被访问到的‘O’都不能被填充为’X’，剩下的‘O’可以被填充为’X’，这是一个搜索问题。

思路：将所有存在于边界上的点’O’都打上标记，例如标记为’#‘，然后从这些点出发作搜索，所有能到达的点’O’也打上标记’#‘，最后将矩阵中所有标记为’#‘的点都填充为’O’，所有为’O’的点都填充为’X’。

DFS思路下的代码。

BFS思路下的代码。

样题三：省份数量

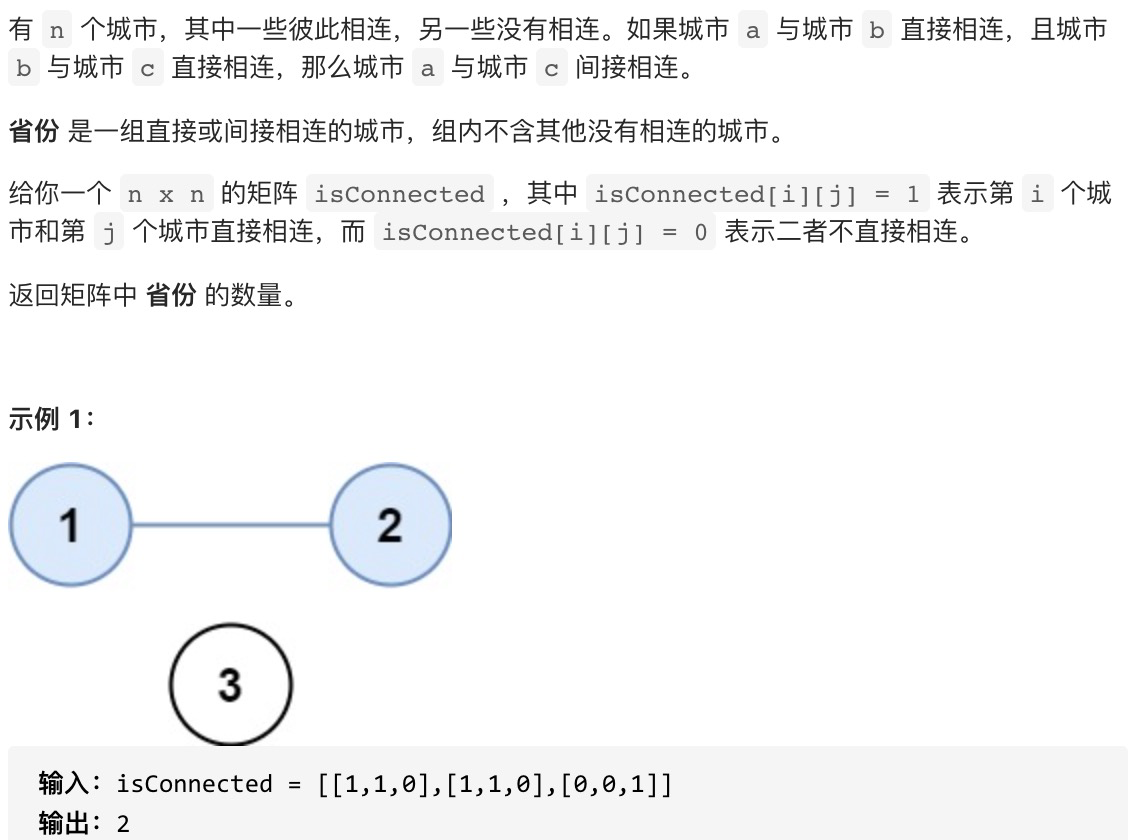
思路：给出的矩阵isConnected其实就是典型的邻接矩阵，这种图的存储方式很简洁。对于无向图，矩阵按对角线对称。问题可以转化成求无向图中连通块的个数，顶点数量为n，顶点的编号为0到n-1，矩阵isConnected描述了各个顶点的连接情况（矩阵中有一半信息是冗余的）。只需要从一个顶点出发遍历其能到达的其他所有顶点，当前顶点与其能到达的其他顶点构成连通块，统计这样的连通块的个数。

DFS与BFS的思路都能解决此问题，代码如下：

样题四：马走日

马在中国象棋以日字形规则移动，给定一个大小为n*m的棋盘，并指定一个初始坐标（x，y），要求不能重复经过棋盘上的同一个点，计算马可以有多少种途径可以遍历棋盘上的所有点，输出一个整数，表示马能遍历棋盘所有点的途径总数，若无法遍历所有点则输出0。输入的测试数据为一行四个整数，分别表示棋盘的大小以及初始位置坐标n、m、x、y。

样例输入：

样例输出：

思路：使用深搜去搜索，每走到一个点就做上标记，在一条路走到底的时候，取消已遍历节点的标记，标记的节点数大于棋盘上的总节点数则为一种遍历方法，停止遍历，累计遍历方法即可。

样题五：马走日-最小步数

马在中国象棋以日字形规则移动，给定一个大小为n*m的棋盘，并指定一个初始位置（x，y）和目标坐标（targetX,targetY），求出马从最初位置到目标位置所走的最少步数，若无法走到目标位置返回-1。

样例输入，棋盘是8X8，初始位置为(0,0)，目标位置为(2,0)

样例输出，最小步数为2

思路：采用BFS的方法。1、把起点放入到队列中；2、队列非空，取下一次可以跳到的位置，如果这个位置此前没有被访问，这表示可以进行访问，因为存在回溯的情况，把位置加入到队列中；3、如果此时可以调的位置等于目标位置，则输出最短步长。BFS遍历一遍棋盘，时间复杂度 O(n*m)。

广度优先搜索，通俗的理解就是，地毯式层层推进，从起始顶点开始，依次往外遍历，遍历得到的路径就是，起始顶点到终止顶点的最短路径。广度优先搜索需要借助队列来实现。深度优先搜索用的是回溯思想，非常适合用递归实现。二者是图上的两种最常用、最基本的搜索算法，比起其他高级的搜索算法，比如A*、IDA*等，要简单粗暴，没有什么优化，所以，也被叫作暴力搜索算法。所以，这两种搜索算法仅适用于状态空间不大，也就是说图不大的搜索。

版权声明：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/rgzn-sdxx/54831.html