Mounted at /content/drive
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度可能不高
适用数据类型:数值型和标称型数据
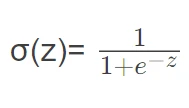
这是一个使用梯度上升算法进行逻辑回归的函数。主要步骤如下:
- 导入numpy库,用于矩阵运算。
- 定义函数gradAscent,接受输入参数dataMatIn和classLabels。
- 将dataMatIn和classLabels转化为矩阵,并进行转置,得到dataMatrix和labelMat。
- 获取dataMatrix的行数m和列数n。
- 设置学习率alpha为0.001,并设定最大迭代次数maxCycles为500。
- 初始化权重weights为全1的n行1列矩阵。
- 进行maxCycles次迭代:
a. 计算当前权重对应的预测结果h,通过sigmoid函数将dataMatrix与weights相乘得到。
b. 计算误差error,即真实标签labelMat与预测结果h的差。
c. 更新权重weights,通过乘以学习率alpha,再乘以dataMatrix的转置,再乘以误差error。
- 返回最终的权重weights。
总结:该函数通过梯度上升算法求解逻辑回归模型的权重参数,其中使用了sigmoid函数作为激活函数,并通过迭代优化权重参数,使得模型的预测结果与真实标签尽可能接近。最终返回的权重参数可以用于预测新的数据样本的类别。
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
plotBestFit(weights.getA())
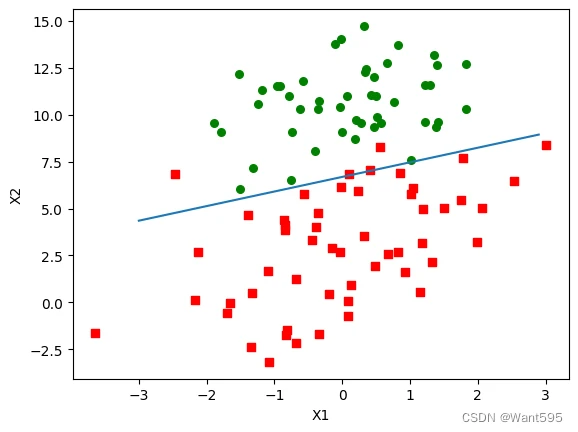
这段代码实现了逻辑回归的随机梯度上升算法。逻辑回归是一种二分类的机器学习算法,用于预测二分类问题的结果。该算法通过最大化似然函数来更新权重,从而使得模型的预测结果与实际结果最接近。
算法的输入包括数据集的特征矩阵(dataMatrix)、数据集的标签(classLabels)和迭代次数(numIter),默认为150次。其中,特征矩阵是一个m行n列的矩阵,m表示样本的数量,n表示特征的数量;标签是一个长度为m的向量,表示每个样本的分类标签。
算法的输出是更新后的权重(weights),这些权重用于预测新样本的分类结果。
算法的主要步骤如下:
- 初始化权重为一个长度为n的向量,每个元素的初始值为1。
- 对于给定的迭代次数,重复以下步骤:
a. 初始化一个包含样本索引的列表(dataIndex)。
b. 对于每个样本,重复以下步骤:
i. 计算学习率(alpha),其中alpha的值随着迭代次数和样本的索引i和j的变化而变化。这里使用的是固定的学习率,并加上一个小的常数以避免除零错误。
ii. 从dataIndex中随机选择一个样本的索引(randIndex)。
iii. 计算样本的预测概率(h)。这里使用的是sigmoid函数将线性组合转换为[0, 1]之间的概率值。
iv. 计算误差(error),即实际标签(classLabels)与预测概率(h)之间的差值。
v. 更新权重(weights)。根据梯度上升算法,使用学习率(alpha)乘以误差(error)乘以样本的特征值(dataMatrix[randIndex]),然后将得到的结果加到权重(weights)上。
vi. 从dataIndex中删除已经使用过的样本索引(randIndex)。
- 返回更新后的权重。
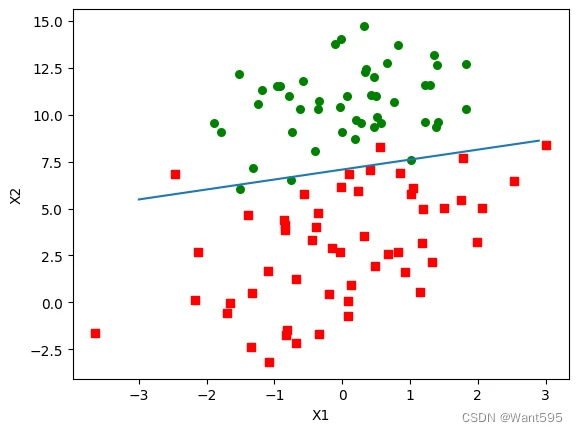
该算法每次迭代都使用一个随机的样本来更新权重,因此被称为随机梯度上升算法。相比于批量梯度上升算法,随机梯度上升算法的计算效率更高,但收敛速度较慢,并且对于噪声数据更敏感。
到此这篇关于Python Logistic算法使用详解的文章就介绍到这了,更多相关Python Logistic算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
到此这篇sigmoid算法(sigmoid函数实现)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/haskellbc/58013.html
