教学研讨所选素材大多来自国家教育资源公共服务平台、人教网等权威媒体，由网友推荐，阳光备课整合，仅供各位老师学习和研究，各部分版权归原作者所有。
▍来源：网络
一、教材分析
教材截图
（考虑到部分教师未有2019版课本，这里对教材截个图）
教材分析：
一、内容与内容解析
1.内容
n次方根的定义及其性质，分数指数幂的定义，有理数指数幂的定义与运算性质．
2.内容解析
教科书章引言一方面指出了章头图所蕴含的数学模型，另一方面还列举了这些数学模型的其他背景实例，从而指出本章将类比幂函数的研究方法，学习指数函数、对数函数的概念、图象和性质，并对这几类基本初等函数的变化差异进行比较，以及运用它们解决一些实际问题．
教科书章头图是良渚遗址．通过章引言，指出生物体死亡后，体内碳14的含量随着时间的变化按一定的规律衰减，引出本章将要学习的指数函数．在实际应用中，往往是先通过技术手段测出死亡生物体内碳14的含量，然后根据指数函数建立生物体内碳14的含量与死亡时间的关系，并利用对数和对数函数推算生物死亡的大致时间，从而实现考古的目的．由于死亡生物体内碳14的含量随时间连续变化，说明引进分数指数幂和无理数指数幂的必要性，并为指数函数的定义域是实数集提供了现实背景．
研究函数必先掌握运算，而数及其运算是推动数学发展的源泉和动力之一，是数学的基石．指数幂运算和对数运算是两类基本运算，对数运算与指数幂运算紧密相连，需要转化成指数幂运算，因此，熟练掌握指数幂运算是本章的基础．
指数幂运算的本质是数的自乘，把整数指数幂运算推广到有理数指数幂运算的本质就是使用新的运算符号表示根式运算和分式运算（负数指数幂运算），简而言之就是从一个符号的规定再到另一个符号的规定.只要能够准确进行两种运算符号的转化即可.而有理数指数幂这种数学运算符号表示的简洁性、运算的便捷性都优于分式和根式，这一符号的产生具有其必然性.比如：a与b的算术平均数为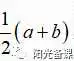
，几何平均数为
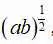，可理解为运算级的上升.事实上从16世纪比利时数学家斯蒂文尝试用分数对应根式开始，历经17世纪牛顿用有理数指数幂符号表示根式，直至18世纪欧拉才明确给出定义，这一表示法才被人们普遍接受和使用.指数幂运算的发展史充分说明基于数学语言的简洁性、准确性和合理性，有理数指数幂运算符号的产生与完善是有其历史必然性的.
教科书在研究幂函数时把正方形场地的边长c关于面积S的函数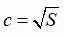
记作
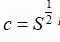引出分数指数幂的表示法.数学中，引进一个新的概念或法则时，总希望它与已有的概念或法则相容，于是从根式的意义入手，将正整数指数幂转化为被开方数的指数能被根指数整除的根式，推广到被开方数的指数不能被根指数整除的根式，又为了希望整数指数幂的运算能与其相容，于是只规定了被开方数为正数的分数指数运算.事实上分数指数幂是根式的一种新的表示方法，其表示的简洁性、运算的便捷性都优于根式．而负数为被开方数的分数指数幂是需要扩充到复数空间研究的，不能用根式解释，故此时讨论
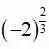之类的问题也是没有意义的.
因此本节课的教学重点是：根式与有理数指数幂的意义及运算性质.
二、目标与目标解析
1.教学目标
（1）经历n次方根定义形成过程，理解根式的意义，掌握根式的性质．
（2）了解分数指数幂表示的合理性、简洁性，掌握根式与分数指数幂间的互化.
（3）理解有理数指数幂意义，掌握其运算性质，并通过初步应用提升数学运算核心素养.
达成如上目标的标志是：
（1）学生能从平方根、立方根的概念学习过程中，归纳出一个数的n次方根定义，并能结合具体的例子理解n次方根的含义，及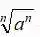
在n为奇数和偶数时化简的结果，特别是n为偶数时的情况.
（2）学生通过将正整数指数幂转化为被开方数的指数能被根指数整除的根式，推广到被开方数的指数不能被根指数整除的根式，再进一步分析这一运算法则规定的合理性，通过根式与分数指数幂的互化，理解分数指数幂的意义．
（3）学生能正确地完成根式及有理数指数幂的化简运算.
三、问题诊断分析
虽然学生已经掌握了整数指数幂的概念及其运算性质，并在学习幂函数的过程中接触过二次根式的分数指数幂的符号表示，但是由于n次方根及有理指数幂比较抽象，学生理解起来还是有困难．
因此本节课教学难点是：理解根式及分数指数幂的定义，及有理数指数幂的运算性质.
教科书是通过复习平方根、立方根的定义，然后类比出n次方根，归纳类比出n次方根的一般定义与性质. n次方根的性质实际上是平方根、立方根性质的推广．教学时，可以用平方根、立方根、四次方根为基础来加以说明，加深对这一性质的理解.分数指数是指数概念的又一次推广，教学中应多举实例让学生理解分数指数幂的意义，明确分数指数幂是根式的一种新的写法，并通过根式和分数指数幂的互化区分负数指数幂与分数指数幂的不同，巩固、加深对有理数指数幂的理解.
更多：http://www.pep.com.cn/gzsx/xrjbgzsx/xrjgzwd/201911/t20191128_1947596.html
四、教学重点、难点
重点是：根式与有理数指数幂的意义及运算性质.
难点是：理解根式及分数指数幂的定义，及有理数指数幂的运算性质.
五、数学学科素养
1.数学抽象：n次方根、根式的概念与分数指数幂的概念；
2.逻辑推理：分数指数幂和根式之间的互化；
3.数学运算：利用分数指数幂的运算性质化简求值；
4.数学建模：通过与初中所学的知识进行类比，得出分数指数幂的概念，和指数幂的性质。
六、教学过程：见《研讨素材二》
相关：
1.突破难点 | “4.1.1 n次方根与分数指数幂”教学设计（新旧各2个）
2.教案精选 | 4.1.1 n次方根与分数指数幂（2019版新教材）
3.课件精选 | 4.1.1根式与分数指数幂·课件Ⅱ（2019版新教材）
4.2.1.1指数与指数幂的运算(分数指数幂等)的教学
5.教学研讨｜4.1指数（第2课时）4.1.2 无理数指数幂及其运算性质（2019版新教材）
6.教案精选 | 4.1.2 无理数指数幂及其运算性质（2019版新教材）
| 2.1.1 指数与指数幂的运算 |
| 2.1.2指数函数及其性质 |
| 提前备课|指数函数 （第一课时）的教学 |
根据文末留言的要求，考虑到初三上高一学生预习的需要，这里提供教材的练习、习题及复习参考题等等习题答案，可能有错漏，仅供各位学生朋友参考。
相关：
教学研讨｜ 1.1集合的概念 （2019版新教材）
教学研讨｜1.2集合间的基本关系（2019版新教材）
教学研讨｜1.3.1集合的基本运算第1课时 并集、交集（2019版新教材）
教学研讨｜1.4 充分条件与必要条件（2019版新教材）
教学研讨｜1.5.1 全称量词与存在量词（2019版新教材）
教学研讨｜2.1 等式性质与不等式性质（2019版新教材）
教学研讨｜ 2.2 基本不等式（2课时）（2019版新教材）
教学研讨｜2.3 二次函数与一元二次方程、不等式 第1课时（2019版新教材）
教学研讨｜2.3 二次函数与一元二次方程、不等式 第2课时（2019版新教材）
教学研讨｜3.1.1 函数的概念 第1课时（2019版新教材）
教学研讨｜3.1.1 函数的概念 第2课时（2019版新教材）
教学研讨｜3.1.2 函数的表示法第1课时（2019版新教材）
教学研讨｜3.1.2 函数的表示法 第2课时（2019版新教材）
教学研讨｜3.2.1 函数的单调性与最大（小）值（2019版新教材）
教学研讨｜3.2.2 函数的奇偶性（2019版新教材）
教学研讨｜3.3 幂函数教学设计（2019版新教材）
END
全
文
完
-----全文到此为止。整理不易，如果喜欢，请点下“在看”和转发到朋友圈。
特别推荐(点下列标题进入)：
A.数学教师必备 | 手机版《高中数学教学手册》，请收藏！
14.【学生课本·教师用书】13个学科67家出版社直接下载；
15.人教版教科书、教师用书电子版来啦！快快下载；
免责声明
【内容由网上搜索而来，由阳光备课整合，各部分版权归原作者所有，在此向作者致谢！摘录、转载，是想为经济欠发达地区教师提高业务水平做点事,仅此而已,如有侵权,请联系删除,谢谢!】
点击↓阅读原文↓更多！
版权声明：
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！
转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/55415.html