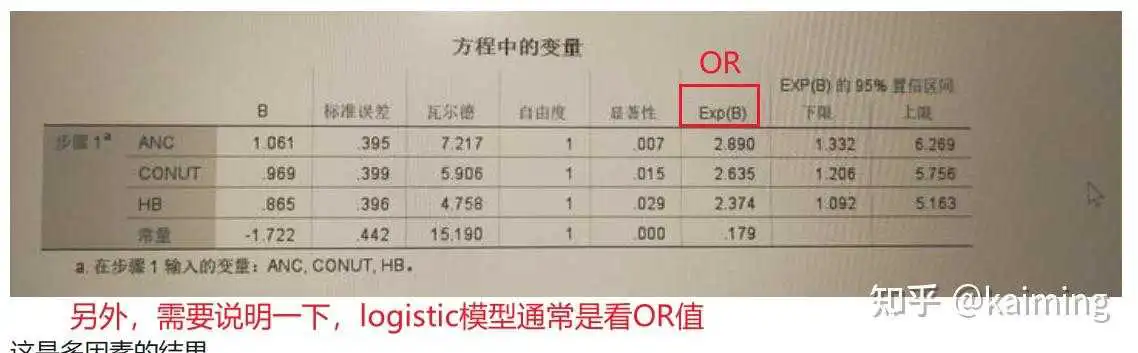
sigmoid函数和logistic（sigmoid和logistic的区别）

根据您提供的SPSS的结果，模型的公式应该是：

$logit(p)=1.061*ANC+0.969*CONUT+0.865*HB-1.722$

在何谓数据？数据可视化真的那么神奇吗？一文中，我们了解到数据的类型分为离散型和连续型两种，而在一般讨论的回归模型中，解释变量x和被解释变量y常常指的是连续型数据，那么当离散型数据出现，我们又该如何构建回归模型呢？

当解释变量为离散型数据时，我们可以将其转化为哑变量/虚拟变量来进行线性回归；而当被解释变量是离散型数据时，“上不封顶、下没底线”的线性拟合就满足不了离散型因变量的实际取值情况了，如何将离散型因变量和连续型自变量的关系连接起来变成了一个“世纪难题”。（这里模型的估计方法也发生了改变，先挖个坑，后续再讲讲花生了什么）

所幸，在19世纪三四十年代的人口数量增长研究中，数理统计学派创始人阿道夫· 凯特勒（Adolphe Quetelet）意识到地球的资源是有限的，地球上的人口数量不可能一直呈指数增长无限扩大。于是，阿道夫· 凯特勒让他的学生维尔赫斯特（Pierre François Verhulst）仔细研究这个课题。

维尔赫斯特尝试了许多不同的函数来拟合人口增长的阻力，最终发明了一种可以对1833年以前法国、比利时、俄罗斯等国家的人口数据进行“完美”拟和的函数——那就是logistic函数！但是，在此后将近一个世纪的时间里，Logistic函数在学术界几乎无人问津，反而是利用标准正态分布的累积分布函数作为两点分布概率函数的Probit模型大行其道。

直到1920年，美国食品管理局统计学部的主要负责人雷蒙德·佩尔（Raymond Pearl）和罗威尔·里德（Lowell Reed），在研究美国人口增长和粮食需求时，重新发现了这种S-型曲线可以很好地拟合1790~1910年的美国人口数据。

1929年，罗威尔·里德与他的学生约瑟夫·伯克森（Joseph Berkson）合作将Logistic曲线应用到化学领域的自催化反应过程。随后，约瑟夫·伯克森经过深入的统计研究，于1944年正式提出可以用Logistic函数来代替正态分布的累积函数，并模仿Bliss创造的“Probit”一词，将“the log of an odds”缩写为“Logit”，Logit模型的姓名由此诞生。

有意思的是，当Logit模型刚被提出的时候，很多学者并不接受，甚至有人认为Logit模型要比Probit模型“低人一等”。这主要是因为在当时，人们还无法将Logit模型中的随机项与某种特定的分布联系起来——Probit模型中的随机项服从正态分布，相比之下有着更深厚的统计理论基础。

一直到1974年，丹尼尔·麦克法登（Daniel L. McFadden）从随机效用理论出发，将Logit模型与Gumbel分布联系起来，从而奠定了Logit模型的理论基础——McFadden本人也因此项发现获得了2000年的诺贝尔经济学奖。值得一提的是，Gumbel分布作为极值分布的一种类型，应用价值非常之大，常用于极端情况的预测，如十年一遇的地震，百年一遇的洪水，千年一遇的风暴等发生概率极小，一旦发生损失极大的现象。

至此，Logit模型经过两个世纪的跨越，从刚开始出世时的无人问津，到后来几度与世人邂逅但擦肩而过，最终终于有人拿起放大镜仔细观察研究，为其筑建坚实的理论堡垒，才迎来了自己的春天，成为许多学者研究离散型数据和极端概率事件的一大利器。可见——真金不怕火炼，金子总会发光。

下一篇，我们再讲讲“Logit”中的“it”是什么，以及如何解锁Logit模型回归结果的解读方式。

参考资料：

DCM笔记——Logistic回归的起源（上）

DCM笔记——Logistic回归的起源（中）

DCM笔记——Logistic回归的起源（下）

对于回归模型系数的解读，学过回归的同学都知道，一般线性模型y=βx＋ε中回归系数β的经济意义——解释变量x每增加一个单位，被解释变量y随之平均变化β，即x影响y的边际效应。而对于Logit和Probit这种非线性模型来说，其回归系数并非直接表示x影响y的边际效应，从其累积分布函数的表现也可以看出，x影响y的边际效应也是不断变化的。

由于逻辑分布的累积分布函数有明确的解析表达式：P(y=1|x)=F(x,β)=exp(x'β)/[1-exp(x'β)]，而标准正态分布则没有，使得Logit模型的计算相比Probit模型更方便，同时也赋予了Logit模型的回归系数更容易通过数理知识进行解读的优势，故Logit模型逐渐成为离散选择模型的老大哥。

那么，我们应该如何对Logit模型的回归结果进行解读呢？今天我们就从三大法宝切入来回答这个问题。（还不赶紧拿小本本记下……不对，还不赶紧点赞收藏）

在Logit的来源 | 一场跨世纪的漂流之旅一文中，我们讲到“Logit”的名字起源于约瑟夫·伯克森将“the log of an odds”简化而来，“Logit”拆分开来就是“Log-it”，这里的“it”指的就是“odds”。

那么问题来了：啥是odds？

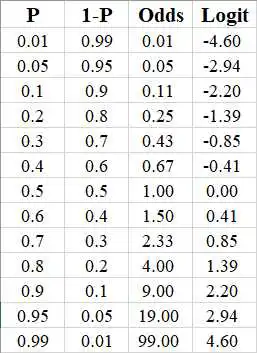
英文odds的涵义有（事件的）发生比、胜算、几率，我们通常用以指代某个事件发生的“几率”。这里，事件发生的几率odds与事件发生的概率Probability是有所不同的，具体我们看公式：

① 概率Probability

= 事件A发生的频数/所有结果出现的频数

= P(A)

② 几率Odds

= 事件A发生的概率/事件A未发生的概率

= P(A)/1-P(A)

以掷骰子为例，我们定义事件A为掷一次骰子得到的点数为6，那么该事件发生的概率为P=1/6，几率（胜算）为odds=(1/6) / (5/6)=1/5。几率odds的产生最初是为了赌博中的公平起见——在对赌时，由于点数不为6发生的概率是点数为6发生的概率的5倍，两种赌注面临的相对风险不一样，因此，赌点数不为6的赌注也应该是赌点数为6的赌注的5倍，这样才能保证赌博的公平。

再回过头来看，“Logit”就是“Log-it”，“it”就是“odds”，连起来——Logit=log(odds)。这里的log实际上是以e为底的自然对数ln，对于神秘又常见的e，想要深入了解的小伙伴，推荐阅读自然对数的底“e”到底是怎么来的？一文。

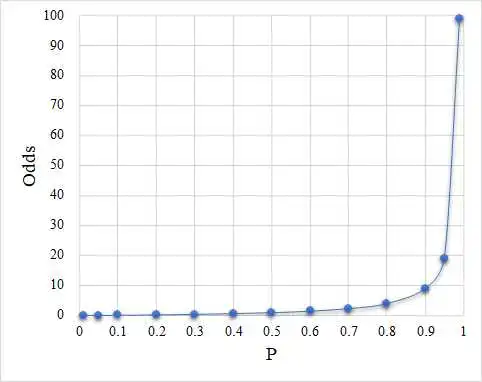
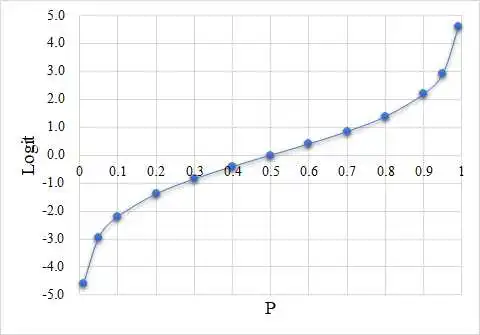
由此我们就有了Logit模型的基本函数形式：

从Logit模型的公式可以看出，等式左边为对数几率log-odds，等式右边为线性函数，回归系数β表示的是解释变量x每增加一单位，引起对数几率log-odds的边际变化。由于取对数意味着百分比的变化，故此时回归系数β的第一种解读方式可以是：在其他变量不变的情况下，x每增加一单位，引起y发生的几率odds的变化百分比。具体地，当β＞0，意味着x每增加一单位，y发生的几率将增加β×100%；当β＜0，意味着x每增加一单位，y发生的几率将降低β×100%。

如果你的解释变量x也是离散型变量（如性别、学历、年龄阶段等），还有另一种更直接的解读方法——几率比odds ratio。

几率比，顾名思义，即两个几率的比值，那是哪两个几率呢？举个栗子。

我们假设影响企业是否开展技术创新的其中一个解释变量x为企业所处的市场是否成熟（充分竞争），在其他变量条件不变的情况下，当x=0为不成熟市场时，企业开展技术创新的几率为p0/1-p0，当x=1为成熟市场时，企业开展技术创新的几率为p1/1-p1，倘若x增加1单位，也即企业所处的市场由不成熟市场转变为成熟市场，我们将这两种市场下企业开展技术创新的几率进行一场PK，此时数学运算的奥妙就发生了：

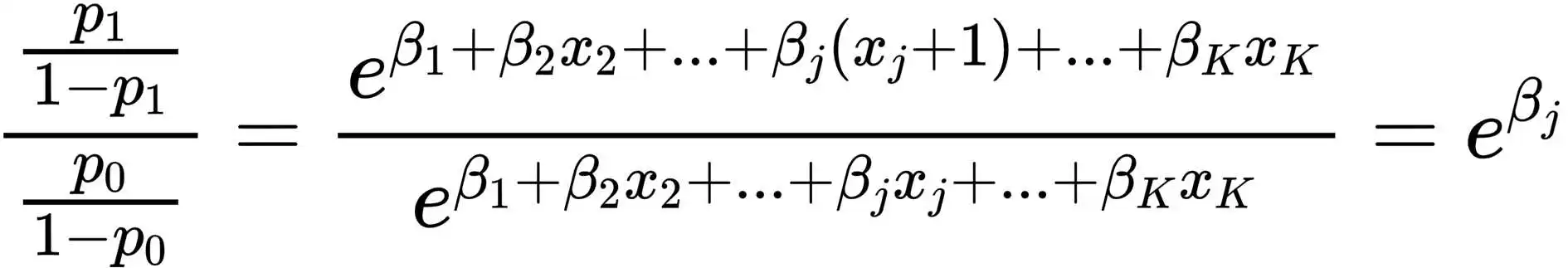
可以看到，成熟市场下企业开展技术创新的几率与不成熟市场下企业技术创新的几率的比值——几率比，恰好等于e^β。因此，我们就有了另一种解读方式：当其他变量保持不变时，分类变量x增加1单位，即x的取值从参照类(x=0)变化到目标类(x=1)时，目标类发生y的几率是参照类发生y的几率的e^β倍，或y发生的几率将变化|e^β-1|×100%。

在上例中，回归结果即可解读为：在其他条件不变的情况下，企业在成熟市场开展技术创新的几率是在不成熟市场的e^β倍。或者，若β大于0：当企业所处的市场由不成熟转为成熟时，企业开展技术创新的几率将增加(e^β-1)×100%；若β小于0：当企业所处的市场由不成熟转为成熟时，企业开展技术创新的几率将降低(1-e^β)×100%。

以上两种方法就是Logit模型胜于Probit模型的系数可解读性优势，除此之外，两个模型共通的解释方式就是通过边际效应来解读。

对于连续型自变量，边际效应的本质就是求偏导，根据链式法则：

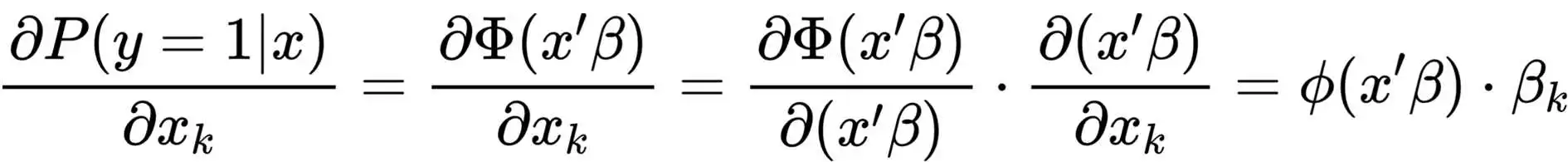
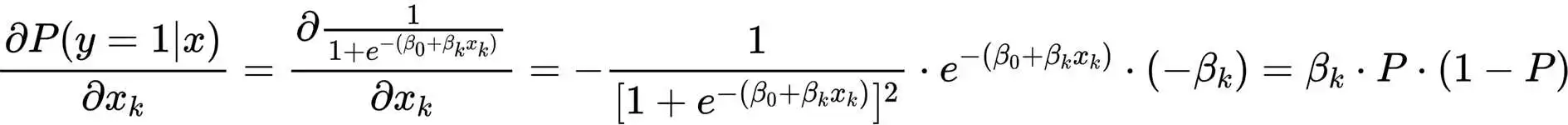
由偏导结果可以看出，Logit模型和Probit模型的边际效应都不是常数，且是随着解释变量x而变化的，因此，对于边际效应的估计也就和解释变量x的大小脱不了干系，常用的边际效应往往要从自变量x上做文章：

1-平均边际效应

2-在样本均值处x=mean(x)的边际效应

3-在某个代表值处x=x0的边际效应

当我们限定了x，就可以得到在该条件下确定的边际效应。软件可以直接帮我们运算输出边际效应的大小，此时的结果解读只需在一般的边际效应的基础上，强调是哪种边际效应：在其他变量保持不变的情况下，x每增加1单位，y发生的概率平均变化多少多少；或者，在样本均值处/某个代表值处，x每增加1单位，y发生的概率将变化多少多少。

对于离散型自变量，边际效应本质上则是目标类x=0和参考类x=1两者对应y发生概率的差，此时对0-1变量取均值或者单独取某个代表值没有任何意义，所以一般情况下是直接对每个样本观测值的边际效应进行简单的算术平均，用“平均边际效应”进行结果的解读。

下面主要使用Stata和R语言两款软件的官方案例数据，对二元Logit模型的实现和结果进行展示，感兴趣的同学可以运用上面的3种解读方式，对以下案例结果进行解读。

. webuse nhanes2d . sum highbp height weight age female //数据的基本特征 Variable | Obs Mean Std. dev. Min Max -------------+--------------------------------------------------------- highbp | 10,351 . . 0 1 height | 10,351 167.6509 9. 135.5 200 weight | 10,351 71.89752 15.35642 30.84 175.88 age | 10,351 47.57965 17.21483 20 74 female | 10,351 . . 0 1 . logit highbp height weight age female, r //构建二元Logit模型，r表示使用普通的稳健标准误 Iteration 0: log pseudolikelihood = -7050.7655 Iteration 1: log pseudolikelihood = -5853.749 Iteration 2: log pseudolikelihood = -5839.6214 Iteration 3: log pseudolikelihood = -5839.5795 Iteration 4: log pseudolikelihood = -5839.5795 Logistic regression Number of obs = 10,351 Wald chi2(4) = 1845.12 Prob > chi2 = 0.0000 Log pseudolikelihood = -5839.5795 Pseudo R2 = 0.1718 ------------------------------------------------------------------------------ | Robust highbp | Coefficient std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | -.0 .003729 -9.54 0.000 -.0 -.0 weight | .0 .001855 26.95 0.000 .0 .0 age | .0 .0014459 32.45 0.000 .0 .049757 female | -. .0 -5.86 0.000 -. -. _cons | -.074346 . -0.12 0.906 -1. 1. ------------------------------------------------------------------------------ . logit highbp height weight age female, r or //or表示显示几率比(odds ratio)，而不显示回归系数β Iteration 0: log pseudolikelihood = -7050.7655 Iteration 1: log pseudolikelihood = -5853.749 Iteration 2: log pseudolikelihood = -5839.6214 Iteration 3: log pseudolikelihood = -5839.5795 Iteration 4: log pseudolikelihood = -5839.5795 Logistic regression Number of obs = 10,351 Wald chi2(4) = 1845.12 Prob > chi2 = 0.0000 Log pseudolikelihood = -5839.5795 Pseudo R2 = 0.1718 ------------------------------------------------------------------------------ | Robust highbp | Odds ratio std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | . .0035987 -9.54 0.000 . . weight | 1.051268 .0019501 26.95 0.000 1.047452 1.055097 age | 1.048041 .0015153 32.45 0.000 1.045076 1.051016 female | . .0 -5.86 0.000 . . _cons | . . -0.12 0.906 . 3. ------------------------------------------------------------------------------ Note: _cons estimates baseline odds. . predict p //计算概率预测值p (option pr assumed; Pr(highbp)) . margins, dydx(*) //计算所有解释变量(*)的平均边际效应 Average marginal effects Number of obs = 10,351 Model VCE: Robust Expression: Pr(highbp), predict() dy/dx wrt: height weight age female ------------------------------------------------------------------------------ | Delta-method | dy/dx std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | -.0068101 .0007018 -9.70 0.000 -.0081855 -.0054347 weight | .009574 .0003091 30.98 0.000 .0089682 .0 age | .0089854 .0002253 39.88 0.000 .0085438 .0094271 female | -.0 .0 -5.88 0.000 -.0 -.0 ------------------------------------------------------------------------------ . margins, dydx(height) //计算解释变量height的平均边际效应 Average marginal effects Number of obs = 10,351 Model VCE: Robust Expression: Pr(highbp), predict() dy/dx wrt: height ------------------------------------------------------------------------------ | Delta-method | dy/dx std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | -.0068101 .0007018 -9.70 0.000 -.0081855 -.0054347 ------------------------------------------------------------------------------ . margins, dydx(*) atmeans //计算所有解释变量(*)在样本均值处的边际效应 Conditional marginal effects Number of obs = 10,351 Model VCE: Robust Expression: Pr(highbp), predict() dy/dx wrt: height weight age female At: height = 167.6509 (mean) weight = 71.89752 (mean) age = 47.57965 (mean) female = . (mean) ------------------------------------------------------------------------------ | Delta-method | dy/dx std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | -.0085336 .0008944 -9.54 0.000 -.0 -.0067806 weight | .0 .0004458 26.91 0.000 .0 .0 age | .0 .0003443 32.70 0.000 .0 .0 female | -.0 .0 -5.86 0.000 -. -.0 ------------------------------------------------------------------------------ . margins, dydx(*) at (age=35) //计算所有解释变量(*)在年龄为35岁处的平均边际效应 Average marginal effects Number of obs = 10,351 Model VCE: Robust Expression: Pr(highbp), predict() dy/dx wrt: height weight age female At: age = 35 ------------------------------------------------------------------------------ | Delta-method | dy/dx std. err. z P>|z| [95% conf. interval] -------------+---------------------------------------------------------------- height | -.0065589 .0006909 -9.49 0.000 -.007913 -.0052049 weight | .0092209 .0003122 29.54 0.000 .0086091 .0098327 age | .008654 .0002142 40.40 0.000 .0082342 .0090739 female | -.069207 .0 -5.82 0.000 -.0 -.0 ------------------------------------------------------------------------------

> # 调包 > library(knitr) > library(margins) Warning message: 程辑包‘margins’是用R版本4.2.2 来建造的 > # 导入数据 > infert <- data.frame(infert) > # 查看数据特征（数据集详细介绍：https://www.rdocumentation.org/packages/datasets/versions/3.6.2/topics/infert） > print(summary(infert)) education age parity induced case spontaneous stratum 0-5yrs : 12 Min. :21.00 Min. :1.000 Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. : 1.00 6-11yrs:120 1st Qu.:28.00 1st Qu.:1.000 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:21.00 12+ yrs:116 Median :31.00 Median :2.000 Median :0.0000 Median :0.0000 Median :0.0000 Median :42.00 Mean :31.50 Mean :2.093 Mean :0.5726 Mean :0.3347 Mean :0.5766 Mean :41.87 3rd Qu.:35.25 3rd Qu.:3.000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:62.25 Max. :44.00 Max. :6.000 Max. :2.0000 Max. :1.0000 Max. :2.0000 Max. :83.00 pooled.stratum Min. : 1.00 1st Qu.:19.00 Median :36.00 Mean :33.58 3rd Qu.:48.25 Max. :63.00 > # 构建Logit模型 > lg <- glm(case ~ age + parity + induced + spontaneous + stratum + pooled.stratum, family = binomial, data = infert) > # 输出回归系数结果 > summary(lg) Call: glm(formula = case ~ age + parity + induced + spontaneous + stratum + pooled.stratum, family = binomial, data = infert) Deviance Residuals: Min 1Q Median 3Q Max -1.8228 -0.7872 -0.4797 0.8690 2.6432 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.41394 1.13597 -2.125 0.033587 * age 0.04869 0.03052 1.595 0. parity -0.66191 0.19947 -3.318 0.000906 * induced 1.35386 0.30868 4.386 1.15e-05 * spontaneous 2.08742 0.31539 6.619 3.63e-11 * stratum 0.00822 0.01261 0.652 0. pooled.stratum -0.02814 0.01763 -1.596 0. --- Signif. codes: 0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 316.17 on 247 degrees of freedom Residual deviance: 256.76 on 241 degrees of freedom AIC: 270.76 Number of Fisher Scoring iterations: 4 > # 输出几率比OR值 > print(exp(lg$coefficients)) (Intercept) age parity induced spontaneous stratum pooled.stratum 0.0 1.0 0. 3. 8.0 1.00 0. > # 输出平均边际效应 > print(summary(margins(lg))) factor AME SE z p lower upper age 0.0084 0.0052 1.6239 0.1044 -0.0017 0.0185 induced 0.2330 0.0461 5.0578 0.0000 0.1427 0.3233 parity -0.1139 0.0317 -3.5896 0.0003 -0.1761 -0.0517 pooled.stratum -0.0048 0.0030 -1.6220 0.1048 -0.0107 0.0010 spontaneous 0.3593 0.0344 10.4557 0.0000 0.2919 0.4266 stratum 0.0014 0.0022 0.6535 0.5135 -0.0028 0.0057

最后，有个趣味思考——Logit模型和Logistic模型是一个模型吗？

闭着眼睛回忆一下Logistic模型，两者长得好像不一样？！

实际上，两者本质是同一模型，只不过函数表达方式不一样罢了。我们对Logit模型两边求e次方的指数运算，再通过移项得出的概率P的函数表达式，就是Logistic模型本尊：）

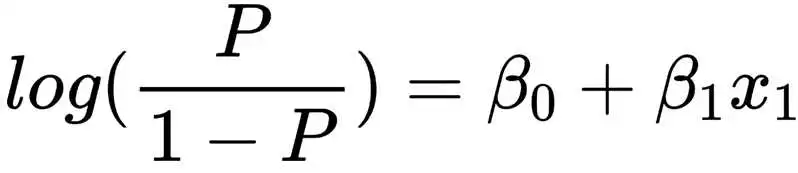
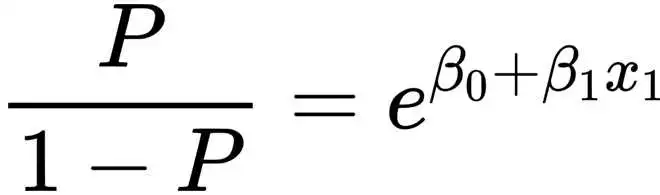
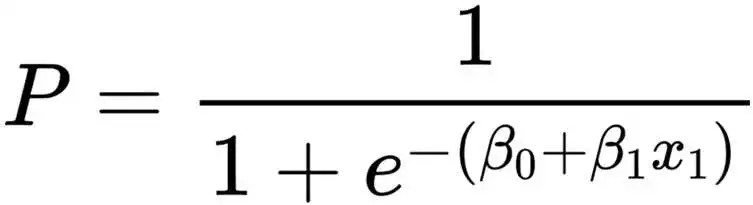
本篇主要讲<经典统计学中的Logistic模型回归结果解读和案例展示>，若对<机器学习中的Logistic模型建模和预测>感兴趣，欢迎点赞点关注，关注人数多的话我们再单独出一篇来讲解，那么感谢收看，我们下期再见：-）

PROC LOGISTIC的CLASS statement默认的option是PARM=EFFECT，这一点与PROC PHREG不同（default为PARM=REF）。

PARM=REF：各水平与第一个level进行比较。

PARM=EFFECT：将每个水平都看作独立的参数进行估计和解释，没有明确的基准水平；各水平与所有水平的平均效果进行比较。

解决方案：在CLASS中指定option为PARM=REF

Logistic函数（logistic function）^[1]一般指函数 $N(t)={e^Z\over1+e^Z}$ 其中 $Z=\alpha+\beta t$ （并没有一个专门的符号来表示这个函数）。

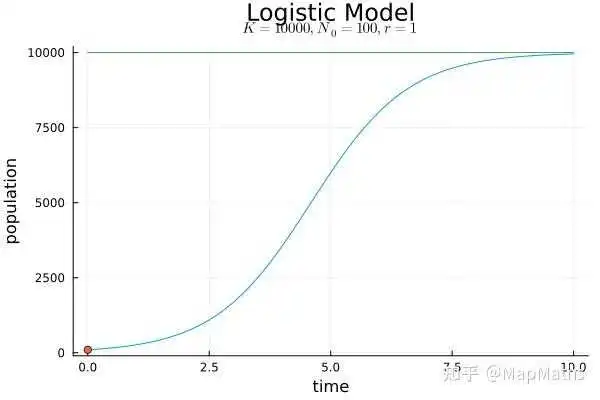
Logistic函数是Logistic微分方程的解，后者最初的目的是作为描述人口增长的模型（当然，描述物种繁衍也可以），更准确地说，是作为Malthus人口模型的修正。Logistic模型最早由比利时数学家Pierre-François Verhulst（1804-1849）于1838-1847年间引入，但后来又被重新发现过（Raymond PearI和Lowell J. Reed，1920），不过两次发现都是缘于人口问题，并得出了相同的结论。^[2]

简单地说，可以将Malthus模型看成经典的“J型曲线”而将Logistic函数的图像看作“S型曲线（sigmoid curve）”，因此Logistic函数属于数学中所谓的“S型函数（sigmoid function）”，事实上我们直接将它的图像称为Logistic曲线（logistic curve）毕竟数学中长得像S的函数的确太多了（例如 $\tanh$ ）。在生物课上学到的知识告诉我们Malthus描述的模型只可能局部地存在，而Logistic模型才是更接近真相的。

此后，Logistic函数又被广泛运用在了概率论、机器学习等领域；而由Logistic微分方程衍生出的Logistic差分方程中人们发现了神奇的混沌现象，并催化出了《周期三意味着混沌》这篇混沌理论的“开山之作”（李天岩，Yorke，1977）以及费根鲍姆常数；当然它在一些和人口模型类似的领域里也有直接应用，例如物理学和化学。不过由于本人才疏学浅，就只能在本文中涵盖一些关于“解逻辑斯蒂微分方程”之类浅显的知识点，也希望各位大佬能够提出一些意见建议。下面是正文。

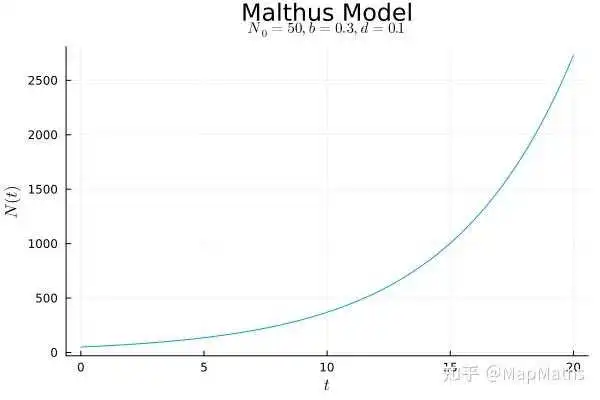
作为人口学的一个经典结论，Malthus在《人口原理》（1798）中提出了类似于下面这样的数学模型^[3]：

研究某地的人口变化，若不考虑移民等不可控因素，而仅考虑出生和死亡的情况：我们可暂且用 $N(t)$ 表示 $t$ 时刻该地的人口数量，用 $\beta(t)$ 和 $\delta(t)$ 分别表示 $t$ 时刻的出生率（即单位时间内的出生人数与总人口的比值）和死亡率（即单位时间内的死亡人数与总人口的比值），并将初始时刻 $t=0$ 时的人口记作 $N_0:=N(0)$ 作为初始条件。

若在很短的时间 $[t,t+\Delta t]$ 内研究，我们就可以列出一个差分方程来近似描述人口变化情况： $\Delta N=\beta(t)N(t)\Delta t-\delta(t)N(t)\Delta t=[\beta(t)-\delta(t)]N(t)\Delta t\tag1$

将其转化为微分方程，得到： ${\mathrm dN(t)\over\mathrm dt}=[\beta(t)-\delta(t)]N(t)\tag2$

Malthus理论的关键在于他假设出生率和死亡率都为常数： $\beta(t)\equiv b$ 、 $\delta(t)\equiv d$ ，

于是： ${\mathrm dN(t)\over\mathrm dt}=(b-d)N(t)\tag3$ 容易解得： $N(t)=N_0e^{(b-d)t}\tag4$ 若 $b>d$ （人口持续增长），这就是一个J型曲线：

在 $t$ 趋于无穷时，N会不断增大到无穷大，这是不合理的——至少在一个自然生态系统中我们从来没有观察到这种情况。

生物学的知识也告诉我们某地的物种繁衍在经过很长时间后应该会趋于某一个定值，而不是无穷大——也就是S型曲线。

那么，Malthus的理论究竟错在哪儿呢？

Verhulst认为，问题在于出生率和死亡率不应该是定值。

事实上，如果我们在一开始将人口的净增长率设为 $\rho(t):=\beta(t)-\delta(t)$ ，那么根据Malthus的假设， $\rho(t)$ 将是一个定值，这已经不符合我们的常识了。我们知道，当人口很大（暂且忽略某些不可控的人为因素）时，该地的资源会不够所有这些人使用，也许还会有疾病发生。总而言之，此时死亡率可能会升高，而出生率将降低，因此净增长率应该也会降低，并不断趋近于 $0$ ，最终人口数也应该趋近于一个定值，我们将其记作 $K$ ，称之为环境容纳量。

经过试验，Verhulst认为净增长率应该是总人口的一个单调递减的一次函数，例如： $\rho(t)={r(K-N)\over K}\tag5$

其中 $r$ 是一个正的常数。

将其代入 $(2)$ ，我们就得到了Logistic微分方程（logistic differential equation）： ${\mathrm dN(t)\over\mathrm dt}={rN(K-N)\over K}\tag6$

（你可能会看到这个方程的不同版本，但实际上它们是等价的）

别忘了初始条件： $N(0)=N_0\tag7$

通常而言，我们只考虑： $0<N_0<K\tag8$

可以看到，Logistic微分方程是非线性的，但幸运的是，它很容易解。

下面的任务就是解这个方程：

为了打字方便（打 $\LaTeX$ 真的很累），下面我将 $N(t)$ 直接记为 $N$ ，但请记住它是 $t$ 的函数；同时我也会用蓝色的 $\color{blue}{C_n}$ 来表示解方程过程中的常数。

首先，将 $(6)$ 变为： ${\mathrm dN\over N(K-N)}={r\mathrm dt\over K}\tag9$ 两边积分：

$\int{\mathrm dN\over N(K-N)}=\frac{rt}K\tag{10}$ 左边这个积分的关键在于一个裂项： $\begin{aligned}\int{\mathrm dN\over N(K-N)}&= \int\frac1K\left(\frac1N+\frac1{K-N}\right)\mathrm dN\\&=\frac{\int{\mathrm dN\over N}+\int{\mathrm dN\over K-N}}K\\&=\frac{\ln|N|+\ln|K-N|}K\\&=\frac{\ln\left(\left|\frac N{K-N}\right|\right)}K\end{aligned}\tag{11}$ 代回 $(10)$ ，这就得到： $\ln\left(\left|\frac N{K-N}\right|\right)=rt+\color{blue}{C_1}\tag{12}$ 化为指数式： $\frac N{K-N}=\pm\color{blue}{C_2}e^{rt}\tag{13}$

由于 $N$ 可导必连续且 $K\neq N$ ，因而 $K-N$ 的符号总是不变，可化为：

$\frac N{K-N}=\color{blue}{C_3}e^{rt}\tag{14}$

于是： $N=K\color{blue}{C_3}e^{rt}-N\color{blue}{C_3}e^{rt}\tag{15}$ $N\left(\color{blue}{C_3}e^{rt}+1\right)=K\color{blue}{C_3}e^{rt}\tag{16}$ 最终得到： $N={K\color{blue}{C_3}e^{rt}\over\color{blue}{C_3}e^{rt}+1}=\frac K{1+\color{blue}{C_4}e^{-rt}}\tag{17}$ 代入初始条件，解得： $\color{blue}{C_4}=\frac{K-N_0}{N_0}\tag{18}$

最终得到Logistic函数： $N(t)={\frac{K-N_0}{N_0}Ke^{rt}\over\frac{K-N_0}{N_0}e^{rt}+1}=\frac K{1+\frac{K-N_0}{N_0}e^{-rt}}\tag{19}$ 将其稍微化一化就能变成开头提到的形式了。

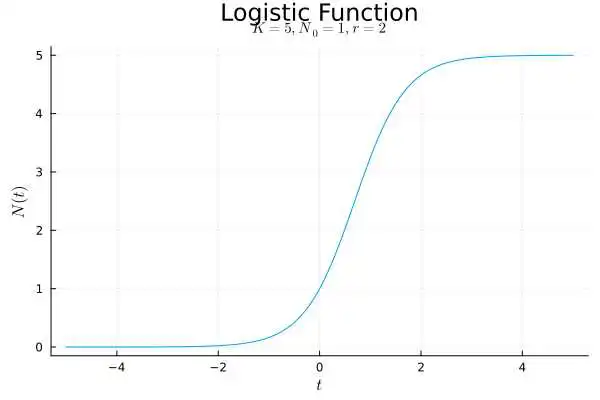
这里简单讨论（水）一下这个函数的性质：

首先， $t=0$ 时 $N(t)=N_0\enspace(0<N_0<K)$ ，这是初始条件。

接着， $t\rightarrow-\infty$ 时 $e^{-rt}\rightarrow\infty$ ，因此 $N(t)\rightarrow0$ ；

而当 $t\rightarrow+\infty$ 时 $e^{-rt}\rightarrow0$ ，因此 $N(t)\rightarrow K$ 。

容易证明，该函数在 $0<N_0<K$ 时严格增且有上下界。

正如我在开头提到的，双曲正切函数 $\tanh$ 也是一个S型函数。事实上，它的图像与Logistic曲线长得如此相像以致于我们可以找到合适的参数使得……

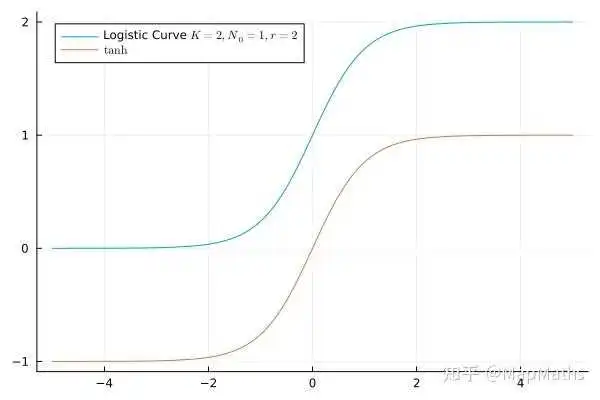
……你能一眼看出这两个函数其实可以互相平移得到（在某些参数下，平移之后还要进行缩放）。

从我们已经得到的Logistic函数的解析式中，你当然可以推出这个结论，但其实Logistic微分方程还有另一种简单的解法，并且这个解法能够直接得到Logistic函数与 $\tanh$ 的关系。

我们再回到Logistic微分方程的这个变形：

$\int{\mathrm dN\over N(K-N)}=\frac{rt}K\tag{10}$

只不过这次我们将用配方法解决左边这个积分：

$\begin{aligned}\int{\mathrm dN\over N(K-N)}&= -\int\frac{\mathrm dN}{N^2-KN}\\&=-\int{\mathrm dN\over\left(N-\frac K2\right)^2-\frac{K^2}4}\\&=-\int{\mathrm dN\over\frac{K^2}4\left[\left(\frac2KN-1\right)^2-1\right]}\\&=\frac4{K^2}\int{\mathrm dN\over1-\left(\frac2KN-1\right)^2}\end{aligned}\tag{20}$

接着，因为 $\left(\tanh^{-1}x\right)'=\frac1{1-x^2}\enspace(|x|<1)$ ，且有 $0<N<K$ ，于是：

$\int{\mathrm dN\over N(K-N)}=\frac4{K^2}\cdot\frac K2\tanh^{-1}\left(\frac2KN-1\right)=\frac2K\tanh^{-1}\left(\frac2KN-1\right)\tag{21}$

代回 $(10)$ ，得： $\tanh^{-1}\left(\frac2KN-1\right)=\frac{rt}2+\color{blue}{C_3}\tag{22}$

化为：

$N=\frac K2\left[\tanh\left(\frac{rt}2+\color{blue}{C_3}\right)+1\right]\tag{23}$

代入初始条件，解得：

$\color{blue}{C_3}=\tanh^{-1}\left(\frac{2N_0}K-1\right)\tag{24}$

就得到另一个形式的Logistic函数：

$N(t)=\frac K2\left\{\tanh\left[\frac{rt}2+\tanh^{-1}\left(\frac{2N_0}K-1\right)\right]+1\right\}\tag{25}$

这样，Logistic函数就不再神秘了：它就是函数 $\tanh$ 经过一个简单的放缩和平移之后得到的结果。

容易验证 $K=2,\space N_0=1,\space r=2$ 时确实有 $N(t)-1=\tanh(t)$

前面我们只考虑了 $0<N_0<K$ 的情况，然而 $N_0>K$ 时确实也有现实意义。然而这时的Logistic曲线就不再是一个S型曲线了。

事实上，在推导式 $(19)$ 的过程中我并没有用到 $0<N_0<K$ 这个条件，因此式 $(19)$ 是永远成立的。而推导式 $(25)$ 的时候我确实用到了这个条件，然而在 $N_0>K$ 时，由于 $\left(\coth^{-1}x\right)'=\frac1{1-x^2}\enspace(|x|>1)$ ，所以只需要把所有的 $\tanh$ 都用 $\coth$ 替换掉即可。

以Malthus模型作为引入，我们得出了Logistic（微分）方程： ${\mathrm dN(t)\over\mathrm dt}={rN(K-N)\over K}$

以及它的解——Logistic函数——的表达式： $N(t)={\frac{K-N_0}{N_0}Ke^{rt}\over\frac{K-N_0}{N_0}e^{rt}+1}=\frac K{1+\frac{K-N_0}{N_0}e^{-rt}}$

并得出了该函数与双曲正切函数的关系： $N(t)=\frac K2\left\{\tanh\left[\frac{rt}2+\tanh^{-1}\left(\frac{2N_0}K-1\right)\right]+1\right\}$

说明：持续更新GPT在线大模型和开源大模型相关技术！！！！
更多详细的技术文档，在这里学习和免费领取哈。学习视频：木羽Cheney的B站视频

全文共13000余字，预计阅读时间约30~60分钟 | 满满干货，建议收藏！

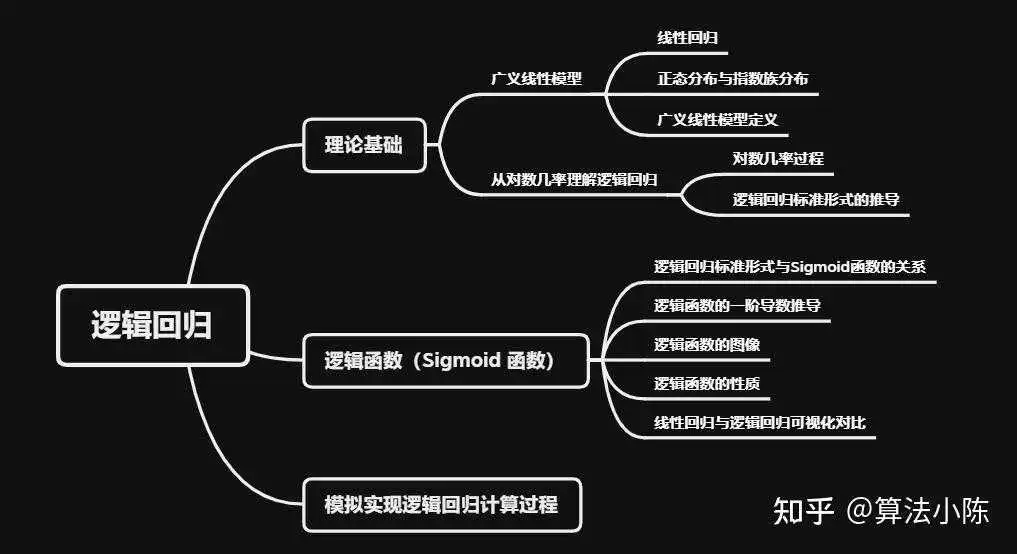
逻辑回归（Logistic Regression）是一种常用的分类方法，在机器学习和统计学中被广泛使用。尽管名字中包含“回归”，但实际上它是一种分类方法，主要用于二分类问题，同时也推广到了解决多分类问题。它通过拟合一个逻辑函数（或称为Sigmoid函数），将自变量和因变量之间的线性关系转换为概率。

逻辑回归模型的输出是一个概率值，通常，我们会设定一个阈值，当模型输出的概率大于这个阈值时，我们将样本判定为正类，否则判定为负类。

逻辑回归是一种统计建模方法，是广义线性模型（Generalized Linear Models，GLM）的一种特殊形式，它使用对数几率函数（logit function）作为链接函数，将特征和目标变量之间的关系建模为概率。该模型不仅能够处理二分类问题，还能很好地处理多分类问题。

在求解逻辑回归模型参数时，一般采用极大似然估计（Maximum Likelihood Estimate）方法，这个方法通过最大化似然函数(也就是观测到的数据的概率)来估计模型参数。除了极大似然估计，也可以使用KL散度来求解模型参数，这两种方法都是在寻找最佳的模型参数，使得模型对训练数据的预测尽可能接近实际观察到的结果，我们在后面会分别介绍这两种方法。

逻辑回归的这一建模思路不仅使模型在统计上具有较好的解释性，同时也让模型具有良好的预测能力，使其在许多实际应用中都得到了广泛的使用。

我们先从线性回归开始回顾。如果你还不了解线性回归，建议先看一下这篇文章：

算法小陈：机器学习(二)：线性回归的理论基础与最小二乘法实践

线性回归是最基本的预测模型之一。它假设目标变量（或响应变量）和输入特征（或预测变量）之间存在线性关系：

$y = w_0 + w_1x_1 + w_2x_2 + ... + w_nx_n + b \\$

或者等价的向量表示：

$y = w^T \cdot x + b \\$

这里， $w_1, w_2, ..., w_n$ 是模型参数， $b$ 是偏置项。

对于向量表示来说， $w^T$ 表示权重向量的转置， $x$ 是特征向量。 $w^T·x$ 表示的是权重向量和特征向量的点积，其结果就是每个特征和对应权重的乘积之和，和第一种写法一样。这种写法更为简洁，尤其在特征数量很多的情况下。

线性回归的目标是找到最佳的 w 和 b，使得预测的 y 尽可能接近真实的 y。

然而，线性回归的一个主要限制是它假设目标变量和输入特征之间的关系是线性的。

这里的“线性”，是相对于模型参数 w 而言的，即使y和x的关系在数学形式上为非线性（例如多项式，指数，对数等），只要这种关系可以写成参数w的线性组合形式，我们仍然可以使用线性回归模型。但是，当w和x之间的关系是非线性的，我们就需要更灵活的模型来处理这种情况。

此外，线性回归假设模型的误差项服从正态分布，而在现实中，目标变量可能不遵循这个假设，或者目标变量可能不是连续的（例如分类问题）。为了处理这些情况，就需要引入更为广泛的模型框架 —— 广义线性模型（GLM）。

广义线性模型不仅可以处理目标变量和输入特征之间非线性的关系，还可以处理目标变量不符合正态分布的情况。

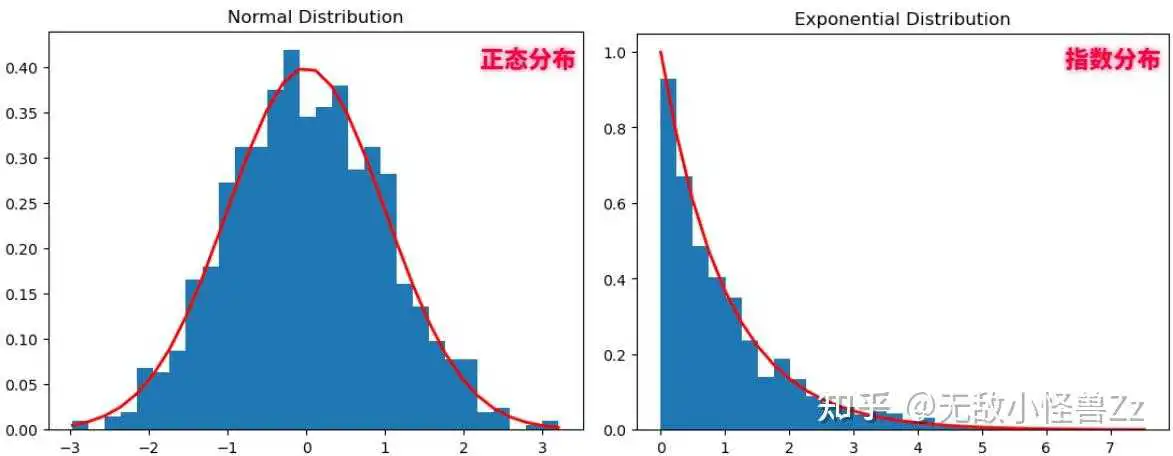
正态分布：也称为高斯分布，是一种在数学、物理和工程等领域都非常重要的概率分布。正态分布的概率密度函数是一个钟形曲线，其形状由两个参数决定，即平均值（或期望）μ和方差σ²。在正态分布的曲线下，观测值接近平均值的概率最高。

指数族分布：指数族分布是一大类概率分布，它包括许多常见的分布，如正态分布、二项分布、泊松分布、伽马分布等。这些分布被称为指数族，是因为它们的概率密度函数（或概率质量函数，对于离散分布）可以写成一个特定形式的指数函数。指数族分布在统计学中有许多重要的性质，使得它们在建模和推断中非常有用。

我们先使用numpy和matplotlib库来生成和展示这两种分布的曲线：

import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # 正态分布 mu, sigma = 0, 1 # mean and standard deviation s = np.random.normal(mu, sigma, 1000) count, bins, ignored = plt.hist(s, 30, density=True) plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)2 / (2 * sigma2) ), linewidth=2, color='r') plt.title('Normal Distribution') plt.show() # 指数分布 lam = 1.0 # rate lambda s = np.random.exponential(lam, 1000) count, bins, ignored = plt.hist(s, 30, density=True) plt.plot(bins, lam*np.exp(-lam*bins), linewidth=2, color='r') plt.title('Exponential Distribution') plt.show()

这个代码首先生成正态分布和指数分布的随机样本，然后创建了一个直方图，并在直方图上方绘制了相应的理论密度函数。红线是理论的概率密度函数。

在经典的线性回归模型中，我们假设误差项（也就是实际观测值与由模型预测的值之间的差）遵循正态分布。这个假设有助于我们进行参数估计（如最小二乘法），并进行各种统计检验和构建置信区间。正态分布假设使得线性回归模型的解析解可以容易地通过闭式公式得到，且在某些情况下，这个解是最优的。

逻辑回归是广义线性模型（GLM）的一种，GLM的框架允许我们对目标变量的分布做出更一般的假设。在逻辑回归中，我们假设响应变量遵循二项分布（这是指数族分布的一种），并且我们使用了对数几率链接函数，这使得我们可以在[0, 1]区间内建模概率。这种方式使得逻辑回归可以用于分类任务。

广义线性模型（GLM）是线性回归的一种扩展，它扩展了常规线性回归模型，以处理目标变量不符合正态分布的情况，提供了更多的灵活性。

GLM的核心思想是，允许目标变量服从指数族分布，而不仅仅是正态分布，同时通过一个链接函数将响应变量和预测变量连接起来，而不是直接的线性关系。

在GLM中，我们有：

$g(y) = w_1x_1 + w_2x_2 + ... + w_nx_n + b \\$

等价于向量形式：

$g(y) = w^T \cdot x + b \\$

这里， $g()$ 是链接函数， $w_1, w_2, ..., w_n$ 是模型参数， $b$ 是偏置项。

通过选择不同的分布和链接函数，GLM可以表示很多不同的统计模型。例如，当我们选择二项分布和对数几率链接函数时，我们就得到了逻辑回归模型；当我们选择泊松分布和对数链接函数时，我们就得到了泊松回归模型。这就引出了我们的主题：逻辑回归。

逻辑回归的基本原理和推导过程我们先从对数几率（log-odds）或 logit 函数的角度来理解，这也是 "Logistic Regression" 名称的来源。那我们就需要先了解下面的这些过程。

对于二分类问题，如果某个事件发生的概率为 $p$ ，那么该事件不发生的概率为 $1-p$ 。该事件的几率定义为发生概率与不发生概率的比值，即

$odds(p) = \frac{p}{(1-p)} \\$

取这个几率的对数，我们得到的就是对数几率（log-odds），也就是logit函数。对数几率的范围是全实数域，从负无穷到正无穷，这是其主要优点。

当我们选择二项分布和对数几率链接函数时，我们就得到了逻辑回归，写为以下的对数几率形式：

对数几率（log-odds）中的"log"通常指的是自然对数（即以e为底的对数，也就是"ln"）。在数学和统计学中，当我们只说"log"时，通常默认是指自然对数。所以，在许多文献和教材中，对数几率函数通常被写作ln(p/(1-p))。

$\ln \left(\frac{p}{1-p}\right) = w^T \cdot x + b \\$

即我们的线性预测器等于样本的对数几率。对上面的等式进行变换，我们可以解出$p$，也就是样本属于正类的概率： $p = \frac{e^{w^T \cdot x + b}}{1+e^{w^T \cdot x + b}} \\$

这就是逻辑回归的模型形式，它预测的是样本属于正类的概率。我们可以看到，虽然最初建立的是线性预测器，但是经过逻辑函数的映射，我们得到的预测值是在0到1之间的概率，通过对数几率，逻辑回归模型能够将线性回归模型的结果转化为一个预测类别的概率，这使得逻辑回归在处理分类问题上非常实用。

首先，我们从对数几率公式开始：

$\ln \left(\frac{p}{1-p}\right) = w^T \cdot x + b \\$

我们设 $w^T \cdot x + b = x$ ，于是我们有：

$\ln \left(\frac{p}{1-p}\right) = x \\$

然后对等式两边同时用 $e$ 指数化，我们有：

$\frac{p}{1-p} = e^x \\$

我们可以变形得到：

$p = e^x(1-p) \\$

然后我们将等式左边的所有 $p$ 提取出来：

$p (1 + e^x) = e^x \\$

最后，我们解出 $p$ ：

$p = \frac{e^x}{1 + e^x} \\$

最后，我们把 $x$ 替换回 $w^T \cdot x + b$ ，即得：

$p = \frac{1}{1 + e^{-(w^T \cdot x + b)}} \\$ 即： $y = \frac{1}{1 + e^{-(w^T \cdot x + b)}} \\$

这个等式就是逻辑回归的标准形式，其中 $y$ 表示样本属于正类的概率。

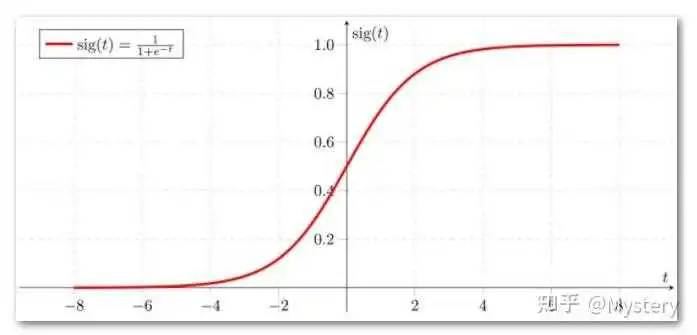
逻辑回归的标准形式实际上是sigmoid函数的一个特定形式。sigmoid函数是一种在生物学、人工神经网络和机器学习中广泛使用的S形函数，其公式为：

$f(x) = \frac{1}{1+e^{-x}} \\$

在逻辑回归中，我们将线性预测器 $w^T \cdot x + b$ 的结果通过sigmoid函数进行转换，得到的输出是一个介于0和1之间的概率值。这个值可以被解释为样本属于正类的概率。

所以，逻辑回归的标准形式实际上就是将线性预测器的结果输入到sigmoid函数中，并输出一个概率值。这就是逻辑回归与sigmoid函数的关系。

我们首先知道，sigmoid函数的定义为： $f(x) = \frac{1}{1+e^{-x}} \\$

我们对其进行微分，首先考虑到它的形式可以写为：

$f(x) = (1+e^{-x})^{-1} \\$

这样就变成了一个更标准的链式法则的形式。接下来我们将这个函数看作是两个函数的复合，即

$g(x) = 1+e^{-x} \\$

$f(g) = g^{-1} \\$

根据链式法则，我们有

$f'(x) = f'(g(x)) \cdot g'(x) \\$

对于上面的两个函数，它们的导数分别为

$g'(x) = -e^{-x} \\$

$f'(g) = -g^{-2} = - (1+e^{-x})^{-2} \\$

所以，按照链式法则，我们可以得到：

$f'(x) = f'(g(x)) \cdot g'(x) = - (1+e^{-x})^{-2} \cdot -e^{-x} = \frac{e^{-x}}{(1+e^{-x})^{2}} \\$

接下来，我们将其化简，为了化简，我们首先将上下都乘以 $e^{x}$ ，这样得到

$f'(x) = \frac{1}{(e^{x}+1)^{2}} \\$

然后，我们将其进一步简化，我们知道：

$f(x) = \frac{e^{x}}{e^{x}+1} \\$

这意味着，我们可以将上面的公式的分子替换为 $f(x)$，于是得到：

$f'(x) = f(x) \cdot \frac{1}{e^{x} + 1} \\$

然后我们注意到 $\frac{1}{e^{x} + 1} 就是 1 - f(x)$ ，于是，我们就得到：

$f'(x) = f(x) \cdot (1 - f(x)) \\$

这就是sigmoid函数的一阶导数。

我们生成一些数据并使用Matplotlib库绘制Sigmoid函数及其导数的图像。然后，我将解释该图像的主要特性。

import numpy as np import pandas as pd import matplotlib.pyplot as plt # 定义sigmoid函数和其一阶导数 def sigmoid(x): return 1 / (1 + np.exp(x)) def sigmoid_derivative(x): return sigmoid(x) * (1 - sigmoid(x)) # 生成数据 x = np.linspace(-10, 10, 100) y_sigmoid = sigmoid(x) y_derivative = sigmoid_derivative(x) # 生成数据框 data = pd.DataFrame({ 'x': x, 'sigmoid': y_sigmoid, 'derivative': y_derivative }) # 绘制sigmoid函数和其导数的图像 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.plot(data['x'], data['sigmoid'], label='sigmoid') plt.title('Sigmoid function') plt.xlabel('x') plt.ylabel('sigmoid(x)') plt.grid(True) plt.subplot(1, 2, 2) plt.plot(data['x'], data['derivative'], label='derivative', color='red') plt.title('Derivative of the sigmoid function') plt.xlabel('x') plt.ylabel('sigmoid\'(x)') plt.grid(True) plt.tight_layout() plt.show()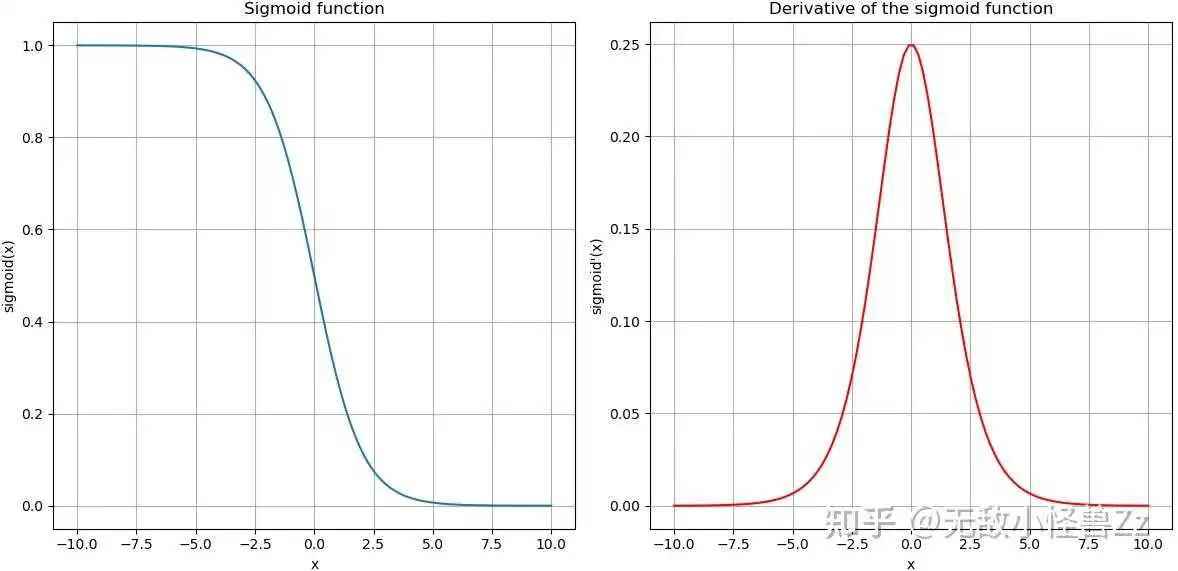

从图中，我们可以观察到以下特性：

Sigmoid函数：这个函数能够将输入的任何实值映射到(0, 1)区间内。这一性质使得sigmoid函数在分类问题中非常有用，因为我们可以将其输出解释为属于某个类别的概率。
Sigmoid函数的导数：这个函数在z=0处取得最大值0.25，而当z远离0时，导数值逐渐趋近于0。这说明，当输入值远离0时，sigmoid函数变化越来越慢。这就是所谓的“梯度饱和”问题
导数与原函数的关系：我们可以看到，sigmoid函数的导数可以表示为原函数的形式：sigmoid'(x) = sigmoid(x) * (1 - sigmoid(x))。这一性质在计算梯度时非常有用，因为我们已经计算出了sigmoid(x)，所以可以直接复用，而不需要再计算一次exp(-x)。

根据上一节的描述，我们可以得到逻辑函数的一些重要性质：

取值范围：逻辑函数的输出始终在0到1之间。这使得逻辑函数的输出可以被解释为概率，非常适合于处理分类问题。
单调性：逻辑函数是单调递增的。也就是说，x 的值越大，f(x) 的值越大；x 的值越小，f(x) 的值越小。
形状：逻辑函数的形状类似于 "S"。在 x 的值非常大或非常小的时候，f(x) 的值分别趋近于1和0。在 x=0 的时候，f(x)=0.5。
导数：逻辑函数的导数可以用函数自身表示，即：f'(x) = f(x) * (1 - f(x))。这个性质使得逻辑回归的参数更新（如梯度下降法）在计算上非常便利。

这些性质使得逻辑函数非常适合于逻辑回归模型。在逻辑回归模型中，我们假设特征和对数几率（log-odds）之间存在线性关系，然后通过逻辑函数将对数几率转换回概率。这样，我们就可以得到一个输出范围在0到1之间，可以被解释为概率的预测模型，非常适合于处理分类问题。

我们创建一些模拟数据并使用线性回归和逻辑回归对其进行拟合。

import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression, LogisticRegression # 创建模拟数据 np.random.seed(0) n = 100 # 数据点数量 x = np.linspace(0, 10, n) y = np.where(x + np.random.normal(0, 1, n) > 5, 1, 0) # 添加一些噪声 # 转换为 DataFrame data = pd.DataFrame({'x': x, 'y': y}) # 线性回归 lr = LinearRegression() lr.fit(data[['x']], data['y']) # 逻辑回归 logr = LogisticRegression(solver='lbfgs') logr.fit(data[['x']], data['y']) # 创建图表 plt.figure(figsize=(10, 6)) # 绘制原始数据 plt.scatter(data['x'], data['y'], alpha=0.5, label='Data') # 绘制线性回归的预测结果 plt.plot(data['x'], lr.predict(data[['x']]), label='Linear Regression') # 绘制逻辑回归的预测结果 plt.plot(data['x'], logr.predict_proba(data[['x']])[:,1], label='Logistic Regression') # 添加图例和标题 plt.legend() plt.title('Linear Regression vs Logistic Regression') # 显示图表 plt.show()

这个数据集包含一个连续的特征 x 和一个二元的目标变量 y。我们为 x 添加了一些正态分布的噪声，然后用一个阈值（在这个例子中是5）来决定 y 的值。因此，我们的目标是尝试预测给定 x 的情况下 y 的值。

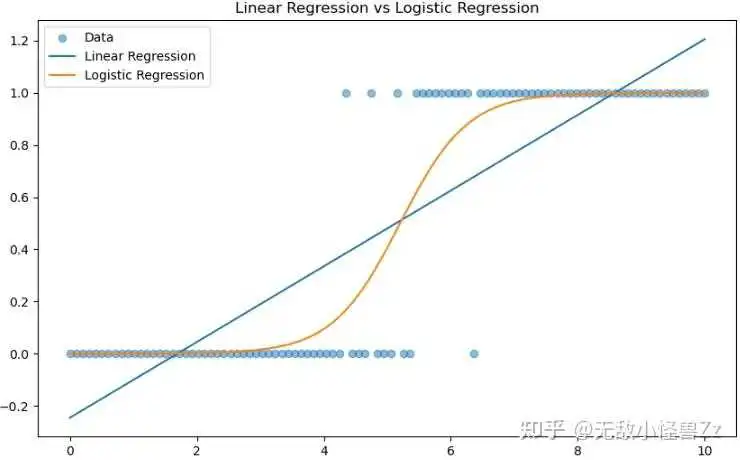
在这个图形中，横坐标代表特征 x，纵坐标代表目标变量 y。我们可以看到目标变量 y 只有两个值：0 或 1。这是一个典型的二元分类问题。

散点代表我们的原始数据。而两条线则是我们利用线性回归和逻辑回归得到的模型的预测结果。

线性回归的预测结果是一条直线，预测值可以在负无穷到正无穷的范围内取值。这在预测连续变量，如房价、销售额等问题时非常合适。然而，对于分类问题（目标变量只能取有限个离散值的问题），线性回归可能会预测出一些不合理的结果。例如，在这个图形中，线性回归的预测值在一些地方小于0或大于1，这对于我们的目标变量来说是不可能的。

逻辑回归的预测结果是一条形状类似于"S"的曲线，预测值始终在0到1之间。这个值可以被解释为属于正类（y=1）的概率。在特征 x 较小的时候，预测的概率接近于0，而在特征 x 较大的时候，预测的概率接近于1。这符合我们对分类问题的预期，因此逻辑回归更适合于处理这类问题。

虽然线性回归和逻辑回归都可以用于预测，但是它们各自适合于处理不同类型的问题：线性回归适合于预测连续变量，而逻辑回归适合于预测分类变量。

我们使用以下代码，创建一组数据集:

import numpy as np import matplotlib.pyplot as plt import pandas as pd # 设置随机数种子以保证结果可复现 np.random.seed(109) # 生成第一类点（比如标签为0） num_samples = 5 x0 = np.random.normal(2, 1, (num_samples, 2)) # 平均值为2，标准差为1的正态分布 y0 = np.zeros(num_samples) # 标签为0 # 生成第二类点（比如标签为1） x1 = np.random.normal(4, 1, (num_samples, 2)) # 平均值为4，标准差为1的正态分布 y1 = np.ones(num_samples) # 标签为1 # 合并两类点 X = np.concatenate((x0, x1)) Y = np.concatenate((y0, y1)) # 创建 DataFrame df = pd.DataFrame(np.concatenate((X, Y.reshape(-1, 1)), axis=1), columns=['x1', 'x2', 'y']) # 打印 DataFrame print(df) # 绘制图像 plt.figure(figsize=(4, 2)) plt.scatter(X[:, 0], X[:, 1], c=Y) plt.xlabel('x1') plt.ylabel('x2') plt.show()

这段代码的主要目标是创建并可视化一个二维的二分类数据集。

首先，通过正态分布生成了两类点，并分别标记为 0 和 1。接着，将这两类点以及对应的标签合并成完整的数据集，并存储在一个 pandas DataFrame 中。最后，通过 matplotlib 生成一个散点图，可视化了这两类点的分布，其中点的颜色对应其标签。我们来看一下输出和散点图

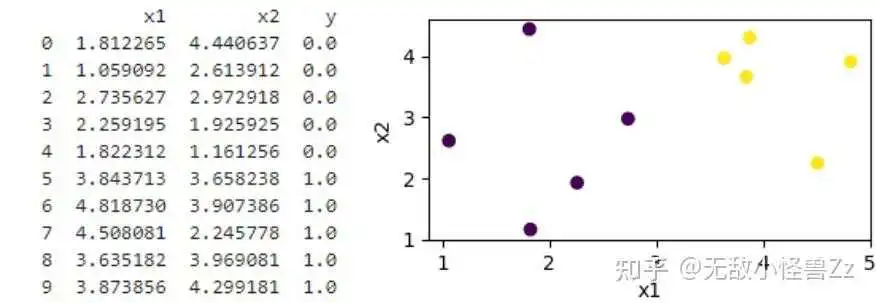
使用以下逻辑回归模型公式来预测输出值 $\hat{y}$ ：

$\hat y = \frac{1}{1 + e^{-(w_0 + w_1x_1 + w_2x_2)}} \\$

其中， $\hat{y}$ 是我们模型预测的概率输出，即y的概率。而 $w_0, w_1, w_2$ 是我们模型的参数，需要通过训练数据来学习。为了找到最佳的模型参数，我们通常使用梯度下降算法来最小化逻辑回归的损失函数（如交叉熵损失），这两方面的内容我会在下一篇中讲到，此处我先给出这三个参数值：

$w_0 = -5.91, w_1 = 1.43, w_2 = 0.46$

这意味着模型的形式为： $\hat y = \frac{1}{1 + e^{-(-5.91 + 1.43x_1 + 0.46x_2)}} \\$

我们使用代码进行计算：

w0 = -5.91 w1 = 1.17 w2 = 0.46 # 计算z值 z = w0 + w1 * df["x1"] + w2 * df["x2"] # 将z值代入sigmoid函数得到预测概率 y_hat = 1 / (1 + np.exp(-z)) # 打印出每个样本的预测概率 for i in range(len(y_hat)): print(f"样本{i+1}的预测概率是：{y_hat[i]:.4f}")

计算概率输出如下：

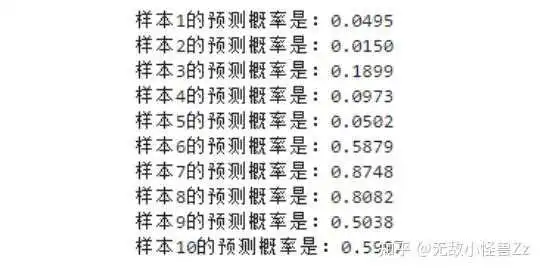
所以我们更新一下目前的数据情况：

样本	x1	x2	y	预测概率
1	1.	4.	0.0	0.1484
2	1.059092	2.	0.0	0.0302
3	2.	2.	0.0	0.2072
4	2.	1.	0.0	0.0846
5	1.	1.	0.0	0.0376
6	3.	3.	1.0	0.5671
7	4.	3.	1.0	0.8213
8	4.	2.	1.0	0.5981
9	3.	3.	1.0	0.5421
10	3.	4.	1.0	0.6457

逻辑回归的输出是(0,1)之间的连续型数值，也就是上面表格中的预测概率这一列，我们需要确定一个"阈值"，将其转化为二分类的类别判别结果，一般"阈值"取0.5，即：

$\begin{equation} \hat y=\left\{ \begin{aligned} 0, 预测概率<0.5 \\ 1, 预测概率≥0.5 \end{aligned} \right. \end{equation} \\$ 我们继续使用代码来实现这个过程，并进行绘图

import matplotlib.pyplot as plt import numpy as np # 设置阈值 threshold = 0.5 # 根据阈值进行分类 y_hat = (y_hat >= threshold).astype(int) # 创建一个画布，宽度为14，高度为6 fig, axes = plt.subplots(1, 2, figsize=(14, 6)) # 在左侧的图中绘制真实的标签情况 axes[0].scatter(df['x1'][df['y'] == 0], df['x2'][df['y'] == 0], color='blue', label='Label 0') axes[0].scatter(df['x1'][df['y'] == 1], df['x2'][df['y'] == 1], color='red', label='Label 1') axes[0].set_title('Actual Labels') axes[0].legend() # 在右侧的图中绘制预测的标签情况 axes[1].scatter(df['x1'][y_hat == 0], df['x2'][y_hat == 0], color='blue', label='Predicted Label 0') axes[1].scatter(df['x1'][y_hat == 1], df['x2'][y_hat == 1], color='red', label='Predicted Label 1') axes[1].set_title('Predicted Labels') axes[1].legend() # 显示图像 plt.show()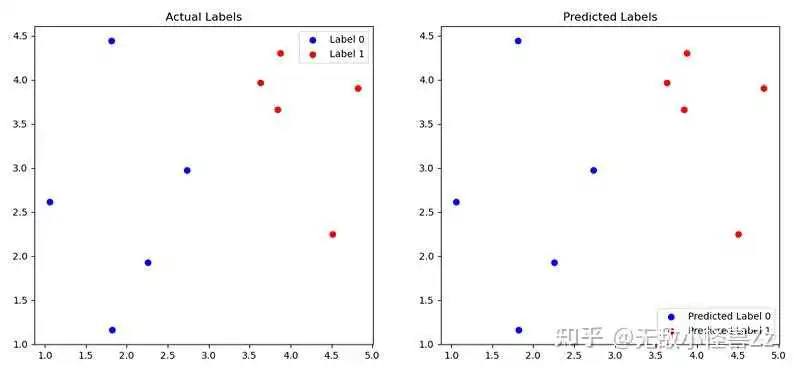

这两个图像是逻辑回归模型的真实值与预测值的散点图。

左图显示了样本的真实类别。蓝色的点代表类别0，红色的点代表类别1。可以看到，两类样本在x1和x2的分布上有一定的区别，这是我们应用逻辑回归模型进行分类的基础。

右图显示了模型的预测结果。同样的，蓝色的点代表预测为类别0，红色的点代表预测为类别1。通过比较左右两图，你可以看到预测结果大致上和真实情况是一致的。这说明模型在这组数据上的表现是良好的。

总结一下逻辑回归的建模过程：

在逻辑回归中，我们不仅预测出一个类别标签(0或1)，而且还预测出样本属于每个类别的概率，这种概率的预测是通过逻辑函数(Sigmoid)函数来实现的，具体的：

数学上，逻辑回归模型首先计算出一个线性函数的值，即： $z = w_0 + w_1x_1 + w_2x_2 + ... + w_nx_n + b \\$ 然后，这个线性函数的值 $z$ 被带入到sigmoid函数中，得到预测概率 $\hat y$ : $\hat y = \frac{1}{1 + e^{-z}} \\$ 这个预测概率 $\hat y$ 即为样本被预测为类别1的概率，它的值在(0，1)之间。

最后，我们可以设定一个阈值(一般是0.5)，如果 $\hat y$ 大于等于这个值，那么我们就预测这个样本为类别1，否则预测为类别0。这就是我们上述实现的过程。

在上述的模拟数据中，我直接给出了 $w_0,w_1,w_2$ 的值，实际上这些模型参数的值是通过机器学习算法从数据中学习得到的，逻辑回归模型通常使用梯度下降（Gradient Descent）或其他优化算法来找到能够使损失函数最小的参数值。损失函数的选择通常为交叉熵损失（Cross-Entropy Loss），接下来的文章将会有参数估计和梯度下降的详细解读，届时我们就能够很好的理解如何得到最优的超参数以完成完整的逻辑回归建模。

最后，感谢您阅读这篇文章！如果您觉得有所收获，别忘了点赞、收藏并关注我，这是我持续创作的动力。您有任何问题或建议，都可以在评论区留言，我会尽力回答并接受您的反馈。如果您希望了解某个特定主题，也欢迎告诉我，我会乐于创作与之相关的文章。谢谢您的支持，期待与您共同成长！

期待与您在未来的学习中共同成长。

森林图目前在相关文献中可以说是非常常见了，不只是亚组分析中，普通的回归分析结果也可以用森林图进行可视化展示，不仅可以帮助我们更好地理解不同变量间的一致性和差异性，新颖的图片还能为文章增色不少。

当下主流绘制森林图的方式还是R语言，其他也有使用GraphPad Prism或者excel，但就R语言而言，一行行的代码参数着实让人头大，不仅需要一定的代码基础，想要画出好看的森林图，参数也要调上好久，效率着实是低了一些......

# 定义一个简单的主题，大家可以随意发挥自己的审美！ tm <- forest_theme(base_size = 10, # 设置基础字体大小 refline_col = "red4", # 设置参考线颜色为红色 arrow_type = "closed", # 设置箭头类型为闭合箭头 footnote_col = "blue4") # 设置脚注文字颜色为蓝色 # 绘制森林图 p <- forest(result2[,c(1, 2, 9, 6)], # 选择要在森林图中使用的数据列，这里包括变量名列、患者数量列、绘图要用的空白列和HR（95%CI）列 est = result2$HR, # 效应值，也就是HR列 lower = result2$lower.95, # 置信区间下限 upper = result2$upper.95, # 置信区间上限 sizes = result2$se, # 黑框框的大小 ci_column = 3, # 在第3列（可信区间列）绘制森林图 ref_line = 1, # 添加参考线 arrow_lab = c("Low risk", "High Risk"), # 箭头标签，用来表示效应方向，如何设置取决于你的样本情况 xlim = c(-1, 10), # 设置x轴范围 ticks_at = c(-0.5, 1, 3, 5, 7), # 在指定位置添加刻度 theme = tm, # 添加自定义主题 footnote = "This is the demo data. Please feel free to change\nanything you want.") # 添加脚注信息 p # 加列P值 p <- forest(result2[,c(1, 2, 9, 6, 7)], # 加了P值列哟！选择要在森林图中使用的数据列，这里包括变量名列、患者数量列、绘图要用的空白列和HR（95%CI）列 est = result2$HR, # 效应值，也就是HR列 lower = result2$lower.95, # 置信区间下限 upper = result2$upper.95, # 置信区间上限 sizes = result2$se, # 黑框框的大小 ci_column = 3, # 在第3列（可信区间列）绘制森林图 ref_line = 1, # 添加参考线 arrow_lab = c("Low risk", "High Risk"), # 箭头标签，用来表示效应方向，如何设置取决于你的样本情况 xlim = c(-1, 10), # 设置x轴范围 ticks_at = c(-0.5, 1, 3, 5, 7), # 在指定位置添加刻度 theme = tm, # 添加自定义主题 footnote = "This is the demo data. Please feel free to change\nanything you want.") # 添加脚注信息 p

现在郑老师风暴统计平台，可以自动画出森林图了！！！！回归分析后，不需要额外撰写代码，自动绘制出森林图！！！不需要写代码！！！

NEJM:

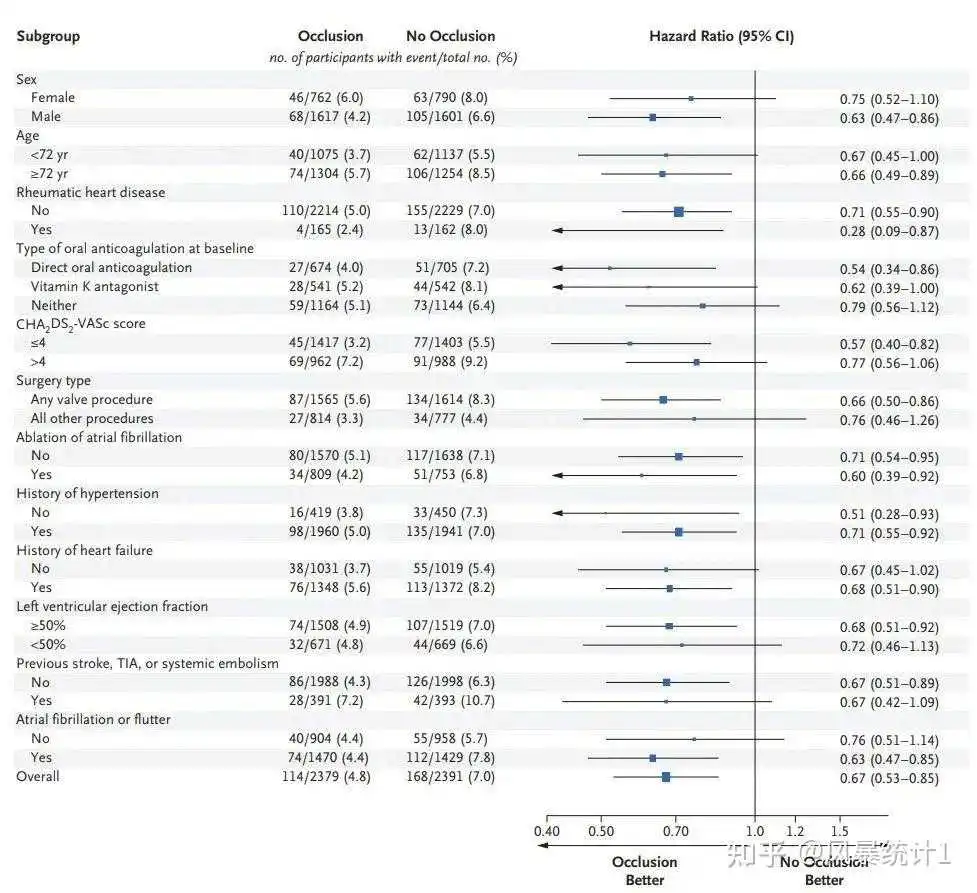
详情请点击下方：

现在可以自动产生影响因素森林图了！ (.com)

到此这篇sigmoid函数和logistic（sigmoid和logistic的区别）的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章，希望大家都能在编程的领域有一番成就！

上一篇： docker网络模型（docker4种网络模式）

下一篇：反激占空比计算公式（反激占空比）

版权声明：
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/54399.html

相关文章：