convwthn函数（conv()函数）



1 autograd

从昨天的线性回归例子来看，反向传播需要手动实现，这对于线性回归等较简单的模型来说，还可以对应，但对于非常复杂的网络结构，手动实现反向传播，不仅费时费力，而且容易出错，难以检查。

torch.autograd就是为了方便用户使用，开发的自动求导引擎，能够输入和前向传播自动构建计算图并实现反向传播

计算图(Computation Graph)是现代深度学校框架的的科学，高相的自动求导算法-反向传播提供了理论支持

1.1requires_grad

可以认为需要求导(requires_grad)的tensor即Variable.autograd记录对tensor的操作用来构建计算图

variable.backward(gradient = None,retain_graph = None,create_graph = None)主要有以下参数

a = t.randn(3,4, requires_grad=True)#在创建的时候指定需要求导

->tensor([[ 0.1718, -0.0656, 2.0948, 0.3005], [-1.5047, 1.3276, 0.9747, -1.3517], [-0.7178, -1.1574, 0.1886, 0.6724]], requires_grad=True)#输出的时候会多一个小尾巴

尝试手动定义函数的导数

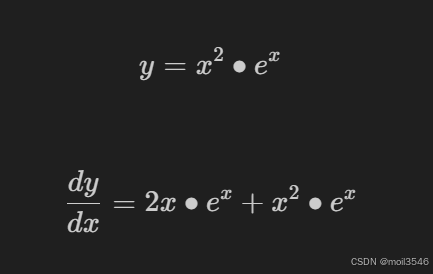
def f(x):

    '''计算y'''

    y = x2 * t.exp(x)

    return y

def gradf(x):

    '''手动求导函数'''

    dx = 2*x*t.exp(x) + x2*t.exp(x)

    return dx

让我们来看一下这两组的误差

x = t.randn(3,4, requires_grad = True)

y = f(x)

y

->tensor([[3.5210e-01, 3.1778e-02, 3.9708e+00, 8.9039e-02], [9.1834e-03, 1.3747e+01, 3.2083e+01, 1.0472e-02], [3.6645e-02, 2.5477e+01, 3.4921e-03, 4.5742e-01]], grad_fn=<MulBackward0>)#将x中的每一个数放进去做了个新的tensor(未求导)

 y.backward(t.ones(y.size()))#使得gradient的形状给和y一致，手动指定使用的梯度，使得y对x的梯度能够计算，y.backwar（）d的方法常用于计算y对于输入x的梯度，当y是一个张量时，需要未每个元素指定一个权重，这就是为什么利用t.ones(y.size())给每个y元素分配了1的权重

x.grad#由于设定了requires_grad = True ，pytorch会为x跟踪所有计算操作，并在反向传播时计算梯度，并储存在x.grad中

->tensor([[ 2.6500e+01, 1.2230e+00, 3.4075e+00, 3.9616e+01], [-4.3179e-01, -3.4538e-01, 1.4072e+02, 8.8669e-01], [ 3.0257e+01, -1.3991e-01, 4.9397e+00, -4.5476e-01]])#输出的就是求导后y，带入各个x的值

gradf(x)

->tensor([[ 2.6500e+01, 1.2230e+00, 3.4075e+00, 3.9616e+01], [-4.3179e-01, -3.4538e-01, 1.4072e+02, 8.8669e-01], [ 3.0257e+01, -1.3991e-01, 4.9397e+00, -4.5476e-01]], grad_fn=<AddBackward0>)

两种方法一致

1.2计算图

pytorch 中的底层采用了计算图，一种特殊的有响五环图，用于记录算子与变量之间的关系

矩形表述算子，椭圆表示变量

z = wx+b 可分解为y = wx 和z = y+b

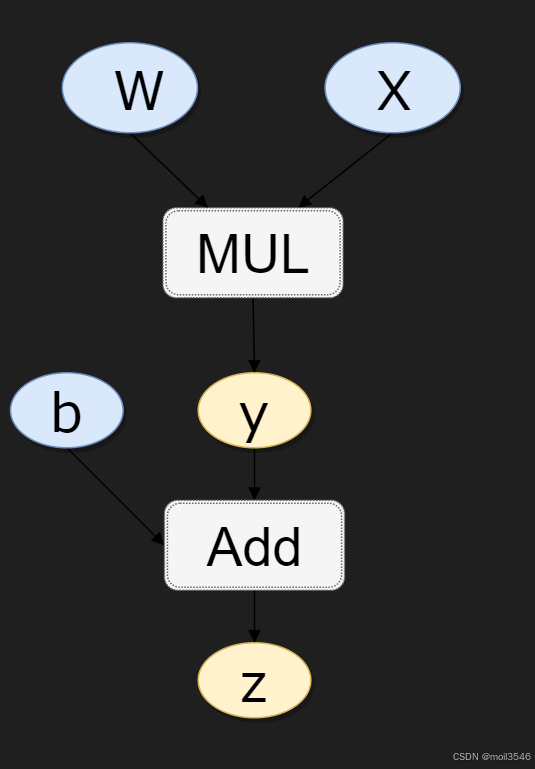
MUL合ADD都是算子，b,w,x都是变量

同时x，b时叶子节点，这类节点通常由自己创建，不依赖其他变量，z称为根节点，是计算图的最终目标，利用链式法则很容易求得各个节点的梯度

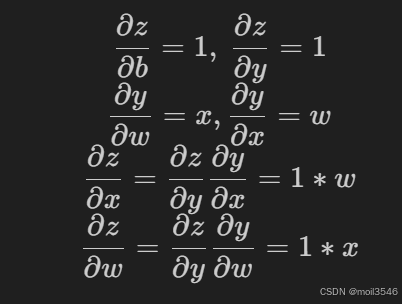
而有了计算图，上述链式求导即可利用计算图的反向传播自动完成

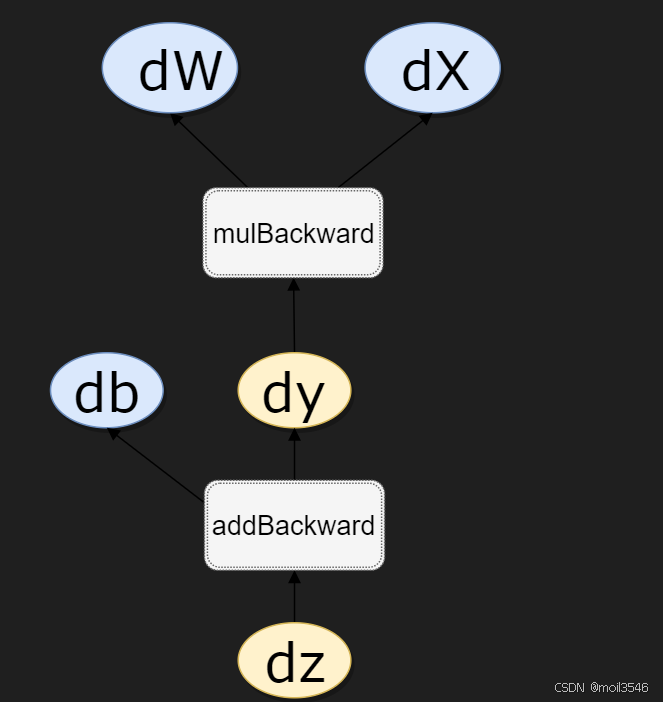
在pytorch的实现过程中，autograd会虽赊用户的操作，记录当前的操作，并建立一个有向无环图，用户每进行一个操作，计算图就会发生变化

在反向传播的过程中，autograd就是沿着当前变量（根节点z）溯源，并利用链式求导法则计算所有叶子节点的梯度

每一个向前操作的函数都有对应的反向传播来计算输入的个variable的梯度

版权声明：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/36518.html