sigmoid函数求导（sigmoid函数求导范围）

题主观察能力很强啊，梯度形如（预测值 - 真值），这是指数族分布（exponential family）+ 正则关联函数（canonical link function）的一般结果。欢迎学习广义线性模型（Generalized Linear Model）：

https:// cedar.buffalo.edu/~srih ari/CSE574/Chap4/4.3.6-CanonicalLink.pdf
https:// blog.csdn.net/ITleaks/a rticle/details/

更多的资料可以看 Stanford CS229 的 notes 或者 PRML 中的相关章节。

其中几种比较常见的激活函数和损失函数的组合如下：

linear activation（就是没有激活函数） + square loss
sigmoid activation + cross entropy loss
softmax activation + multi-class cross entropy loss

问题思考

说到softmax和sigmoid二者差别，就得说说二者分别都是什么。其实很简单，网上有数以千计的优质博文去给你讲明白，我只想用我的理解来简单阐述一下：

sigmoid函数针对两点分布提出。神经网络的输出经过它的转换，可以将数值压缩到(0,1)之间，得到的结果可以理解成“分类成目标类别的概率P”。而不分类到该类别的概率，就是(1 - P)，这也是典型的两点分布的形式；

softmax本身针对多项分布提出，当类别数是2时，它退化为二项分布，而它和sigmoid真正的区别就在这儿——二项分布包含两个分类类别（姑且分别称为A和B）；而两点分布其实是针对一个类别的概率分布，其对应的那个类别的分布，直接由1-P粗暴得出。

据上所述，sigmoid函数，我们可以当作成它是对一个类别的“建模”。将该类别建模完成，另一个相对的类别就直接通过1减去得到；

而softmax函数，是对两个类别建模。同样的，得到两个类别的概率之和也是1.

问题解答

所以我到底要说个什么问题呢。。。（好像扯远了）我要说的是，神经网络在做二分类时，使用softmax还是sigmoid，做法其实有明显差别。由于softmax是对两个类别（正反两类，通常定义为0/1的label）建模，所以对于NLP模型而言（比如泛BERT模型），Bert输出层需要通过一个nn.Linear()全连接层压缩至2维，然后接softmax（pytorch的做法，就是直接接上torch.nn.CrossEntropyLoss）；而sigmoid只对一个类别建模（通常就是正确的那个类别），所以Bert输出层需要通过一个nn.Linear()全连接层压缩至1维，然后接sigmoid（torch就是接torch.nn.BCEWithLogitsLoss）

我们来看俩例子：

先看softmax的：

class AlbertForSequenceClassification(AlbertPreTrainedModel): def __init__(self, config): super(AlbertForSequenceClassification, self).__init__(config) self.num_labels = config.num_labels self.bert = AlbertModel(config) self.dropout = nn.Dropout(0.1 if config.hidden_dropout_prob == 0 else config.hidden_dropout_prob) self.classifier = nn.Linear(config.hidden_size, self.config.num_labels) self.use_weight = True if "use_weight" in config.__dict__.keys() else False self.init_weights() def forward(self, input_ids, attention_mask=None, token_type_ids=None, position_ids=None, head_mask=None, labels=None): outputs = self.bert(input_ids, attention_mask=attention_mask, token_type_ids=token_type_ids, position_ids=position_ids, head_mask=head_mask) pooled_output = outputs[1] pooled_output = self.dropout(pooled_output + 0.1) # 这里为啥+0.1? logits = self.classifier(pooled_output) # classifier其实就是个将312维压缩至2维的线性层 outputs = (logits,) + outputs[2:] # add hidden states and attention if they are here if labels is not None: if self.num_labels == 1: # We are doing regression loss_fct = MSELoss() loss = loss_fct(logits.view(-1), labels.view(-1)) else: class_weight = torch.FloatTensor([0.18, 0.82]) class_weight = class_weight.to('cuda') if self.use_weight: # 这里是我的个人改动，在ce上加了weight，无需关注。。。 ce = CrossEntropyLoss(class_weight) # 交叉熵损失在这里！要改损失函数在这儿改！ loss = ce(logits.view(-1, self.num_labels), labels.view(-1)) else: # 对于一般分类任务而言，计算Loss在这里 loss_fct = CrossEntropyLoss() loss = loss_fct(logits.view(-1, self.num_labels), labels.view(-1)) outputs = (loss,) + outputs return outputs # (loss), logits, (hidden_states), (attentions)

熟悉的同学一眼便知，这个例子来自老版huggingface/transformer库的modeling_albert.py文件，没记错的话，当时该库叫pytorch_pretrained_bert，现如今以及被改的面目全非了，各种封装让人欲仙欲死，但好在有其他大佬保留了原本简单易懂的代码，链接放在这儿

见code line7，此处定义self.classifier = nn.Linear(config.hidden_size, self.config.num_labels)，其中self.config.num_labels=2。而后面计算Loss使用了包装了logSoftmax和NLLLoss的CrossEntropyLoss，即使用softmax时，最后的线性层将维度压缩至2维。

再看看sigmoid

 def _get_discriminator_output(self, inputs, discriminator, labels): """Discriminator binary classifier.""" with tf.variable_scope("discriminator_predictions"): hidden = tf.layers.dense( discriminator.get_sequence_output(), units=self._bert_config.hidden_size, activation=modeling.get_activation(self._bert_config.hidden_act), kernel_initializer=modeling.create_initializer( self._bert_config.initializer_range)) logits = tf.squeeze(tf.layers.dense(hidden, units=1), -1) # dense-layer输出维度是1 weights = tf.cast(inputs.input_mask, tf.float32) labelsf = tf.cast(labels, tf.float32) losses = tf.nn.sigmoid_cross_entropy_with_logits( # 这里采用了sigmoid以及它对应的Loss函数 logits=logits, labels=labelsf) * weights per_example_loss = (tf.reduce_sum(losses, axis=-1) / (1e-6 + tf.reduce_sum(weights, axis=-1))) loss = tf.reduce_sum(losses) / (1e-6 + tf.reduce_sum(weights)) probs = tf.nn.sigmoid(logits) preds = tf.cast(tf.round((tf.sign(logits) + 1) / 2), tf.int32) DiscOutput = collections.namedtuple( "DiscOutput", ["loss", "per_example_loss", "probs", "preds", "labels"]) return DiscOutput( loss=loss, per_example_loss=per_example_loss, probs=probs, preds=preds, labels=labels,)

该例子来自于google/electra，源码链接在此，对模型感兴趣的同学可见：ELECTRA论文阅读笔记

从该代码的line 10可见，ELECTRA判别器（可看作一个专做二分类任务的BERT model）的输出被tf.layers.dense压缩成1维；然后再在line 13，模型使用了tf.nn.sigmoid_cross_entropy_with_logits。

总结

总而言之，sotfmax和sigmoid确实在二分类的情况下可以化为相同的数学表达形式，但并不意味着二者有一样的含义，而且二者的输入输出都是不同的。sigmoid得到的结果是“分到正确类别的概率和未分到正确类别的概率”，softmax得到的是“分到正确类别的概率和分到错误类别的概率”。

一种常见的错法（其实就是我自己的错法），即，错误地将softmax和sigmoid混为一谈，在把BERT输出层压缩至2维的情况下，却用sigmoid对结果进行计算。这样我们得到的结果其意义是什么呢？

假设我们现在BERT输出层经nn.Linear()压缩后，得到一个二维的向量：

[-0.81787, 1.9287]

对应类别分别是(0,1)。我们经过sigmoid运算得到：

tensor([0.2805, 0.8748])

前者0.2805指的是分类类别为0的概率，0.8748指的是分类类别为1的概率。二者相互独立，可看作两次独立的实验（显然在这里不适用，因为0-1类别之间显然不是相互独立的两次伯努利事件）。所以显而易见的，二者加和并不等于1.

若用softmax进行计算，可得：

tensor([0.0529, 0.9471])

这里两者加和是1，才是正确的选择。

假设存在A、B两个类别，它们类别的最终输出值为a和b。以上计算得到的结果可以如下看待：

sigmoid：

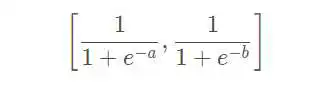
softmax:

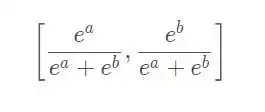
差别还是很明显的

所以，这两者之间确实有差别，而softmax的处理方式，有时候会得到相较于sigmoid处理方式的微小提升。

————————————————

原文链接：浅谈sigmoid函数和softmax函数_甘如荠-CSDN博客

重新认识注意力：为什么有的神经网络加入注意力机制后效果反而变差了？

softmax：常用与单标签分类，解决只有唯一正确答案的问题时，加权求和值为1。是常用注意力机制self-attention、SKNet的激活函数。

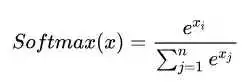
softmax可以当作arg max的一种平滑近似，与arg max操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。

sigmoid：常用与多标签分类，它将任意的值转换到0-1之间，是常用注意力SE、CBAM的激活函数。

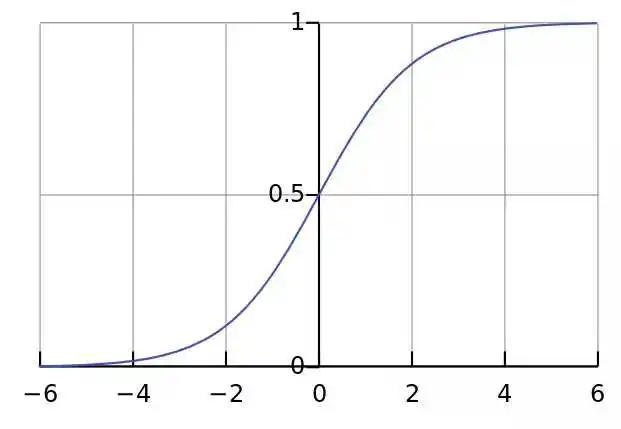
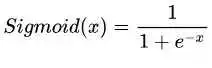
缺点：1. 最明显的就是饱和性，从上图也不难看出其两侧导数逐渐趋近于0，容易造成梯度消失。2.激活函数的偏移现象。Sigmoid函数的输出值均大于0，使得输出不是0的均值，这会导致后一层的神经元将得到上一层非0均值的信号作为输入，这会对梯度产生影响。3. 计算复杂度高，因为Sigmoid函数是指数形式。

对注意力来说，虽然都将输出激活到0-1，但softmax更离散，sigmoid更加均衡（训练经常打印结果的朋友应该发现，在网络学习不到东西时，softmax通常会全部学习到一个类别上，全1。而sigmoid一般导致所有预测都是0.5）。对中间的特征层来说，对特征图全部施加一个0.5大小的权重，即使学不好影响也不会很大，但用softmax，如果关键特征学不好，大权重必然会落到无用特征上，也就造成了负面影响。且softmax的影响是持续性的，若出初始时学不好，很可能导致注意力权重对应的整幅特征图始终都学不好（若初始时给到一个较小的权重，那么网络很可能不再对该组特征的进行学习，即使该特征的学习对最终任务的贡献很大，也很难对网络输出造成影响，类似的详细说明可参考文章Dynamic Convolution: Attention over Convolution Kernels）

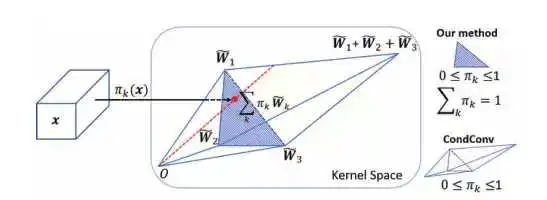
那是不是可以说明sigmoid就比softmax好呢？

不见得，sigmoid比softmax易学，但如果都能学好，softmax是比sigmoid要好的，用softmax是为了区分，sigmoid能够保底。

因此，当有大量注意力权重需要优化时，用sigmoid，如SE、CBAM等，或者用改进的softmax；当需要特别区分特征之间差别或网络学有余力的时候用softmax，如轻量化网络、分类层；当然，还有一些加权和要为1的要用softmax，如SKnet。

那么self-attention为什么不用sigmoid呢？

仔细研究transformer会发现，它里面有个特征平滑的操作，这间接将softmax改进成了如下的样子：

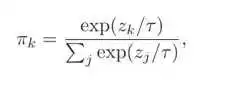
使得softmax的激活更加平滑，更易学习。

最后，每种注意力机制都需要考虑各种设计细节，包括注意力权重的产生方式、注意力的作用方式、注意力的提升原理，才能更好发挥注意力的作用。

sigmoid是开关，softmax是平均，两个作用是不同的。

Attention是注意力的意思，该机制中一般包含了两个关键点：（1）产生attention map，在cbam中是一张图或者是一个向量，在self-attention中是相关度矩阵；（2）将attention map与原图结合，产生attention激活后的结果。在cbam中是哈达玛积，在self-attention是矩阵乘法。激活函数的设计与（1）有关，这里提供一个步骤，根据该步骤能够明确attention map的设计方法。

确认attention主体，也即attention map的形式，也即要关注什么？
attention map的极端情况。假设我们人为地为每个样本提供一个attention map，是怎样的情况？比如cbam的空域注意力，我就想在有物体的地方套上全1的mask，其余地方全部设为0。
设计原特征到attention map的映射关系，还是以cbam为例，我们知道，通常可以用激活图来代表该某位置是否存在物体，通过卷积的方式将其降维之后得到attention map，这个应该是我们在步骤2中提到的map的软化版本，所以我们对最后加以sigmoid得到最后结果。
最后，检查attention结果的数值范围，一般输入输出的数值范围是一致的，同样在cbam中，由于原图乘以的数字在[0,1]之内，所以不会出现数值爆炸的情况，对于最为重要的区域，由于attention map的数值为1，所以数值范围得到了保护。

Discussion：这个例子中，能不能用softmax？表达意义上：不太好，因为softmax带有竞争意味，若是在空域上做softmax，会使得map过于集中于某一点，反而使得attention效果下降；数值范围上：数值范围会限制减小不适合。

什么时候用softmax小技巧：通常，当softmax出现的时候，基本能找到这个形式：sum(wi * xi),i=0,1,...n，其中softmax作用于wi上。

你到底是要做每个维度的二分类，还是要做全维度的多分类，这个问题必须先搞清楚。

注意力之所以叫注意力，就是因为你有些地方不注意，才能显得有些地方在“注意”。

而softmax其实可以看做一个正则化过程，也就是输出的数值总和为1。

你如果用SIGMOD，就不是在做正则化和注意力调整。SIGMOD的灵活度也更高，可以让“注意力”变成“什么都注意机制”或者“什么都不注意机制”。

SIGMOD做出来的transformer其逻辑更类似观察机制。也就是“看没看”，而不是“注意不注意”

用sigmoid叫gating

用softmax才叫attention

softmax是为了在不同token之间互相竞争注意力。如果改用mean(sigmoid(x))，那么每个token吸引的注意力就互相独立，不会受到别的token的直接影响。

这样做说不定真的可行。因为目前的看法是 softmax 其实不太对，当所有 token 的激活程度都很低时会出现异常数值，参见 Attention Is Off By One 。目前主流观点是改用 softmax1，或者依赖bos token来防止异常数值。

我也不知道具体是softmax1更好，还是mean(sigmoid(x))更好。但我有些猜测。

目前大模型测试长注意力的性能会用大海捞针实验，比如：

https:// arxiv.org/html/2404.066 54v2

当需要找出多根针时，softmax transformer的多根针会竞争注意力，可能会导致某些针被忽略。mean sigmoid transformer理论上在多根针的大海捞针实验里会有一些优势。

再想想，如果用sigmoid，那这不就是个激活函数吗？能不能把sigmoid换成ReLU系的函数？

但是mean ReLU transformer的缺点是k和v都变成简单的乘法了，就类似MPL了。这还能叫transformer吗？有没有可能把两种做法结合一下，只删掉一部分宽度的k，让对应的这部分v直接和q相乘然后调个element-wise的激活函数，剩下宽度的k保留，还是用softmax？

有没有大佬愿意做个实验验证一下mean sigmoid/ReLU transformer行不行？

還真有人直接用 sigmoid 取代 softmax [1]，不過這個 sigmoid 需要 bias term，代碼開源在 GitHub 上（https://github.com/apple/ml-sigmoid-attention）。我有點不敢相信竟然做法這麼簡單……

$\mathrm{SigmoidAttn}(\mathbf{X}) = \sigma(\frac{\mathbf{Q}\mathbf{K}^{\mathrm{T}}}{\sqrt{d_{k}}})\mathbf{V}$

其中， $\sigma(x) = \frac{1}{1+\exp(-(x+b))}$ 是 sigmoid with bias term ，

作者建議 $b = -\log{n}$ 。

[1] Jason Ramapuram, Federico Danieli, Eeshan Dhekane, Floris Weers, Dan Busbridge, Pierre Ablin, Tatiana Likhomanenko, Jagrit Digani, Zĳin Gu, Amitis Shidani, & Russ Webb (2024). Theory, Analysis, and Best Practices for Sigmoid Self-Attention. arXiv preprint arXiv: 2409.04431.

大模型时代来答：经过优化的Sigmoid Attention正在冒头，要让它稳定训练、匹敌Softmax的效果，只需要把bias项b初始值设成一个较大的负值。

首先回顾Sigmoid的基本性质。在Sigmoid Attention中，每个位置的注意力分数与其他位置的结果无关，不像Softmax Attention那样受归一化约束，充分并行后计算效率更高，但也正是因为没有归一化约束，Sigmoid Attention中某些位置的注意力分数容易变得很大，训练效果往往不如softmax attention。

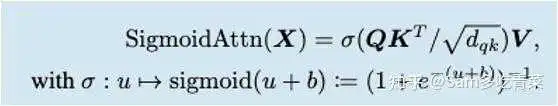
因为效果问题，目前大部分语言、视觉预训练模型用的都还是Softmax Attention，不过最近Apple的一篇技术报告最近重新发掘了Sigmoid Attention的潜力。

划重点：原始的Sigmoid Attention存在训练不稳定、效果差于Softmax Attention的问题，但只要对注意力分数的norm进行适当的正则化，效果就与Softmax Attention基本相当，而且显著快于Softmax Attention。下面详细来看。

论文：Theory, Analysis, and Best Practices for Sigmoid Self-Attention 链接

实验观察：如下图，作者发现用传统的三角位置编码和ROPE位置编码训的Sigmoid Attention LM效果都不如Softmax版本，但如果使用Alibi位置编码，也就对Attention分数减去一个Bias项使之接近0，训练效果就与Softmax相近。

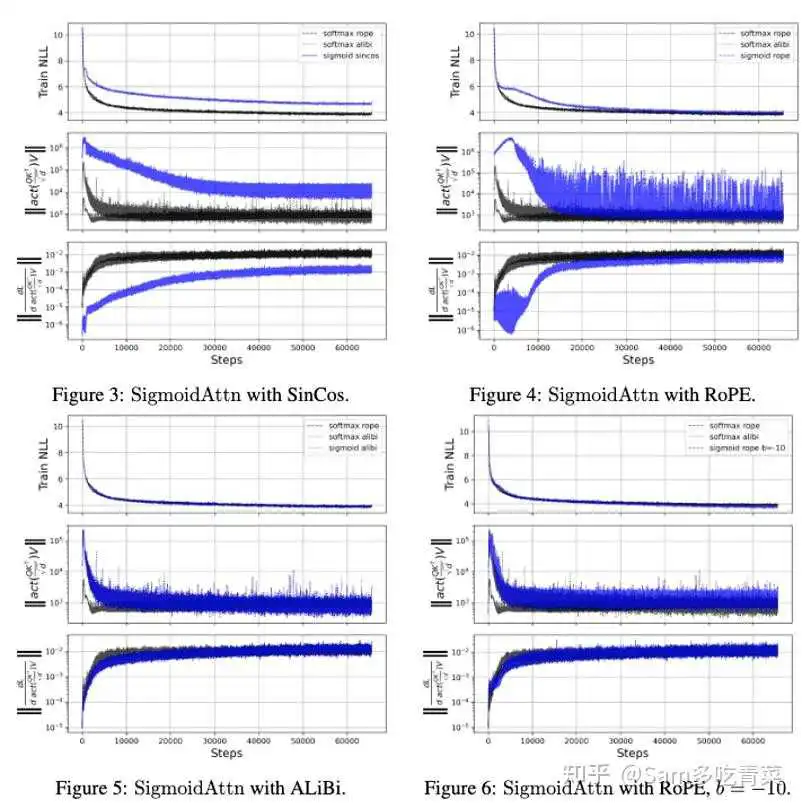
方法：从上述观察可以发现，约束Sigmoid Attention注意力分数的范数大小就可以稳定其训练，可以用Alibi位置编码，也可以对sigmoid的bias项b赋一个大的初始负值，作者用的是-ln(n)（n为序列长度），加上对b的初始化约束后，用ROPE的模型就可以正常训练（上图右下角）。

实验：

1️⃣训练效果终于匹敌Softmax Self Attention：如下图，在1B参数量的Llama预训练、ASR预训练、ViT的MAE/SimCLR/BYOL/有监督预训练上都与Softmax版本相当。

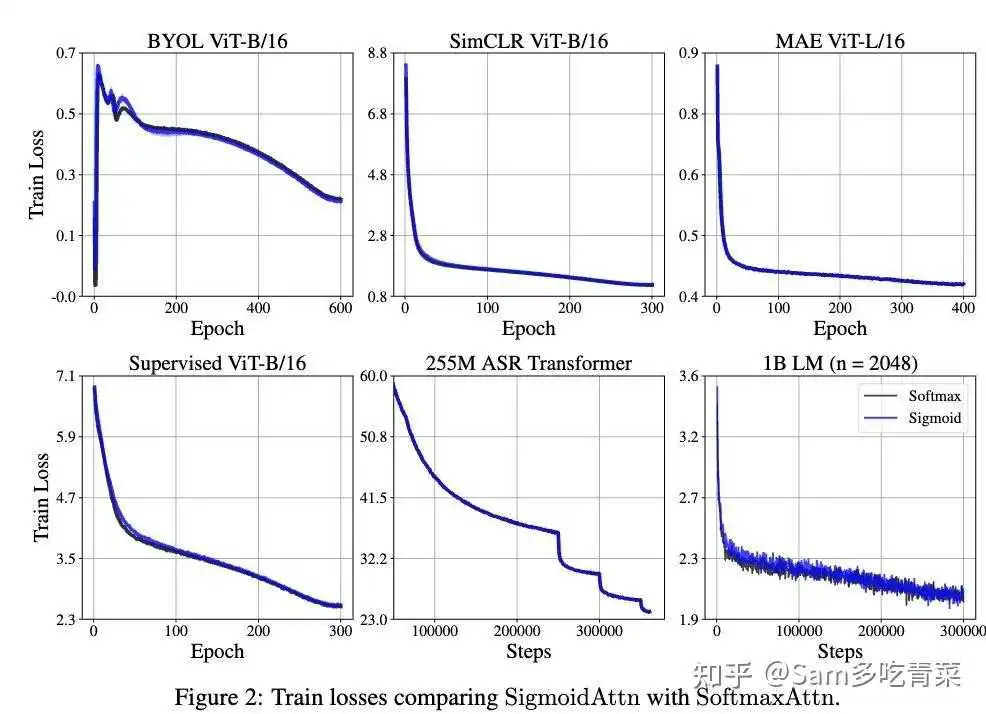
2️⃣显著加速：作者对标Flash-Attention设计了sigmoid版本的kernel，如p3，在64-78k的序列长度上，self-attention推理比softmax快17.39%、训练快6.53%，causal attention推理比softmax快18.76%、训练快9.46%。

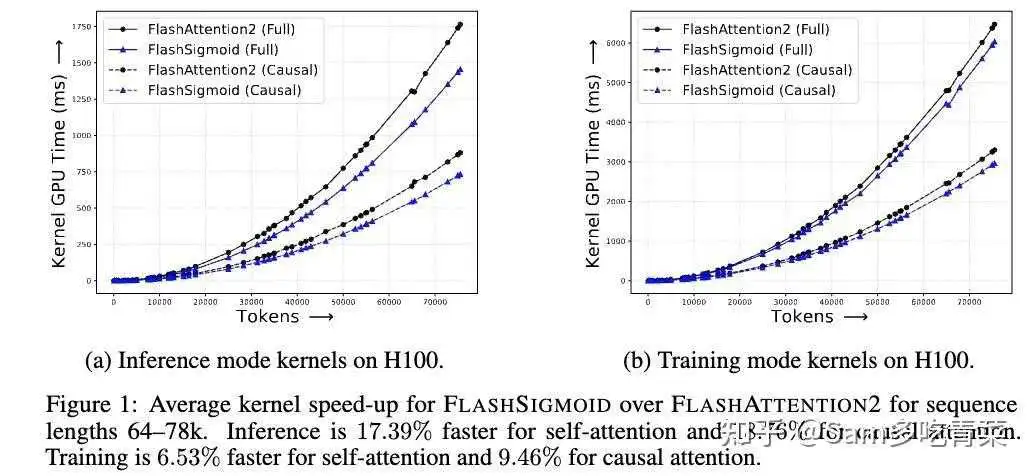
期待社区在这篇工作的基础上继续探究Sigmoid Attention的scaling性质，如果有好用的Sigmoid Attention大模型出现，或许Sigmoid激活会像在SigLIP中代替CLIP的Softmax输出层激活那样，逐渐在Transformer的Attention中取代Softmax。

我是 @Sam多吃青菜，北大本硕毕业的NLPer/大厂高级算法工程师，日常更新LLM和深度学习领域前沿进展，也接算法面试辅导，欢迎关注和赐读往期文章，多多交流讨论^_^。附带一波往期干货内容：

为什么现在的LLM都是Decoder only的架构？为什么在设置 model.eval() 之后，pytorch模型的性能会很差？Sam多吃青菜：大模型微调新范式：当LoRA遇见MoE如何评价 ACL 2024 / February ARR cycle 结果？如何看待视觉多模态大模型的爆炸式的发展？在用llava架构训vlm时，llm基模选择base模型好还是chat模型好呢？深度学习硕士毕业论文工作量不够怎么办？论文简读第37期：You Only Cache Once: D…如何评价微软发布的 phi-3？Sam多吃青菜：算法冷知识第1期-大模型的FFN有什么变化？Sam多吃青菜：算法冷知识第2期-一文看遍节省显存技巧（附代码）Sam多吃青菜：算法冷知识第3期-1B参数的大模型训练需要多少显存？Sam多吃青菜：算法冷知识第4期-LoRA为什么能加速大模型训练？别想得太简单哦Sam多吃青菜：算法冷知识第5期——L2正则化和Weight Decay总是分不清？AdamW经典重温Sam多吃青菜：算法冷知识第6期——适合大模型训练的浮点格式BF16机器学习中有哪些形式简单却很巧妙的idea？NLP中有什么比较好的sentence/paragraph embedding方法？Sam多吃青菜：开卷翻到毒蘑菇？浅谈大模型检索增强（RAG）的鲁棒性Sam多吃青菜：LLaMA2+RLHF=脆皮大模型？ICLR 2024 高分投稿：多样性驱动的红蓝对抗深度学习调参有哪些技巧？Llama 3 发布，那些信息值得关注？Sam多吃青菜：大模型对齐的奇兵——黑盒 Prompt 优化BPOSam多吃青菜：个性有了，心眼坏了？大模型微调的潜在危害Transformer解码器推理速度慢怎么优化？现在的深度学习的模型越来越大，有个结论是说，大脑的激活是非常稀疏的，对模型参数有什么好的办法压缩吗?最近尝试搞求职辅导，模拟面试了好几位同…

#LLM #人工智能 #深度学习 #自然语言处理 #NLP #算法面试 #大模型 #ChatGPT

通过logistic曲线就可以知道

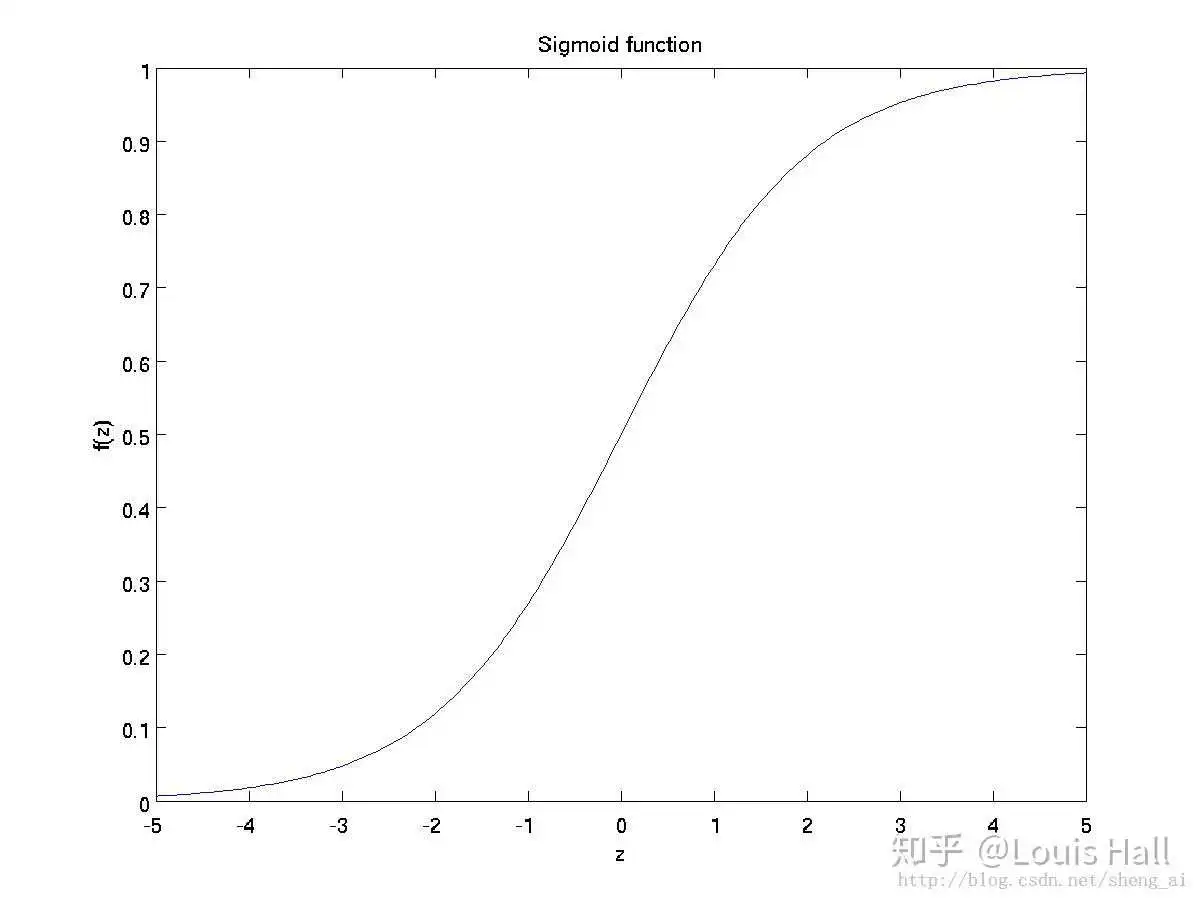
sigmoid函数的导数是以它本身为因变量的函数，即f(x)' = F(f(x))

sigmoid函数是一个阀值函数，不管x取什么值，对应的sigmoid函数值总是∈(0,1)

1、证明f(x)' = F(f(x)) $f'(x)=[\frac{1}{1+e^{-x}}]'=\frac{1'.(1+e^{-x})-1.(1+e^{-x})'}{(1+e^{-x})^{2}}=\frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x})^{2}}=\frac{1}{1+e^{-x}} (1-\frac{1}{1+e^{-x}})=f(x)[1-f(x)]$

所以 $f'(x)=F(f(x))$

sigmoid函数的值域∈(0,1)，这与概率值的范围[0,1]很是巧合，我们可以把sigmoid函数与一个概率分布联系起来，那就是伯努利分布。

伯努利分布的概率质量函数为： $f(x|p)=p^{x}(1-p)^{1-x}$

2、证明伯努利分布也属于指数分布族

指数分布族的一般表达式 $f(x|\theta)=h(x)e^{y(\theta)T(x)-A(\theta)}$

伯努利分布的概率质量函数为：

$f(x|p)=p^{x}(1-p)^{1-x}=e^{ln[p^{x}(1-p)^{(1-x)}]}=e^{[lnp^{x}+ln(1-p)^{1-x}]}=e^{[xln\frac{p}{1-p}+ln(1-p)]}$

由此可知，伯努利分析也是属于指数分布族

3、sigmoid函数的数学公式推导

由伯努利分布 $f(x|p)=p^{x}(1-p)^{1-x}$ 属于指数分布族

$y(\theta)=ln\frac{p}{1-p}$ ， $e^{y(\theta)}=\frac{p}{1-p}$ ， $(1-p)e^{y(\theta)}=p$ ， $p=\frac{e^{y(\theta)}}{1+e^{y(\theta)}}=\frac{1}{1+e^{-y(\theta)}}$

可知p的值域恒 $\in$ （0，1）

这篇文章首先讲了神经网络中为什么要引入激活函数，以及一个激活函数应该具有哪些性质。最后详细地对比了几种常见的激活函数的优缺点，重点讲了sigmoid函数的非0均值问题和ReLU函数的Dead ReLU问题。

简而言之，只有线性的模型表达能力不够，不能拟合非线性函数，激活函数(Activation Function)是非线性的，只要给予网络足够的隐藏单元，线性+激活函数可以无限逼近任意函数(万能近似定理)。

万能近似定理：Hornik et al. 1989; Cybenko, 1989

加与不加的区别：
线性函数 $f(x)= Wx+b$ 之后添加激活函数 $g(a)$ ，变成
$a(x)=g(f(x))=g(Wx+b)$

神经网络一般都是多层的，所以拿出前三层(包括输入层)来看：有
$a_2(x) = g_2(f_2(g_1(f_1(x)))$

而如果不加激活函数，这三层是这样的：
$y(x)=f_2(f_1(x))$

将f(x)带入上一个表达式：
$y(x)=f_2(f_1(x))=W_2(W_1x+b_1)+b_2=W_2W_1x+(W_2b_1+b_2)$

可以看出来网络还是线性的，还是没有拟合非线性函数的能力，而且不管网络有几层都还是相当于单层线性网络。

非线性：这是必须的，也是添加激活函数的原因。
几乎处处可微：反向传播中，损失函数要对参数求偏导，如果激活函数不可微，那就无法使用梯度下降方法更新参数了。(ReLU只在零点不可微，但是梯度下降几乎不可能收敛到梯度为0)
计算简单：神经元(units)越多，激活函数计算的次数就越多，复杂的激活函数会降低训练速度。
非饱和性：饱和指在某些区间梯度接近于零，使参数无法更新。Sigmoid和tanh都有这个问题，而ReLU就没有，所以普遍效果更好。
有限的值域：这样可以使网络更稳定，即使有很大的输入，激活函数的输出也不会太大。

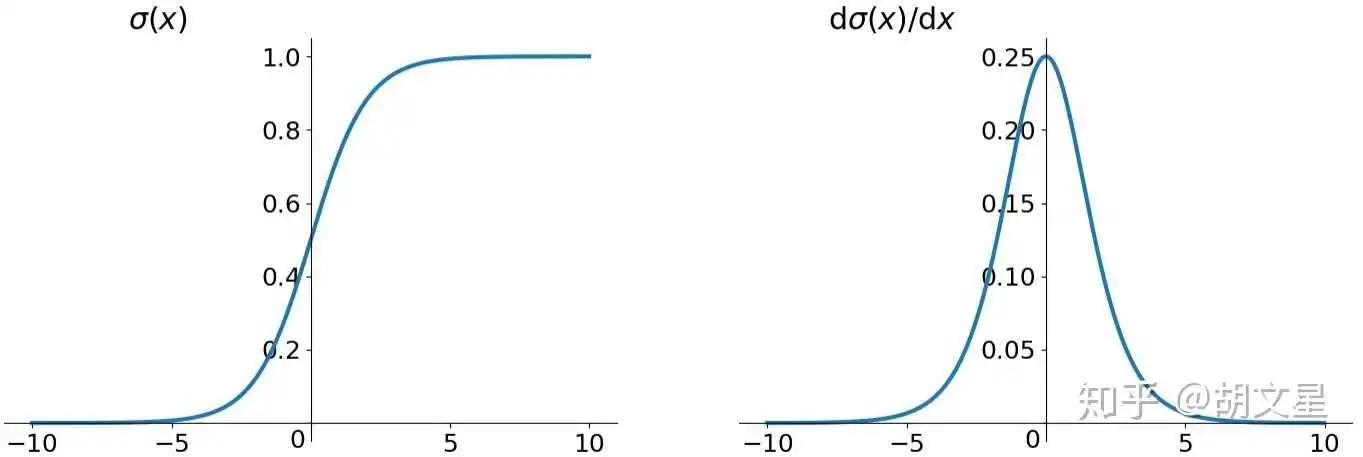
Sigmoid函数公式：
$f(x)=\frac{1}{1+e^{-x}}$

1. Sigmoid容易饱和

输入太大或太小都会使其梯度接近0，这点从图像就能看出来，在反向传播中梯度接近0时参数就会难以更新。另外还需要将参数初始化得比较小才能避免刚开始就梯度为0。

2. Sigmoid的输出不是0均值的

比如激活函数：(式中xx是上层神经元的输出，也是这层神经元的输入)

$f(x,w,b)=f(\sum w_ix_i+b)$

训练过程中通过反向传播学习参数，即通过链式法则，求损失函数 $L(x)$ 对某一参数 $w_i$ 的偏导数(梯度)，通过以下式子更新参数 $w_i$ ：(其中 $\eta$ 是学习率)

$w_i \gets w_i - \eta\cdot\frac{\partial L}{\partial w_i}$

$L(x)$ 对 $w_i$ 求偏导：

$\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial f}\frac{\partial f}{\partial w_i}=\frac{\partial L}{\partial f}\cdot x_i\cdot f(1-f)$

参数更新方向：
因为此处的 $f$ 是simgoid函数，值域为(0, 1)，所以 $f(1-f)$ 恒大于0，又因为 $\frac{\partial L}{\partial f}$ 对所有 $w_i$ 是常数，所以 $w_i$ 更新的方向完全由 $x_i$ 的符号决定， $x_i$ 是上层Sigmoid激活函数的输出，即 $x_i>0$ ，所有 $x_i$ 的符号是一样的，所以所有参数 $w_i$ 的更新方向只能一致。
举个例子：如果向最优解优化，参数 $w_1$ 需要变小，而 $w_2$ 需要变大，而每次梯度下降 $w_1$ 和 $w_2$ 只能向一个方向更新，只能一起变大或一起变小，这样模型收敛就需要消耗很多的时间。
而如果所有 $x_i$ 是零均值的，有正有负的，就不会出现上面的问题了。

3.幂运算相对比较耗时：这个不算太大的问题

函数公式：
$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

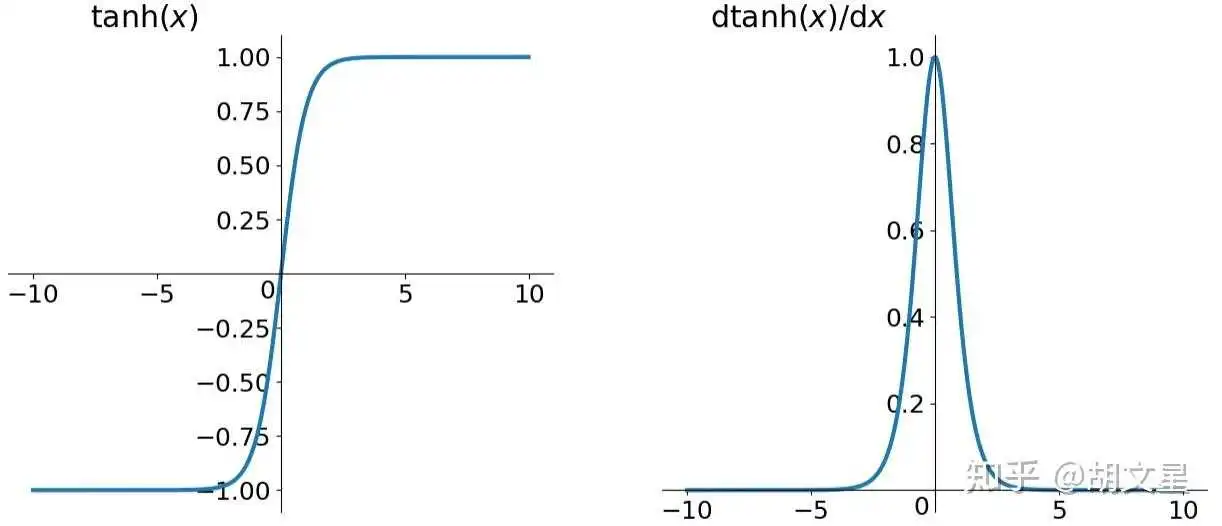
tanh激活函数的性质几乎和Sigmoid一样，主要解决了Sigmoid的输出非0均值问题，模型收敛更快，但还是存在梯度消失的问题。另外Sigmoid的这个输出0~1的性质可以使它的输出作为概率使用。

ReLU，线性整流函数(Rectified Linear Unit)，又称修正线性单元。
函数公式：
$f(x)=max(0,x)$

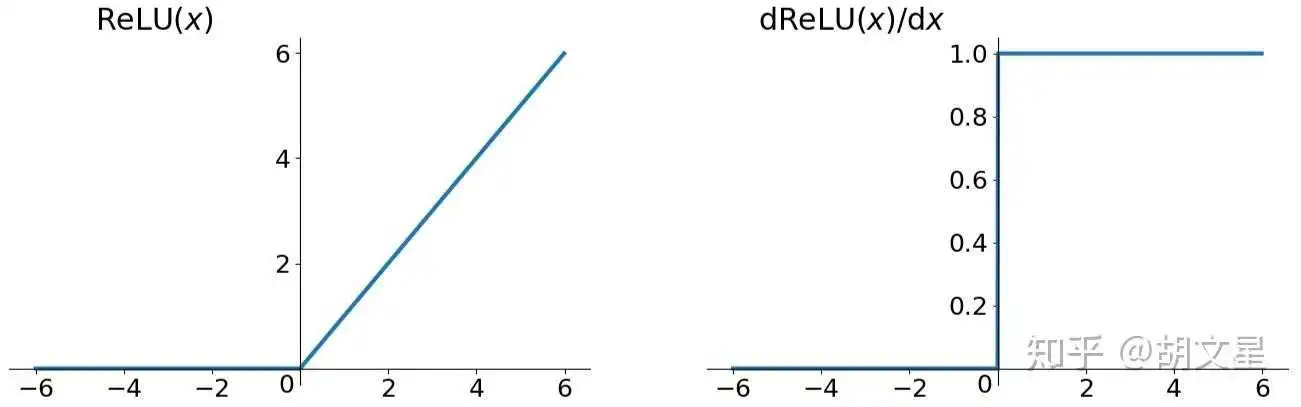
Relu是近几年最常用且很有效的激活函数，虽然也有缺陷但还是推荐优先使用。

优点：
1.解决了梯度消失问题(正区间)
2.计算速度快，只需要判断正负
3.收敛速度比Sigmoid和tanh快很多
缺点：
1.输出不是0均值的
2.Dead ReLU Problem：一些神经元可能永远不能被激活，导致相应参数不能更新。下面分析一下这个问题的原因：

首先我们把 $w$ 参数的更新公式写出来：式中 $\eta$ 是学习率
$w_i \gets w_i - \eta\cdot\frac{\partial L}{\partial w_i}$

损失函数对 $w_i$ 求导(激活函数为ReLU)：式中 $x_i$ 是上层神经元的输出(上层激活函数的输出)
$\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial f}\frac{\partial f}{\partial w_i}=\frac{\partial L}{\partial f}\cdot x_i$

将两个式子合并：
$w_i \gets w_i - \eta\cdot \frac{\partial L}{\partial f}\cdot x_i$

因为 $x_i$ 是上层各个神经元的输出，即上层每个神经元的激活函数的输出，可知其值一定为0或者正数，为方便说明现在假设 $x_i$ 都为正数。看上式，现在 $x_i$ 为正数，学习率 $\eta$ 肯定也是正数，若损失函数对激活函数的导数 $\frac{\partial L}{\partial f}$ 也是正数且足够大，并假设学习率 $\eta$ 也不小，那么很多 $w_i$ 更新这一次后就变成了负数，这会造成什么影响呢？看该层网络的下次前向传播公式：
$a=f(x,w,b)=ReLU(\sum w_ix_i+b)$

其中 $a$ 是这个神经元的输出，下层网络的输入。由上面假设，所有 $x_i$ 都为正数，多数 $w_i$ 为负数，那么： $\sum w_ix_i+b$ 很大概率是个负数，由ReLU图像可知，输入为负数，输出就为0，即 $a=ReLU(负数)=0$ 。

由前向传播公式可以看出，若神经元的输出为0，那么该神经元的前向传播在该层与下层网络之间就断开了，从而反向传播也就断了。

造成Dead ReLU Problem问题的主要原因可能为：
1.学习率 $\eta$ 太大导致参数更新幅度太大
2.糟糕的权重初始化

为了解决成Dead ReLU Problem问题，又有了Leaky ReLU函数和ELU (Exponential Linear Units) 函数。

函数公式：
$f(x)=max(0.01x,x)$

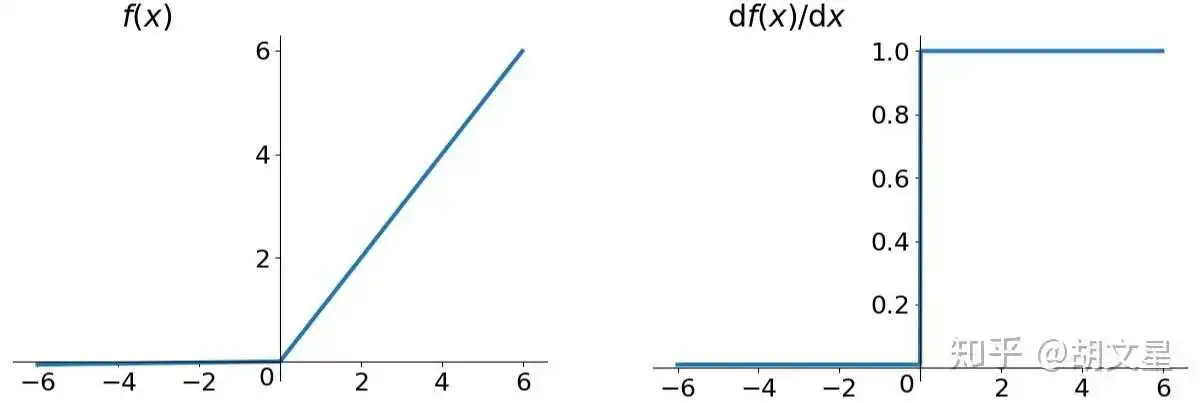
前半段是0.01x而不是0，解决了Dead ReLU Problem问题。
还有一种想法是通过反向传播训练这个前半段函数： $f(x)=max(\alpha x,x)$ ，其中 $\alpha$ 可以训练。
虽然这两种函数理论上比ReLU好，但是实践中并没有完全证明优于ReLU。

ELU (Exponential Linear Units)

函数公式：
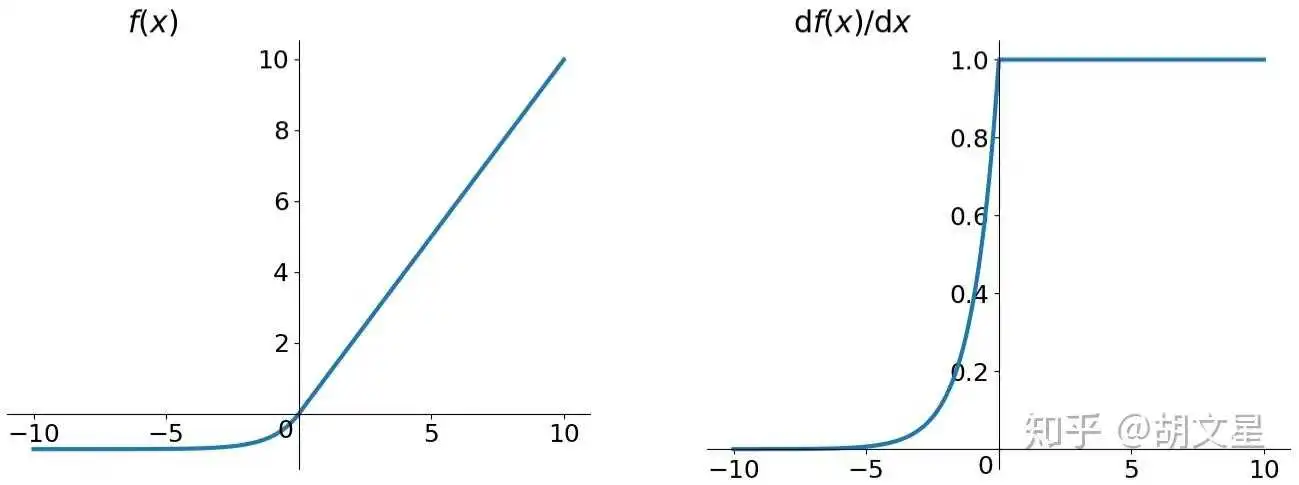
$f(x)=\begin{cases} x,\;\;\;\;\;\;\;\;\;\;\;\;\; x>0 \\ \alpha (e^x-1), x<=0\end{cases}$

虽然也解决了Dead ReLU Problem，并且输出接近0均值，但是也没有在实践中完全证明优于ReLU。

Sigmoid可以当作二分类概率输出使用，但不建议当作中层激活函数。推荐使用ReLU，需要注意学习率的设置，ReLU变种可以尝试。

[1] Deep Learning 花书
[2] 神经网络中激活函数的真正意义？一个激活函数需要具有哪些必要的属性？还有哪些属性是好的属性但不必要的？
[3]【机器学习】神经网络-激活函数-面面观(Activation Function)
[4] 谈谈激活函数以零为中心的问题
[5] 聊一聊深度学习的activation function
[6] ‘Dead ReLU Problem’ 产生的原因

1.什么是激活函数？

所谓激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如图，在神经元中，输入（inputs ）通过加权，求和后，还被作用在一个函数上，这个函数就是激活函数。

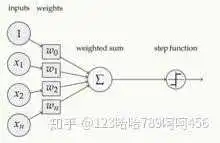
2.为什么要用激活函数？

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

3.激活函数为什么是非线性的？

如果使用线性激活函数，那么输入跟输出之间的关系为线性的，无论神经网络有多少层都是线性组合。

使用非线性激活函数是为了增加神经网络模型的非线性因素，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。

输出层可能会使用线性激活函数，但在隐含层都使用非线性激活函数。

4.常用的激活函数：sigmoid，Tanh，ReLU，Leaky ReLU，PReLU，ELU，Maxout

(1) sigmoid函数

sigmoid函数又称 Logistic函数，用于隐层神经元输出，取值范围为(0,1)，可以用来做二分类。

sigmoid函数表达式： $\sigma(x)=\frac{1}{1+e^{-x}}$

它的导数为：

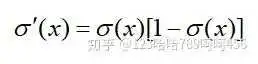
sigmoid函数的几何形状是一条S型曲线，图像如下：

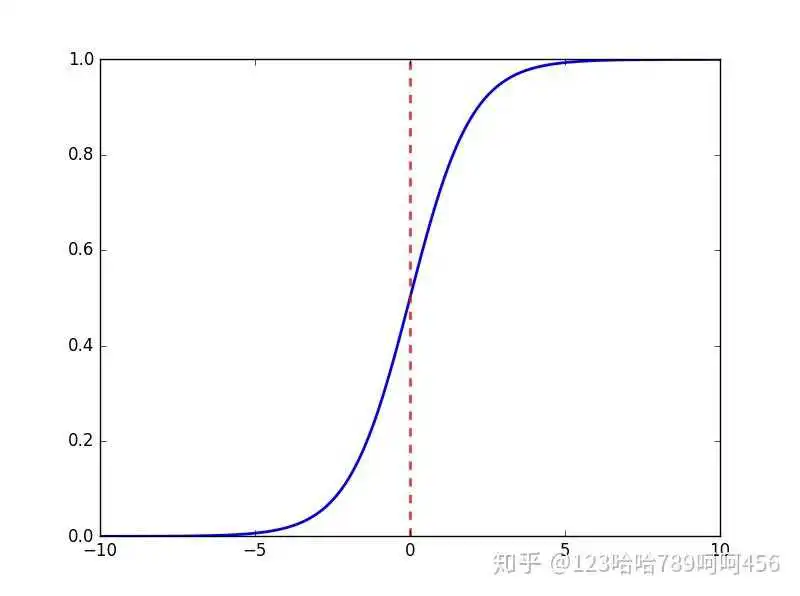
优点：

Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
连续函数，便于求导。

缺点：

1. sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象，意味着函数会变得很平，并且对输入的微小改变会变得不敏感。

在反向传播时，当梯度接近于0，权重基本不会更新，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

2. sigmoid函数的输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。

3. 计算复杂度高，因为sigmoid函数是指数形式。

(2) Tanh函数

Tanh函数也称为双曲正切函数，取值范围为[-1,1]。

Tanh函数定义如下：

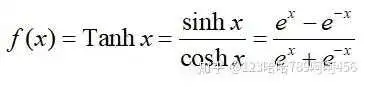
它的导数为：

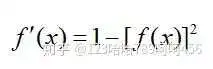
函数图像如下：

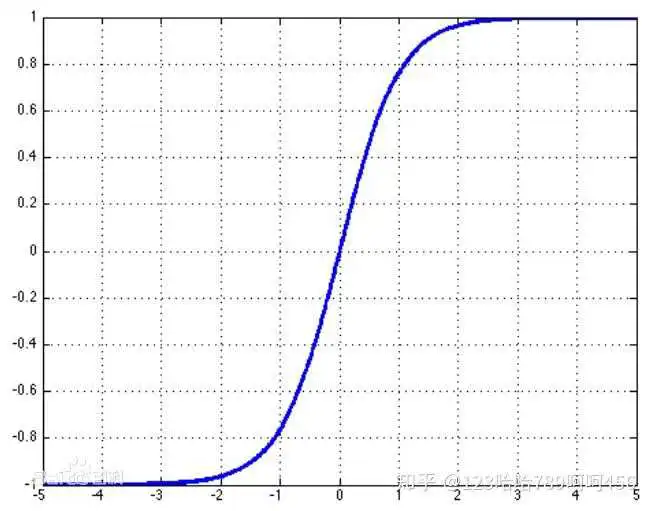
Tanh函数是 sigmoid 的变形：

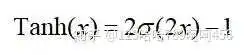
Tanh函数是 0 均值的，因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题。

(3) ReLU函数

整流线性单元（Rectified linear unit，ReLU）是现代神经网络中最常用的激活函数，大多数前馈神经网络默认使用的激活函数。

ReLU函数定义如下： $f(x)=max(0,x)$

函数图像如下：

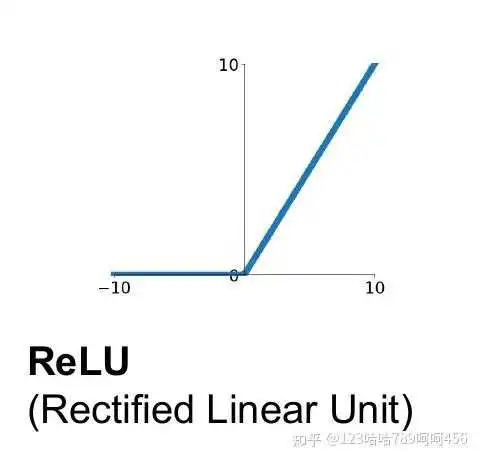
优点：

使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。

2. 在x>0区域上，不会出现梯度饱和、梯度消失的问题。

3. 计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。

缺点：

ReLU的输出不是0均值的。

2. Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。

产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

(4) Leaky ReLU函数

渗漏整流线性单元(Leaky ReLU)，为了解决dead ReLU现象。用一个类似0.01的小值来初始化神经元，从而使得ReLU在负数区域更偏向于激活而不是死掉。这里的斜率都是确定的。

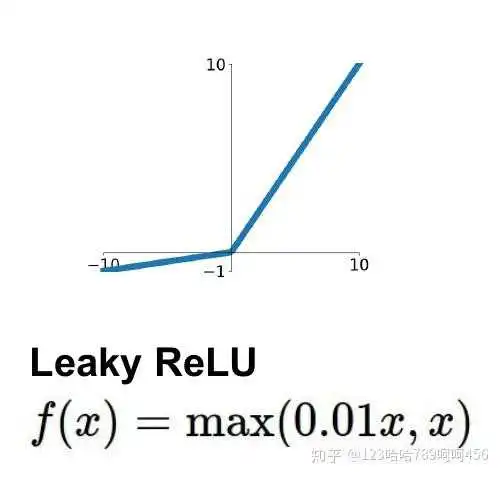
(5) PReLU

参数整流线性单元(Parametric Rectified linear unit，PReLU)，用来解决ReLU带来的神经元坏死的问题。

公式： $f(x)=max(\alpha x,x)$ 。其中 $\alpha$ 不是固定的，是通过反向传播学习出来的。

(6) ELU

指数线性单元(ELU)：具有relu的优势，没有Dead ReLU问题，输出均值接近0，实际上PReLU和Leaky ReLU都有这一优点。有负数饱和区域，从而对噪声有一些鲁棒性。可以看做是介于ReLU和Leaky ReLU之间的一个函数。当然，这个函数也需要计算exp，从而计算量上更大一些。

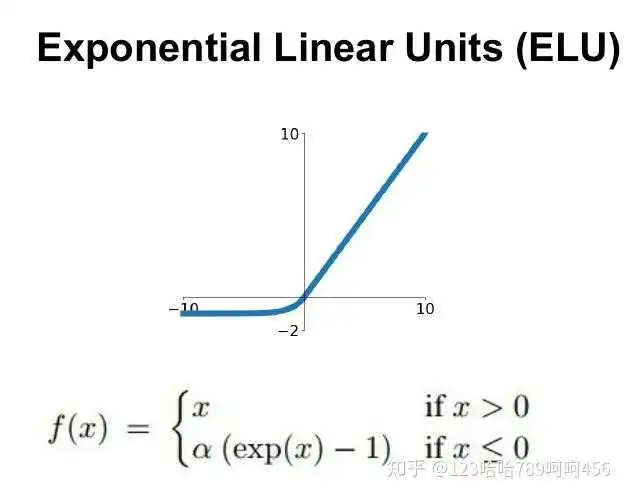
(7) Maxout

论文链接：https://arxiv.org/pdf/1302.4389.pdf

推荐一篇博客，讲的很好：https://blog.csdn.net/hjimce/article/details/

Maxout隐藏层每个神经元的计算公式如下：

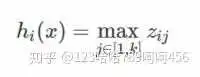
其中 k 是Maxout层的参数。权重 W 是一个大小为(d,m,k)三维矩阵，b是一个大小为(m,k)的二维矩阵，这两个就是我们需要学习的参数。

Maxout是通过分段线性函数来拟合所有可能的凸函数来作为激活函数的，但是由于线性函数是可学习，所以实际上是可以学出来的激活函数。具体操作是对所有线性取最大，也就是把若干直线的交点作为分段的边界，然后每一段取最大。

优点：

Maxout的拟合能力非常强，可以拟合任意的凸函数。

2. Maxout具有ReLU的所有优点，线性、不饱和性。

3. 不会出现神经元坏死的现象。

缺点：增加了参数量。

一提起Sigmoid function可能大家的第一反应就是Logistic Regression。我们把一个sample扔进 $sigmoid$ 中，就可以输出一个probability，也就是是这个sample属于第一类或第二类的概率。

还有像神经网络也有用到 $sigmoid$ ，不过在那里叫activation function。

Sigmoid function长下面这个样子：
$\sigma(z) = \dfrac{1}{1+e^{-z}}\\$

其实这个function我们只知道怎么用它，但是不知道它是怎么来的，以及底层的含义是什么。知乎有人解答不过都是照着教材抄一抄捞几个赞，那么我详细的解释一下，争取不要让算法工程师沦为调参工程师。

首先假设我们有两个class： $C_{1}$ 和 $C_{2}$ ，并且给出一个sample $x$ ，我们的目标是求 $x$ 属于 $C_{1}$ 的概率是多少。

这个概率我们可以通过Naive Bayes很轻松的得出，也就是（公式1）：

$P(C_{1} | x) = \dfrac{P(x|C_{1})P(C_{1})}{P(x)}\\$

其中等号右面的分布这项（公式2）：

$P(x) = P(x | C_{1})P(C_{1}) + P(x | C_{2})P(C_{2})\\$
这个公式是高中难度的，不过也解释一下： $x$ 出现的概率等于， $C_{1}$ 出现的概率乘以 $C_{1}$ 中出现 $x$ 的概率加上 $C_{2}$ 出现的概率乘以 $C_{2}$ 中出现 $x$ 的概率。

那么就可以把公式2带入公式1的分母中（公式3）：

$P(C_{1} | x) = \dfrac{ P(x|C_{1})P(C_{1}) }{P(x|C_{1})P(C_{1})+P(x|C_{2})P(C_{2})}\\$

下面我们将等式两边同时除以分子就变成了（公式4）：

$P(C_{1} | x) = \dfrac{1}{1+ \dfrac{P(x|C_{2})P(C_{2})}{P(x|C_{1})P(C_{1})}}\\$

设 $z = \ln\dfrac{P(x|C_{1})P(C_{1})}{P(x|C_{2})P(C_{2})}$

那么把 $z$ 带入公式4就变成了：

$\sigma(z) = \dfrac{1}{1+e^{-z}}\\$
也就是Sigmoid function

上面已经知道 $sigmoid$ 函数是从什么东西推导过来的了，那么有个问题就是，既然上面式子中只有 $P(x|C_{1})$ 和 $P(x|C_{2})$ 我们不知道，那我们干脆用Bayes不就能直接计算出 $P(x|C_{1})$ 了嘛？
（x是某个sample，其中有多个feature，也就是说x是一个vector）

$P(x|C_{1}) = P(x_{1}|C_{1})P(x_{2}|C_{1})......P(x_{k}|C_{1})...... \\$

但是Bayes有一个限制条件就是所有的feature都必须是independent的，假如我们训练的sample中各个feature都是independent的话，那么Bayes会给我们一个很好的结果。但实际情况下这是不太可能的，各个feature之间不可能是independent的，那么bias就会非常大，搞出的model就很烂。

我们将 $z$ 变换一下可以变换成下面的样子：

$z = \ln\dfrac{P(x|C_{1})}{P(x|C_{2})} + \ln\dfrac{P(C_{1})}{P(C_{2})}\\$

上式中 $\ln\dfrac{P(C_{1})}{P(C_{2})}$ 中的 $\dfrac{P(C_{1})}{P(C_{2})}$ 是很好求的，设 $C_{1}$ 在训练集中出现的数目是 $N_{1}$ ， $C_{2}$ 在训练集中出现的数目是 $N_{2}$ ，那么：

$\ln\dfrac{P(C_{1})}{P(C_{2})} = \ln\dfrac{\dfrac{N_{1}}{N_{1}+N_{2}}} {\dfrac{N_{2}}{N_{1}+N_{2}}} = \ln\dfrac{N_{1}}{N_{2}}\\$

其中 $P(x|C_{1})$ 和 $P(x|C_{2})$ 都遵从Guassian probability distribution：

$P(x|C_{1}) = \dfrac{1}{2\pi^{D/2}} \dfrac{1}{\left | \Sigma_{1} \right |^{1/2}} e^{-1/2(x-\mu_{1})^T\Sigma_{1}^{-1}(x-\mu_{1})}\\$
$P(x|C_{2}) = \dfrac{1}{2\pi^{D/2}} \dfrac{1}{\left | \Sigma_{2} \right |^{1/2}} e^{-1/2(x-\mu_{2})^T\Sigma_{2}^{-1}(x-\mu_{2})}\\$

那么我们再回到这个公式中：

$z = \ln\dfrac{P(x|C_{1})}{P(x|C_{2})} + \ln\dfrac{P(C_{1})}{P(C_{2})}\\$

第二项我们已经求出来了，下面我们把第一项Guassian probability distribution带入：

$\ln\dfrac{P(x|C_{1})}{P(x|C_{2})} = \ln\dfrac {\dfrac{1}{2\pi^{D/2}} \dfrac{1}{\left | \Sigma_{1} \right |^{1/2}} e^{-1/2(x-\mu_{1})^T\Sigma_{1}^{-1}(x-\mu_{1})}} {\dfrac{1}{2\pi^{D/2}} \dfrac{1}{\left | \Sigma_{2} \right |^{1/2}} e^{-1/2(x-\mu_{2})^T\Sigma_{2}^{-1}(x-\mu_{2})}}\\$

乍一看，我滴妈简直太复杂太恶心了 :)
但是别慌，很多东西都能消掉的，我们来消一下。
首先，上面分子分母中 $\dfrac{P(x|C_{1})}{P(x|C_{2})}$ 可以消掉，就变成了：

$\ln\dfrac{P(x|C_{1})}{P(x|C_{2})} = \ln\dfrac {\dfrac{1}{\left | \Sigma_{1} \right |^{1/2}} e^{-1/2(x-\mu_{1})^T\Sigma_{1}^{-1}(x-\mu_{1})}} {\dfrac{1}{\left | \Sigma_{2} \right |^{1/2}} e^{-1/2(x-\mu_{2})^T\Sigma_{2}^{-1}(x-\mu_{2})}}\\$

接着拆：

$\ln\dfrac{P(x|C_{1})}{P(x|C_{2})} = \ln\dfrac{\left | \Sigma_{2} \right |^{1/2}} {\left | \Sigma_{1} \right |^{1/2}} e^{-1/2[(x-\mu_{1})^{T}(\Sigma_{1})^{-1}(x-\mu_{1})-(x-\mu_{2})^{T}(\Sigma_{2})^{-1}(x-\mu_{2})]}\\$

再拆：
$\ln\dfrac{P(x|C_{1})}{P(x|C_{2})} = \ln\dfrac{\left | \Sigma_{2} \right |^{1/2}} {\left | \Sigma_{1} \right |^{1/2}} - \dfrac{1}{2}[(x-\mu_{1})^{T}(\Sigma_{1})^{-1}(x-\mu_{1})-(x-\mu_{2})^{T}(\Sigma_{2})^{-1}(x-\mu_{2})]\\$

上式中第二项 $\dfrac{1}{2}[(x-\mu_{1})^{T}(\Sigma_{1})^{-1}(x-\mu_{1})-(x-\mu_{2})^{T}(\Sigma_{2})^{-1}(x-\mu_{2})]$ ，中括号里面有两项，我再把这两项里面的括号全都打开，打开的目的是为了后面的化简，首先先看第一项：
$(x-\mu_{1})^{T}(\Sigma_{1})^{-1}(x-\mu_{1})-(x-\mu_{2})^{T}(\Sigma_{2})^{-1}(x-\mu_{2}) = x^{T}\Sigma_{1}^{-1}x - x^{T}\Sigma_{1}^{-1}\mu_{1} - \mu_{1}^{T}\Sigma_{1}^{-1}x + \mu_{1}^{T}\Sigma^{-1}\mu_{1}\\$

$= x^{T}\Sigma_{1}^{-1}x - 2\mu_{1}^{T}\Sigma_{1}^{-1}x + \mu_{1}^{T}\Sigma_{1}^{-1}\mu_{1}\\$

第二项化简方法一样，把下角标换成2就行了：

$(x-\mu_{2})^{T}(\Sigma_{2})^{-1}(x-\mu_{2}) = x^{T}\Sigma_{2}^{-1}x - 2\mu_{2}^{T}\Sigma_{2}^{-1}x + \mu_{2}^{T}\Sigma_{2}^{-1}\mu_{2}\\$

拆的差不多了，下面我们回到 $z = \ln\dfrac{P(x|C_{1})}{P(x|C_{2})} + \ln\dfrac{P(C_{1})}{P(C_{2})}$ 中，把刚才的化简结果带进去：
$z = \ln\dfrac{\left | \Sigma_{2} \right |^{1/2}} {\left | \Sigma_{1} \right |^{1/2}} - \dfrac{1}{2}[x^{T}\Sigma_{1}^{-1}x - 2\mu_{1}^{T}\Sigma_{1}^{-1}x + \mu_{1}^{T}\Sigma_{1}^{-1}\mu_{1} - x^{T}\Sigma_{2}^{-1}x + 2\mu_{2}^{T}\Sigma_{2}^{-1}x - \mu_{2}^{T}\Sigma_{2}^{-1}\mu_{2}] + \ln\dfrac{N_{1}}{N_{2}}$

仔细观察不难发现，上式中中括号里面第一项和第四项是可以消掉的。
并且我们可以认为 $\Sigma_{1} = \Sigma_{2} = \Sigma$ ，刚才我一直没解释 $\mu$ 和 $\Sigma$ 是什么，下面我简单说一下， $\mu$ 就是mean（均值）， $\Sigma$ 就是covairance（协方差），其中 $\mu$ 是个vector， $\Sigma$ 是个matrix，具体什么形式不在本文里详细解释，一解释就没完没了了，可以深推一下Guassian看看paper（个人感觉意义不大，其实理解到这里完全够用了）。

好了，为什么可以认为 $\Sigma_{1} = \Sigma_{2} = \Sigma$ 呢？因为如果每个class都有自己的covariance的话，那么variance会很大，参数的量一下就上去了，参数一多，就容易overfitting。这么说的话， $z$ 里面的第一项 $\ln\dfrac{\left | \Sigma_{2} \right |^{1/2}} {\left | \Sigma_{1} \right |^{1/2}}$ 就是0了。

好开心，又有好多东西被约掉了 :)

最后， $z$ 被化简成了下面这种最终形态：

$z = (\mu_{1}-\mu_{2})\Sigma^{-1}x - \dfrac{1}{2}\mu_{1}^{T}\Sigma^{-1}\mu_{1} + \dfrac{1}{2}\mu_{2}^{T}\Sigma^{-1}\mu_{2} + \ln\dfrac{N_{1}}{N_{2}}\\$

可以观察到，第一项有系数 $x$ ，后面几项里其实都是参数。
我们就可以理解为x的系数其实就是 $sigmoid$ 中的参数 $w^{T}$ （这是个matrix），后面那些项可以看成是参数 $b$ 。

那么在Generative model中我们的目标是寻找最佳的 $N_{1},N_{2},\mu_{1},\mu_{2},\Sigma$ 使 $P(C_{1}|x)$ maximise。

但是我们已经将一连串复杂的参数和方程化简成了 $z = \sigma(w^{T}x + b)$ 那为什么还要舍近求远的求5个参数去将目标最优化呢？只有“两个参数”的方法我们叫做Discraminative model。

实际上，在大多数情况下，这两种方法各有利弊，但是实际上Discraminative model泛化能力比Generative model还是强不少的。什么时候Generative model更好呢？

- training data比较少的时候，需要靠几率模型脑补没有发生或的事情。
- training data中有noise。

整个 $sigmoid$ 的推导到这里就结束了，欢迎交流！

本文地址：

softmax与sigmoid函数的理解__的博客-CSDN博客

在使用逻辑回归做二分类问题时，sigmoid函数常用作逻辑回顾的假设函数，从直觉上理解很好理解，就是在线性回归的基础上套一个sigmoid函数，将线性回归的结果 $(-\infty,+\infty )$ ，映射到 $(0,1)$ 范围内，使他变为一个二分类问题。但是在sigmoid背后有一套严谨的数学推导，包括sigmoid函数时怎么推导出来的，为什么使用sigmoid函数。

逻辑回归和线性回归同属一个广义线性模型，顾名思义，这些模型有相似之处，实在同一套约束下设计出来的。例如解决一个二分类问题，首先假设这个问题可以使用广义线性模型来解决，其次假设数据的概率分布情况，发现是二分类问题，假设数据服从伯努利分布，然后使用MLE计算最优化的概率，从而学习参数的值。具体可以参考我写的这篇：

广义线性模型总结（GLM）__的博客-CSDN博客_glm广义线性模型应用场景

广义线性模型有一些性质，这些模型的数据分布同属指数分布族，概率密度函数的通式如下：

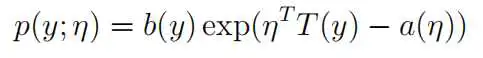
其中：

$\eta$ ：分布的自然参数（natural parameter）或标准参数（canonical parameter）
$T(y)$ ：充分统计量（sufficient statistic），一般等于y
$a(\eta)$ ：对数分配函数（log partition function），这部分确保Y的分布p(y:η) 计算的结果加起来（连续函数是积分）等于1。
$b(y)$ ：基础度量值（base measure）

将伯努利分布的概率密度函数套入这个指数分布族的概率密度函数中，可以一一对应的找到 $\eta, T(y), a(\eta), b(y)$ 四个值。伯努利分布是特殊的二项分布，概率密度函数可以写为：

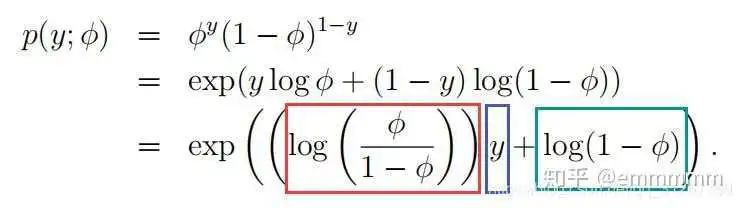
其中标出的分别是：

$\eta=log(\frac{\phi }{1-\phi })$ ，反解出： $\phi =\frac{1}{1+e^{-\eta}}$

$T(y)=y$

把 $\phi$ 带入 $a(\eta)$ 可以求解出：

$a(\eta)=-log(1-\phi)=log(1+e^{\eta})$

$b(y)=1$

逻辑回归其实就是使用伯努利分布对目标数据进行无偏估计，无偏估计的定义是这样的：估计量的数学期望等于被估计参数的真实值，则称此估计量为被估计参数的无偏估计，即具有无偏性，是一种用于评价估计量优良性的准则。即：要使用估计量的数学期望去估计真实值。

而对于指数分布族其中一个重要的性质就是：概率分布的数学期望是对数分配函数（log partition function） $a(\eta)$ 的一阶偏导： $E[y|x]=\frac{\partial}{\partial \eta}a(\eta)$ ，这样可以很轻易求出来我们的估计量，把 $\phi$ 带入 $a(\eta)$ 并对 $a(\eta)$ 求偏导： $E[y|\eta]=a'(\eta)=\frac{e^{\eta}}{1+e^{\eta}}=\frac{1}{1+e^{-\eta}}$

可以发现，这就是sigmoid函数，利用广义线性模型的另一条假设：自然参数 $\eta$ 和 $x$ 满足线性关系： $\eta=\theta^{T}x$ ，也就可以推导出逻辑回归的假设函数：

$h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T}x}}$

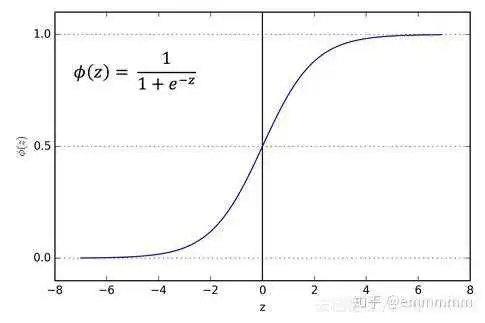
作用：从图片上可以看到，sigmoid是非线性的，所可以用在神经网络中间层中作为激活函数，也可以用在最后一层将结果映射到(0, 1)之间。

优点：

可以看到sigmoid函数处处连续，便于求导；
可以将函数值的范围压缩到[0,1]，可以压缩数据，且幅度不变。
可以做二分类问题；

缺点：

在输入很大的情况下，函数进入饱和区，函数值变化很小，使x对y的区分度不高，同时也容易梯度消失，不利于深层神经网络的反馈传输，反向传输时计算量大。
函数均值不为0，当输出大于0时，则梯度方向将大于0，也就是说接下来的反向运算中将会持续正向更新；同理，当输出小于0时，接下来的方向运算将持续负向更新。

softmax的推导过程与sigmoid很像，sigmoid对应伯努利分布，softmax对应类别分布（categorical distribution），同样可以用上面指数族分布的那种方法推导。

$S_i=\frac{e^i}{\sum_j{e^j}}$

上面是softmax的表达式，softmax用于多分类问题，在多分类神经网络种，常常作为最后一层的激活函数，前一层的数值映射为(0,1)的概率分布，且各个类别的概率归一，从表达式中很容易看出来。与sigmoid不同的是，softmax没有函数图像，它不是通过固定的 $y=f(x)$ 的映射将固定的值映射为固定的值，softmax是计算各个类别占全部的比例，可以理解为输入一个向量，然后出一个向量，输出的向量的个位置的元素表示原向量对应位置的元素所占整个向量全部元素的比例。

很容易想到，原始向量经过softmax之后，原始向量中较大的元素，在输出的向量中，对应位置上还是较大，反之，原始向量中较小的元素还是会很小，保留了原始向量元素之间的大小关系。在做多分类问题时，输出向量的第几维最大，就表示属于第几个class的概率最大，由此分类。

公式中可以看到没有直接将元素求和然后计算比值，而是对每个元素都套了一个exp函数在求和，exp函数是为了将所有值映射为正实数，避免出现概率为负的情况。而使用exp却不适用绝对值的原因，个人认为是为了将较大的元素映射为更大的值，较小的元素映射为更小的值，这样可以更明显的突出较大元素。

在使用word2vec等模型之前提出了使用one-hot向量来描述单词，即设定一个大小为 $V$ 的词库，然后使用一个维数大小为 $V$ 的one-hot向量来描述词库中的所有词，在词库中出现某个词的对应位置，在one-hot向量中那个位置就为1，其余位置为0。

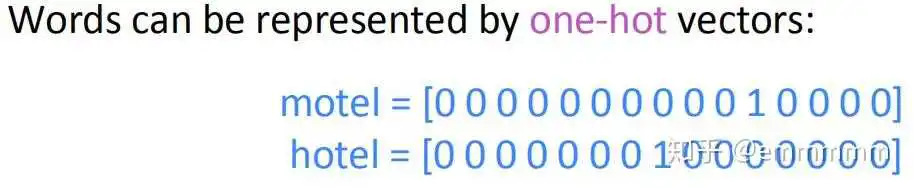
这样在空间中可以表示出了词的位置，便可利用数学手段来计算两个向量之间的关系了，例如计算距离夹角相似度等等，但是这种表示方法却无法表示出词与词，因为每个词独占一维，任意两个不相同的向量点积永远为0。之后便提出了word2vec的一些模型。

这里先忽略模型细节的推导过程，主要说一下对于在模型中使用softmax计算每个词的概率我得理解。首先要解决的问题时onehot向量正交的问题，丢失了词与词之间的关系信息。首先softmax的好处就是经过softmax的向量一定是每一维都不为0的稠密向量，这样向量做点积不会为0，保留了词与词之间的关系。

其次要保留词本身的意思，第二个原因就是原始向量经过softmax之后，原始向量中较大的元素，在输出的向量中，对应位置上还是较大，反之，原始向量中较小的元素还是会很小，保留了原始向量元素之间的大小关系。也就是说，如果将最大的一维表示为1，其余均抹除掉变为0，这样就还原成了onehot向量表示，所以可以直觉的理解，softmax的做法确实保留了onehot表示的信息，但是会有一定信息损失，毕竟onehot的向量维数远大于softmax计算出来的向量，这其实也是另外一个优点，解决了onehot向量维数过大的问题。

在词向量计算中softmax和one-hot应该是相对应的，soft对应的是向量更加稠密，如果说极端情况每一维代表一个词的话，在除了词本身的维度以外的元素值，都表示这个词在其他“词义上的分量”，也就是词与词之间的关系；相比onehot要更加稀疏，更“hard”一些，直接将除了所表示词本身的元素以外的都压成了0，所以丢失了关系信息，而max对应的表示原来最大的元素，现在仍然保留，抽象理解保留了最基本的词义。

在这里想到了sigmoid函数，softmax是用来做多分类的，sigmoid是用来做二分类的，可以理解为sigmoid是softmax当类别数为2的特殊情况，可以看到sigmoid函数的曲线是不断趋近于0或者1，而最终结果是要得到一个0或1的离散值，那为什么不用sign函数代替，除了sign的梯度为0不能反向传播以外，我认为是sigmoid函数比sign更“soft”一点，在不影响结果的情况下，还保留了一些其他的信息，上面sigmoid函数的优点中也提到，可以压缩数据且幅度不变，y保留了x之间的大小关系，不光可以区分属于不同类的元素，还可以区分属于同一类的元素谁更属于这一类。

有错误欢迎评论区指正。

我的csdn博客地址

_的博客_我对算法一无所知_CSDN博客-算法,机器学习算法,历程领域博主

大部分资料对于LR为什么使用Sigmoid的解释是Sigmoid函数能够把原本的函数压缩在0~1之间，适合作为概率，进而可以分类；然而事实很复杂，在本篇文章将要给出两种解释，最后一种解释最为深入。

逻辑回归使用的函数其实是Sigmoid函数中的一种函数，即 $y=\frac{1}{1+e^{-z}}$ ,实际是对数几率函数。Sigmoid函数指的是S型函数，常见的S型函数还有Tanh函数。 $y=\frac{1}{1+e^{-z}}$ 该函数为什么是对数几率函数的原因如下:

如果把y视作样本x为正例的概率，则1-y为反例的概率，几率是指 $\frac{y}{1-y}$ ，x作为正例的相对可能性，即如果几率大于1，则为正例，小于1则为反例。

对数几率，指的是对几率取对数(同时可以把取值范围限制在0~1)，即为对数几率。

然而，LR(逻辑回归)，可以看作是对数几率的回归，即使用线性函数拟合对数几率

使用广义线性模型解释，首先要解释一下指数族分布。广义线性模型包括逻辑回归、线性回归等。

广义线性模型公式:

$y=g^{-1}(w^Tx+b)$

其中函数g(.)单调可微，该函数成为联系函数。

指数族分布

指数族分布，区别于指数分布。在概率统计中，若某概率分布满足下式，我们称之属于指数族分布。

$P\left(y;\eta\right)=b(y)exp\left(\eta^TT(y)-a(\eta)\right)$

其中 $\eta$ 是natural parameter,T(y)是充分统计量(一般情况下 $T(y)=y$ )， $e^{-a{\eta}}$ 是起到归一化的作用。确定了T,a,b我们就可以确定某个参数为 $\eta$ 的指数族分布。

常见的指数族分布有:泊松分布、gamma分布、beta分布、Dirichlet分布、伯努利分布、高斯分布等。

伯努利分布

$P(y;\Phi)=\Phi^y(1-\Phi)^{1-y} \\ =exp\left(ylog(\Phi)+(1-y)log(1-\Phi)\right)\\ =exp\left(ylog(\frac{\Phi}{1-\Phi})+log(1-\Phi)\right)$

高斯分布

$P(y;\mu)=\frac{1}{\sqrt{2*\Pi}}exp(-\frac{1}{2}(y-\mu)^2)\\ =\frac{1}{\sqrt{2\Pi}}exp(-\frac{1}{2}y^2)exp(\mu y-\frac{1}{2}\mu ^2)$

以上公式的推导，可以看出伯努利分布和高斯分布均为指数族分布。

对于二分类问题，我们就是想预测某个随机变量y，y是某些特征x的函数。为了推导出广义线性模型，我们需要做出下面三个假设。

$p(y|x;\Theta)$ 服从指数分布
给了x，我们的目的是为了预测T(y)在给定条件x下的期望。一般情况下T(y)=y，这就意味着我们希望预测 $P(y|x;\Theta)$ =h(x)=E(y|x)
参数和输入x是线性相关的: $\eta=\Theta^Tx$

第3条也体现了线性模型!

对于二分类问题本身是服从伯努利分布，因此本身就是指数族分布， $P(y|x;\Theta)$ ~ $Bernouli(\Phi)$ ，均值为 $\Phi$

$h_{\Theta}(x)=E[y|x;\Theta]\\ =\Phi\\ =\frac{1}{1+e^{-\eta}}\\ =\frac{1}{1+e^{-\Theta^Tx}}$

由指数族分布:

$\eta=log(\frac{\Phi}{1-\Phi})$

以上就是广义线性模型的推导。

以上的两种解释在西瓜书中都有一点点解释，但是没有详细说，本篇文章只是在笔者的能力范围内的书写。

[1].机器学习(西瓜书)

[2].神经网络与深度学习(邱锡鹏)

[3]指数族分布

【机器学习】【白板推导系列】【合集 1～23】_哔哩哔哩 (゜-゜)つロ干杯~-bilibiliAlex：为什么LR要使用sigmod函数

这次聊一个比较偏的问题，是因为这种渐近超越函数方案主要用在FPGA上，在GPU等设备中并没有看到相关的研究和工程落地。目前在FPGA中计算超越函数常用的方法有级数近似法、查表法（LUT）、坐标旋转数字计算（CORDIC）算法和分段线性逼近法。

下面主要以深度学习中比较常用的激活函数sigmoid作为案例：

Sigmoid函数的表达式、导数和其曲线；其有以下特点，平滑易于求导；在x->-inf或者x->inf上，都是饱和区；其取值范围为[0, 1]。

$\sigma(x) = \frac{1}{1+e^{-x}}$

$\sigma(x) ' = \frac{e^{-x}}{1+e^{-x}} = \sigma(x) (1-\sigma(x))$

1：级数法，其泰勒展开公式

$\sigma(x) = \frac{1}{2} + \frac{1}{4}*t-\frac{1}{48}*t^{3} + \frac{1}{480}*t^{5} -\frac{17}{80640}*t^{7} + O(t^{8}) \\$

2：查表法，将函数平均划分成多个等份

3：Piecewise Linear Approximation，每个区间用不同的线性函数去渐近，论文先提到一个这个渐近函数，暂时没找到出处，且论文里面提供公式第二行的x范围应该为 $-8 \le x \lt -1.6$ ，先截图放到这里，后续遇到再来补上出处。

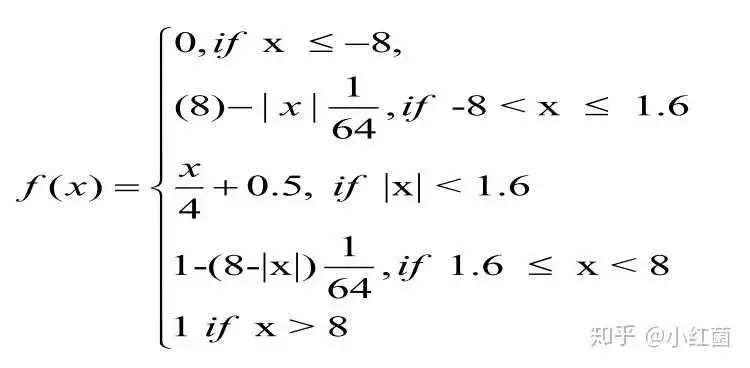
另外Amin根据上述方法，提出一种高效的线性渐近函数，下面的乘法都可以通过移位来实现，所以速度会比普通乘法更快。

$f(x) = \begin{cases} 1, & |x| \ge 5, \\ 0.03125 * |x| + 0.84375, & 2.375 \le |x| \lt 5 \\ 0.125 * |x| + 0.625, & 1 \le |x| \lt 2.375 \\ 0.25 * |x| + 0.5, & 0 \le |x| \lt 1 \\ 1 - f(x), & x < 0 \end{cases} \\$

PWL的方法与sigmoid的曲线误差图如下，可以看出最大一阶误差大于0.015。

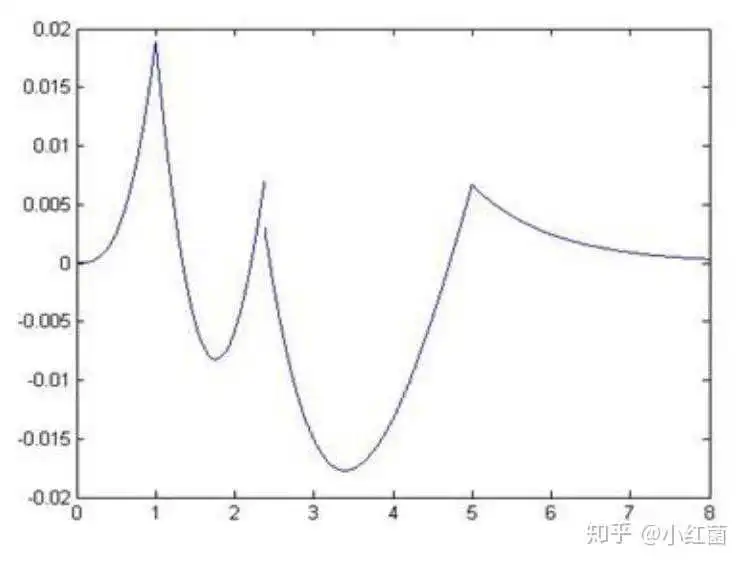
这里提供一个简单的numpy实现，没有利用移位的优势，只是看看来sigmoid函数本身的误差范围。

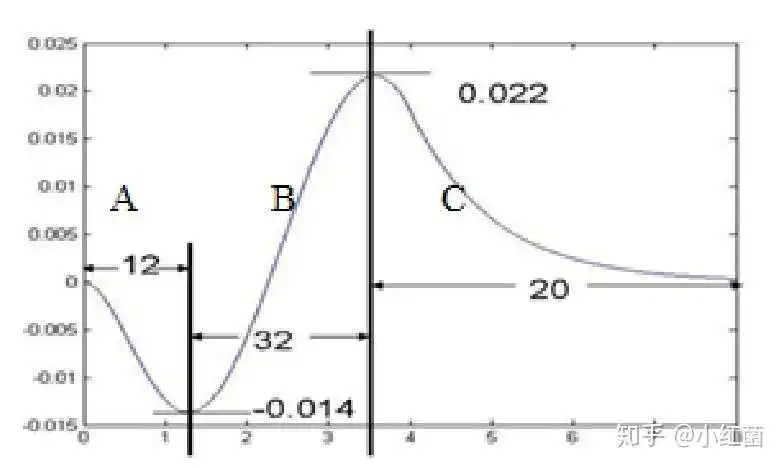
def sigmoid_pwl(x): out = np.zeros_like(x) con1 = np.abs(x) >= 5 out[con1] = 1 con2 = np.logical_and(np.abs(x) < 5, np.abs(x) >= 2.375) out[con2] = 0.03125 * np.abs(x[con2]) + 0.84375 con3 = np.logical_and(np.abs(x) < 2.375, np.abs(x) >= 1) out[con3] = 0.125 * np.abs(x[con3]) + 0.625 con4 = np.logical_and(np.abs(x) < 1, np.abs(x) >= 0) out[con4] = 0.25 * np.abs(x[con4]) + 0.5 con5 = x < 0 out[con5] = 1 - out[con5] return out

4：Piecewise Nonlinear Approximation，前面的方案是通过一次函数进行渐近，还可以通过二次函数。这种方案的缺点在于需要2次乘法和两次加法。Zhang[3]提出的second order nonlinear function(SONF)的函数将将sigmoid分段成4部分，如下公式所示，SONF只需要1次乘法，两个移位和两个异或。

$f(x) = \begin{cases} 1 - \frac{1}{2} (1 - \frac{1}{4}|x|)^{2}, & 0 \lt x \le 4 \\ \frac{1}{2} ( 1 - \frac{1}{4}|x|)^{2}, & -4 \lt x \le 0 \\ 1, & 4 \lt x \\ 0, & x \le -4 \end{cases}\\$

SONF的方法与sigmoid的曲线误差图如下，误差范围在-0.022到0.022之间。

5: CORDIC Function，这种方法是通过使用旋转和移位的操作来实现指数函数。CORDIC可以应用于圆周系统、线性系统和双曲系统等，在不同的系统内解决不同的复杂计算问题。圆周系统中解决三角函数计算问题，线性系统中解决乘法和除法问题。具体可以参考文章[4]。

6: 组合方法，类似于将SONF和LUT方法组合起来，获得效率和精度上的提升。Ngah提出的将SONF和dLUT结合的两步式方法，渐近误差可以缩小到-0.0022 to 0.0022。

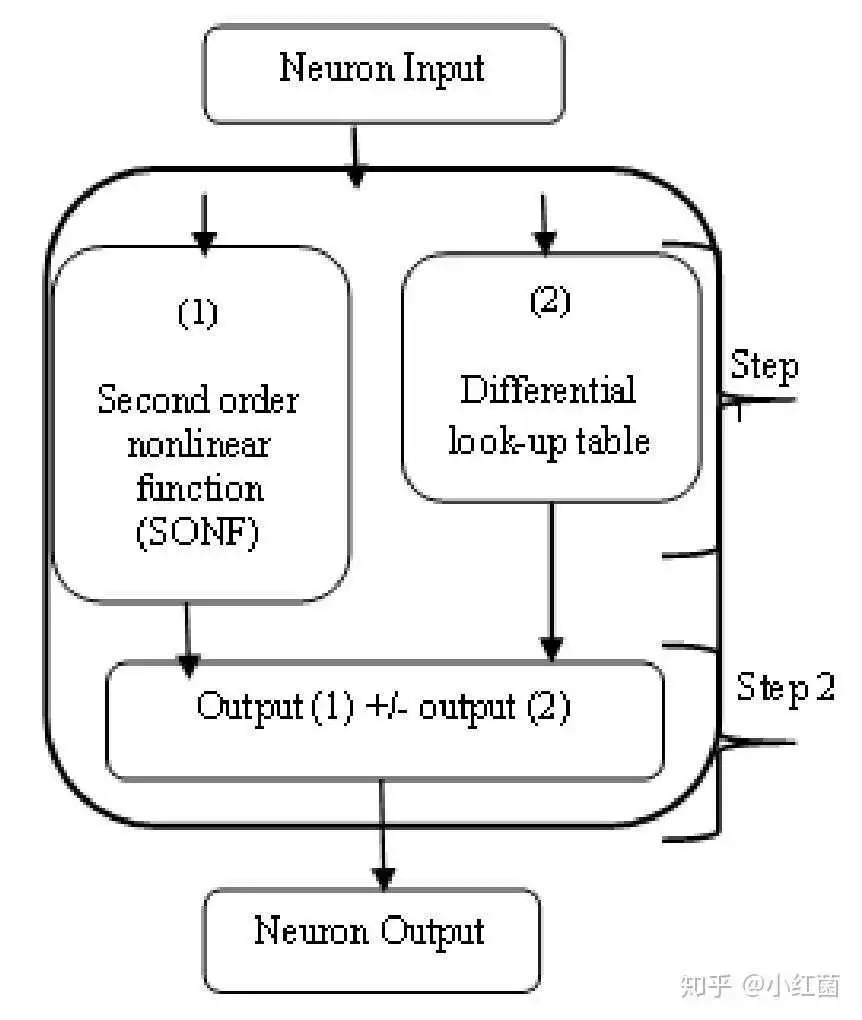
Sigmoid function implementation using the unequal segmentation of differential lookup table and second order nonlinear function
Piecewise linear approximation applied to nonlinear function of a neural network
M. Zhang, S. Vassiliadis, J. G. Delgado-Frias, and S. V. and J. G. D. F. M. Zhang, “Sigmoid generators for neural computing using piecewise approximations,” IEEE Trans. Comput., vol. 45, no. 9, pp. 1045–1049, 1996
FPGA算法学习(1) -- Cordic（圆周系统之旋转模式）

对于Softmax函数和Sigmoid函数，我们分为两部分讲解，第一部分：对于分类任务，第二部分：对于二分类任务（详细讲解）。

Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值。

Sigmoid函数是一种logistic函数，它将任意的值转换到 $[0, 1]$ 之间，如图1所示，函数表达式为： $Sigmoid(x)=\frac{1}{1+e^{-x}}$ 。

它的导函数为： $Sigmoid^{'}(x)=Sigmoid(x)\cdot (1-Sigmoid(x))$ 。

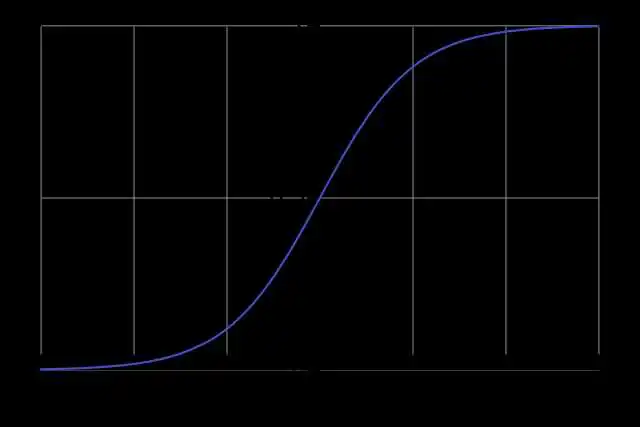
优点：1. Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。2. 连续函数，便于求导。

缺点：1. 最明显的就是饱和性，从上图也不难看出其两侧导数逐渐趋近于0，容易造成梯度消失。2.激活函数的偏移现象。Sigmoid函数的输出值均大于0，使得输出不是0的均值，这会导致后一层的神经元将得到上一层非0均值的信号作为输入，这会对梯度产生影响。 3. 计算复杂度高，因为Sigmoid函数是指数形式。

Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。

Softmax函数，又称归一化指数函数，函数表达式为： $Softmax(x)=\frac{e^{x_{i}}}{\sum_{j=1}^{n}{e^{x_{j}}}}$ 。

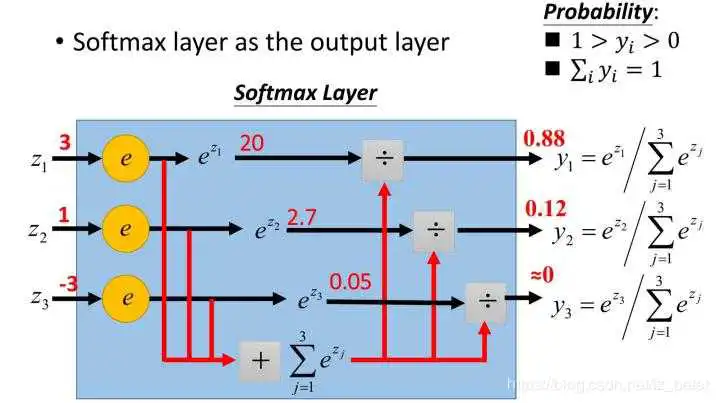
Softmax函数是二分类函数Sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。如图2所示，Softmax直白来说就是将原来输出是3,1,-3通过Softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。

由于Softmax函数先拉大了输入向量元素之间的差异（通过指数函数），然后才归一化为一个概率分布，在应用到分类问题时，它使得各个类别的概率差异比较显著，最大值产生的概率更接近1，这样输出分布的形式更接近真实分布。

Softmax可以由三个不同的角度来解释。从不同角度来看softmax函数，可以对其应用场景有更深刻的理解：

softmax可以当作arg max的一种平滑近似，与arg max操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。
softmax将输入向量归一化映射到一个类别概率分布，即 $n$ 个类别上的概率分布（前文也有提到）。这也是为什么在深度学习中常常将softmax作为MLP的最后一层，并配合以交叉熵损失函数（对分布间差异的一种度量）。
从概率图模型的角度来看，softmax的这种形式可以理解为一个概率无向图上的联合概率。因此你会发现，条件最大熵模型与softmax回归模型实际上是一致的，诸如这样的例子还有很多。由于概率图模型很大程度上借用了一些热力学系统的理论，因此也可以从物理系统的角度赋予softmax一定的内涵。

如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。
如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。
Sigmoid函数可以用来解决多标签问题，Softmax函数用来解决单标签问题。^[1]
对于某个分类场景，当Softmax函数能用时，Sigmoid函数一定可以用。

对于二分类问题来说，理论上，两者是没有任何区别的。由于我们现在用的Pytorch、TensorFlow等框架计算矩阵方式的问题，导致两者在反向传播的过程中还是有区别的。实验结果表明，两者还是存在差异的，对于不同的分类模型，可能Sigmoid函数效果好，也可能是Softmax函数效果。

有对准确率，召回率等不懂的小伙伴可以参考下面的链接：

初识CV：准确率(Precision)、召回率(Recall)、F值(F-Measure)、平均正确率，IoU

首先我们先理论上证明一下二者没有本质上的区别，对于二分类而言（以输入 $x_{1}$ 为例）：

Sigmoid函数： $output(x_{1})=\frac{1}{1+e^{-x_{1}}} (1)$

Softmax函数： $output(x_{1})=\frac{e^{x_{1}}}{e^{x_{1}}+e^{x_{2}}}=\frac{1}{1+e^{-(x_{1}-x_{2})}}(2)$

由公式（2）我们可知， $(x_{1}-x_{2})$ 可以用 $z_{1}$ 代替，即Softmax函数可以写成： $output(z_{1})=\frac{1}{1+e^{-z_{1}}} (3)$ ，和公式（1）完全相同，所以理论上来说两者是没有任何区别的。

然后我们再分析为什么两者之间还存着差异（以Pytorch为例）：

首先我们要明白，当你用Sigmoid函数的时候，你的最后一层全连接层的神经元个数为1，而当你用Softmax函数的时候，你的最后一层全连接层的神经元个数是2。这个很好理解，因为Sigmoid函数只有是目标和不是目标之分，实际上只存在一类目标类，另外一个是背景类。而Softmax函数将目标分类为了二类，所以有两个神经元。这也是导致两者存在差异的主要原因。

Sigmoid函数针对两点分布提出。神经网络的输出经过它的转换，可以将数值压缩到(0,1)之间，得到的结果可以理解成分类成目标类别的概率P，而不分类到该类别的概率是(1 - P)，这也是典型的两点分布的形式。

Softmax函数本身针对多项分布提出，当类别数是2时，它退化为二项分布。而它和Sigmoid函数真正的区别就在——二项分布包含两个分类类别（姑且分别称为A和B），而两点分布其实是针对一个类别的概率分布，其对应的那个类别的分布直接由1-P得出。

简单点理解就是，Sigmoid函数，我们可以当作成它是对一个类别的“建模”，将该类别建模完成，另一个相对的类别就直接通过1减去得到。而softmax函数，是对两个类别建模，同样的，得到两个类别的概率之和是1。

神经网络在做二分类时，使用Softmax还是Sigmoid，做法其实有明显差别。由于Softmax是对两个类别（正反两类，通常定义为0/1的label）建模，所以对于NLP模型而言（比如泛BERT模型），Bert输出层需要通过一个nn.Linear()全连接层压缩至2维，然后接Softmax（Pytorch的做法，就是直接接上torch.nn.CrossEntropyLoss）；而Sigmoid只对一个类别建模（通常就是正确的那个类别），所以Bert输出层需要通过一个nn.Linear()全连接层压缩至1维，然后接Sigmoid（torch就是接torch.nn.BCEWithLogitsLoss）。

总而言之，Sotfmax和Sigmoid确实在二分类的情况下可以化为相同的数学表达形式，但并不意味着二者有一样的含义，而且二者的输入输出都是不同的。Sigmoid得到的结果是“分到正确类别的概率和未分到正确类别的概率”，Softmax得到的是“分到正确类别的概率和分到错误类别的概率”。

一种常见的错法（NLP中）：即错误地将Softmax和Sigmoid混为一谈，再把BERT输出层压缩至2维的情况下，却用Sigmoid对结果进行计算。这样我们得到的结果其意义是什么呢？

假设我们现在BERT输出层经nn.Linear()压缩后，得到一个二维的向量：

[-0.81787, 1.9287]

对应类别分别是(0,1)。我们经过Sigmoid运算得到：

tensor([0.2805, 0.8748])

前者0.2805指的是分类类别为0的概率，0.8748指的是分类类别为1的概率。二者相互独立，可看作两次独立的实验（显然在这里不适用，因为0-1类别之间显然不是相互独立的两次伯努利事件）。所以显而易见的，二者加和并不等于1。

若用softmax进行计算，可得：

tensor([0.0529, 0.9471])

这里两者加和是1，才是正确的选择。

经验：

对于NLP而言，这两者之间确实有差别，Softmax的处理方式有时候会比Sigmoid的处理方式好一点。

对于CV而言，这两者之间也是有差别的，Sigmoid的处理方式有时候会比Softmax的处理方式好一点。

两者正好相反，这只是笔者的实验经验，建议大家两者都试试。

初识CV：目标检测比赛中的tricks（已更新更多代码解析）

初识CV：目标检测比赛笔记初识CV：图像分类比赛tricks：华为云人工智能大赛·垃圾分类挑战杯

初识CV：图像分类比赛tricks：“华为云杯”2019人工智能创新应用大赛

完整的图像分类代码和tricks：

https:// github.com/wusaifei/gar bage_classify

^[2]

我们以NLP中的Ner任务来说，假设模型是Bert，那模型的输出就是每个词的representation，比如是 $D=[128，1024]$ 这样的输出，那么这个时候如果我们需要做标注分类任务的时候，就需要先对这个”表示"进行处理。首先就是要做一个映射，映射到 $D = [128，10]$ 的空间，表明是个10分类，然后再进行归一化处理，比如用Softmax（多分类）、Sigmoid（单分类）等操作，最后再通过CrossEntropyLoss这样的函数做损失计算，下面是常用的一些函数的说明。先看下面这张表：

分类问题名称	输出层使用激活函数	对应的损失函数
二分类	sigmoid函数	二分类交叉熵损失函数BCELoss()--不带sigmoid 、BCEWithLogitsLoss()--带sigmoid
多分类	softmax函数	多类别交叉熵损失函数nn.NLLLoss()--不带LogSoftmax、 nn.CrossEntropy()--带LogSoftmax
多标签分类	sigmoid函数	二分类交叉熵损失函数 BCELoss()、BCEWithLogitsLoss()MultiLabelSoftMarginLoss()

首先介绍一下Softmax函数，Softmax函数输出的是概率分布，公式如下： $o(z_i)=softmax(z_i)=\frac{e^i}{\sum_je^j}\\$

其输出一定是在 $[0，1]$ 之间的，假如输入 $x=[1，2，13]$ ，那么Softmax之后的输出就是：

$x = [\frac{e^{1}}{e^1+e^2+e^{13}}，\frac{e^{2}}{e^1+e^2+e^{13}}，\frac{e^{13}}{e^1+e^2+e^{13}}] \approx [0,0,1]\\$

 代码如下 y = torch.rand(size=[2,3])  输出 >> tensor([[0.8101, 0.6255, 0.3686], [0.4457, 0.6892, 0.8240]]) net = nn.Softmax(dim=1)  dim根据具体的情况可选择 output = net(y)  输出 >> tensor([[0.4041, 0.3360, 0.2599], [0.2677, 0.3415, 0.3908]])

nn.Softmax可以用于激活函数或者多分类，其中分类模型如下：

 下面这段代码主要把softmax函数换成pytorch封装好的nn.Softmax函数即可，  不过通常情况下，我们对于多分类问题会直接选择使用nn.CrossEntropy()函数 def softmax(x): s = torch.exp(x) return s / torch.sum(s, dim=1, keepdim=True) def crossEntropy(y_true, logits): c = -torch.log(logits.gather(1, y_true.reshape(-1, 1))) return torch.sum(c) logits = torch.tensor([[0.5, 0.3, 0.6], [0.5, 0.4, 0.3]]) y = torch.LongTensor([2, 1]) c = crossEntropy(y, softmax(logits)) / len(y)

相对于nn.Softmax，nn.LogSoftmax多了一个步骤就是对输出进行了log操作，公式如下： $o(z_i)=log(softmax(z_i))=log(\frac{e^i}{\sum_je^j})\\$

nn.LogSoftmax输出的是小于0的数。

 代码如下 y = torch.rand(size=[2,3])  输出 >> tensor([[0.8101, 0.6255, 0.3686], [0.4457, 0.6892, 0.8240]]) net = nn.LogSoftmax(dim=1)  dim根据具体的情况可选择 output = net(y)  输出 >> tensor([[-0.9060, -1.0907, -1.3475], [-1.3179, -1.0744, -0.9396]])

nn.LogSoftmax的输出可以用于交叉熵损失函数的计算，对于额二分类和多分类的交叉熵计算公式如下：

$\begin{align*} & (二分类)L = \frac{1}{N}\sum_{i} L_i = -\frac{1}{N}\sum_{i}[y_i\cdot log(p_i) + (1-y_i)\cdot log(1-p_i)] \\ &(多分类)L = \frac{1}{N}\sum_{i} L_i = -\frac{1}{N}\sum_{i} \sum_{c=1}^My_{ic}\log(p_{ic}) \end{align*}\\$

其中：

- $y_i$ —— 表示样本i的label，正类为1，负类为0

- $p_i$ —— 表示样本i预测为正的概率

- $M$ ——类别的数量；

- $y_{ic}$ ——指示变量（0或1）,如果该类别和样本i的类别相同就是1，否则是0；

- $p_{ic}$ ——对于观测样本i属于类别 $c$ 的预测概率。

那nn.LogSoftmax就是在计算交叉熵log部分，nn.LogSoftmax()要和nn.NLLLoss()结合使用，NLLLoss()的计算公式如下：

$a=[a_0,a_1,...,a_{C-1}]$ 表示一个样本对每个类别的对数似然(log-probabilities)， $c$ 表示该样本的标签（比如1，2，-100等等），单个样本的损失函数公式描述如下:

$\begin{align*} &loss(a,c) = -w \cdot a[c] = -w log(p_c)\\ &其中， w = weight[c] \cdot 1\{c \ne ignore\_index \}\\ \end{align*}\\$

''' NLLLoss的类定义如下所示： torch.nn.NLLLoss(  weight=None,  ignore_index=-100,  reduction="mean", ) ''' import torch import torch.nn as nn model = nn.Sequential( nn.Linear(10, 3), nn.LogSoftmax() ) criterion = nn.NLLLoss() x = torch.randn(16, 10) y = torch.randint(0, 3, size=(16,)) # (16, ) out = model(x) # (16, 3) loss = criterion(out, y)

可参见nn.LogSoftmax下的说明，通常和LogSoftmax()结合一起使用

nn.CrossEntropyLoss用于计算多分类交叉熵损失，计算公式如下， $z=[z_0,z_1,...,z_{C-1}]$ 表示一个样本的非softmax输出(即logits输出)，c表示该样本的标签，则损失函数公式描述如下：

$loss(z,c)=-w \cdot log(\frac{e^{z[c]}}{\sum_{j=0}^{C-1}e^{z[j]}})\\ w = weight[c] \cdot 1\{c\ne ignore\_index \}$

由上可知，nn.CrossEntropyLoss是在一个类中组合了nn.LogSoftmax()和nn.NLLLoss()

''' 类定义如下 torch.nn.CrossEntropyLoss( weight=None, ignore_index=-100, reduction="mean", ) ''' import torch import torch.nn as nn model = nn.Linear(10, 3) criterion = nn.CrossEntropyLoss() x = torch.randn(16, 10) y = torch.randint(0, 3, size=(16,)) # (16, ) logits = model(x) # (16, 3) loss = criterion(logits, y)

Sigmoid多用于二分类或者多标签分类，Sigmoid的输出，每一维加起来不一定是和为1，也有可能输出的结果是 $[0.1，0.5，0.7]$ 这样子，所以这就可以进行多标签分类了，其公式如下： $sigmoid(z_i)=\frac{1}{1+e^{z_i}}\\$

 代码如下 y = torch.rand(size=[2,2])  输出 >> tensor([[0.7696, 0.5311], [0.8619, 0.8131]]) net = nn.Sigmoid() output = net(y)  输出 >> tensor([[0.6834, 0.6297], [0.7031, 0.6928]])

Sigmoid函数可以用于激活函数或者用于二分类、多标签，下面是Sigmoid和BCELoss()结合使用。

对于二分类而言，其中BCELoss()的计算方式如下，此时Sigmoid输出是1维的（见下面代码）：

用 $N$ 表示样本数量， $p_n$ 表示预测第 $n$ 个样本为正例的概率（经过sigmoid处理）， $y_n$ 表示第 $n$ 个样本的标签，

$loss(p, y) = \frac{1}{N}\sum_{n=1}^N-w_n(y_n * log( p_n )+ (1-y_n) * log(1 -p_n))\\ w = weight[c] \cdot 1\{c\ne ignore\_index \}$

对于多标签分类问题，对于一个样本来说，它的各个label的分数加起来不一定等于1（Sigmoid输出），BCELoss在每个类维度上求cross entropy loss然后加和求平均得到，这里就体现了多标签的思想。

 下面是 Sigmoid 二分类模型 import torch import torch.nn as nn model = nn.Sequential( nn.Linear(10, 1),  二分类 nn.Sigmoid() ) criterion = nn.BCELoss() x = torch.randn(16, 10) # (16, 10) y = torch.empty(16).random_(2) # shape=(16, ) 其中每个元素值为0或1 out = model(x) # (16, 1) out = out.squeeze(dim=-1) # (16, ) loss = criterion(out, y)  下面是 Sigmoid 多标签分类模型 import torch import torch.nn as nn model = nn.Sequential( nn.Linear(10, 3),  多分类 nn.Sigmoid() ) criterion = nn.BCELoss() x = torch.randn(16, 10) # (16, 10) y = torch.empty(16, 3).random_(2) # shape=(16, 3) 其中每个元素值为0或1，比如某一个样本是[1,0,1]  out = model(x) # (16, 3) loss = criterion(out, y)

下面直接使用BCEWithLogitsLoss()，这个类将Sigmoid()和BCELoss()整合起来，比纯粹使用BCELoss()+Sigmoid()更数值稳定。计算公式如下，其中 $z_n$ 表示预测第n个样本为正例的得分（没经过Sgmoid处理）， $y_n$ 表示第n个样本的标签， $\delta$ 表示sigmoid函数，则：

$loss(z, y) = \frac{1}{N}\sum_{n=1}^N-w_n(y_n * log(\delta( z_n) )+ (1-y_n) * log(1 -\delta(z_n)))\\ w = weight[c] \cdot 1\{c\ne ignore\_index \}$

import torch import torch.nn as nn model = nn.Linear(10, 1) criterion = nn.BCEWithLogitsLoss() x = torch.randn(16, 10) y = torch.empty(16).random_(2) # (16, ) out = model(x) # (16, 1) out = out.squeeze(dim=-1) # (16, ) loss = criterion(out, y)

nn.MultiLabelSoftMarginLoss() 和 nn.BCEWithLogitsLoss()没啥区别，唯一的区别就是nn.MultiLabelSoftMarginLoss()没有weighted参数

$loss(z, y) = \frac{1}{N}\sum_{n=1}^N-w_n(y_n * log(\delta( z_n) )+ (1-y_n) * log(1 -\delta(z_n)))\\$

import torch import torch.nn as nn model = nn.Linear(10, 1) criterion = nn.MultiLabelSoftMarginLoss() x = torch.randn(16, 10) y = torch.empty(16).random_(2) # (16, ) out = model(x) # (16, 1) out = out.squeeze(dim=-1) # (16, ) loss = criterion(out, y)

2021.7.6 追更...

参考文献：

从理论到实践解决文本分类中的样本不均衡问题-技术圈

本节主要从模型层面解决样本不均衡的问题。相比于控制正负样本的比例，我们还可以通过控制Loss损失函数来解决样本不均衡的问题。拿二分类任务来举例，通常使用交叉熵来计算损失，下面是交叉熵的公式：

上面的公式中y是样本的标签，p是样本预测为正例的概率。

1、类别加权Loss

为了解决样本不均衡的问题，最简单的是基于类别的加权Loss，具体公式如下：

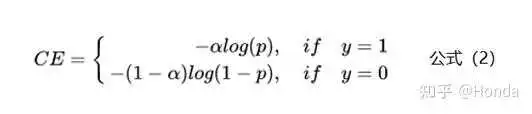
基于类别加权的Loss其实就是添加了一个参数a，这个a主要用来控制正负样本对Loss带来不同的缩放效果，一般和样本数量成反比。还拿上面的例子举例，有100条正样本和1W条负样本，那么我们设置a的值为10000/10100，那么正样本对Loss的贡献值会乘以一个系数10000/10100，而负样本对Loss的贡献值则会乘以一个比较小的系数100/10100，这样相当于控制模型更加关注正样本对损失函数的影响。通过这种基于类别的加权的方式可以从不同类别的样本数量角度来控制Loss值，从而一定程度上解决了样本不均衡的问题。

2、Focal Loss

上面基于类别加权Loss虽然在一定程度上解决了样本不均衡的问题，但是实际的情况是不仅样本不均衡会影响Loss，而且样本的难易区分程度也会影响Loss。下面是Focal Loss的计算公式：

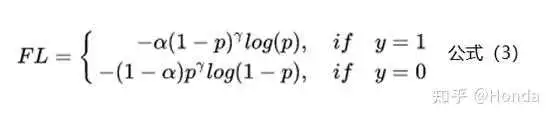
相比于公式2来说，Focal Loss添加了参数 $\gamma$ 从置信的角度来加权Loss值。假如 $\gamma$ 设置为0，那么公式3蜕变成了基于类别的加权也就是公式2；下面重点看看如何通过设置参数 $\gamma$ 来使得简单和困难样本对Loss的影响。当 $\gamma$ 设置为2时，对于模型预测为正例的样本也就是 $p>0.5$ 的样本来说，如果样本越容易区分那么 $1-p$ 的部分就会越小，相当于乘了一个系数很小的值使得Loss被缩小，也就是说对于那些比较容易区分的样本Loss会被抑制，同理对于那些比较难区分的样本Loss会被放大，这就是Focal Loss的核心：通过一个合适的函数来度量简单样本和困难样本对总的损失函数的贡献。关于参数 $\gamma$ 的设置问题，Focal Loss的作者建议设置为2。

下面是一个Focal Loss的实现，感兴趣的小伙伴可以试试，看能不能对下游任务有积极效果

3、GHM Loss

Focal Loss主要结合样本的难易区分程度来解决样本不均衡的问题，使得整个Loss的曲线平滑稳定的下降，但是对于一些特别难区分的样本比如离群点会存在问题。可能一个模型已经收敛训练的很好了，但是因为一些比如标注错误的离群点使得模型去关注这些样本，反而降低了模型的效果。比如下面的离群点图：

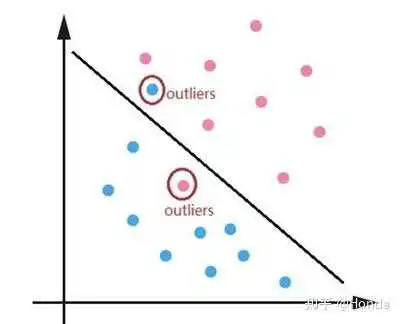
针对Focal Loss存在的问题，2019年论文《Gradient Harmonized Single-stage Detector》中提出了GHM(gradient harmonizing mechanism) Loss。相比于Focal Loss从置信度的角度去调整Loss，GHM Loss则是从一定范围置信度p的样本数量(论文中称为梯度密度)去调整Loss。理解GHM Loss的第一步是先理解梯度模长的概念，梯度模长 $g$ 的计算公式如下：

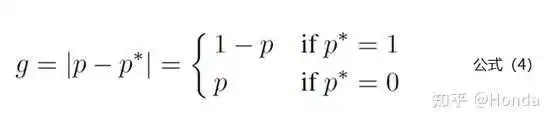
公式4中 $p$ 代表模型预测为1的概率值， $p^*$ 是标签值。也就是说如果样本越难区分，那么 $g$ 的值就越大。下面看看梯度模长 $g$ 和样本数量的关系图：

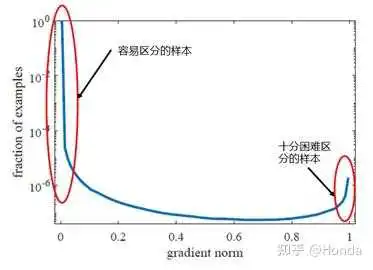
从上图中可以看出样本中有很大一部分是容易区分的样本，也就是梯度模长 $g$ 趋于0的部分。但是还存在一些十分困难区分的样本，也就是上图中右边红圈中的样本。GHM Loss认为不仅仅要多关注容易区分的样本，这点和Focal Loss一致，同时还认为需要关注那些十分困难区分的样本，因为这部分样本可能是标注错误的离群点，过多的关注这部分样本不仅不会提升模型的效果，反而还会有一定的逆向效果。那么问题来了，怎么同时抑制容易区分的样本和十分困难区分的样本呢？

针对这个问题，从上图中可以发现容易区分的样本和十分困难区分的样本都存在一个共同点：数量多。那么只要我们抑制一定梯度范围内数量多的样本就可以达到这个效果，GHM Loss通过梯度密度 $GD(g)$ 来表示一定梯度范围内的样本数量。这个其实有点像物理学中的密度，一定体积的物体的质量。梯度密度 $GD(g)$ 的公式如下：

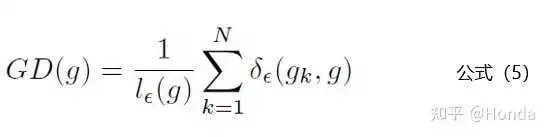
公式5中 $\delta_\epsilon(g_k,g)$ 代表样本中梯度模长 $g$ 分布在 $(g-\epsilon/2, g+\epsilon/2)$ 范围里面的样本的个数，代表了 $(g-\epsilon/2,g+\epsilon/2 )$ 区间的长度。公式里面的细节小伙伴们可以去论文里面详细了解。说完了梯度密度GD(g)的计算公式，下面就是GHM Loss的计算公式：

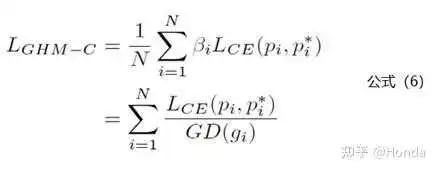
公式6中的Lce其实就是交叉熵损失函数，也就是公式1。下面是复现了GHM Loss的一个github上工程，有兴趣的小伙伴可以试试：https://github.com/libuyu/GHM_Detection

上溢出（overflow）和下溢出（underflow）是计算机科学中常见的问题，它们通常发生在浮点数运算中，特别是在执行复杂的数学计算时。当计算机试图计算一个数字的值超出了它能够存储的最大值（溢出上限）时，就会发生上溢出，而当计算机试图计算一个非常接近于零的数字时，可能会出现下溢出。

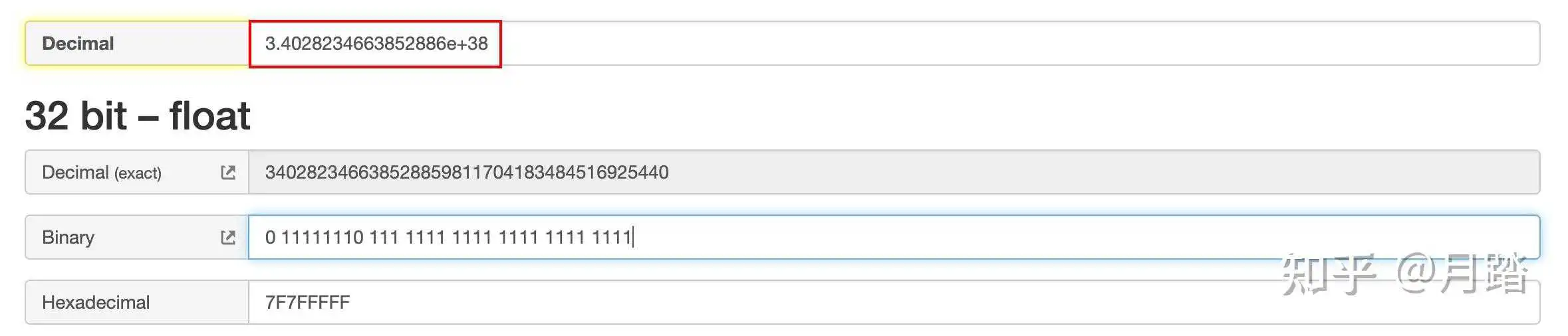
以IEEE754单精度浮点为例，它能表示的有效范围大致如下，其中的转换工具使用的这个网站：

Base Convert: IEEE 754 Floating Point

这种情况的符号位S=0，阶码E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为0 111 1111 1111 1111 1111 1111，那么最大正数值大约为3.e+38：

这种情况的符号位S=0，阶码E=1，指数e=1-127=-126，尾数M=0，其机器码为0 00000001 000 0000 0000 0000 0000 0000，那么最小正数大约为1.e−38：

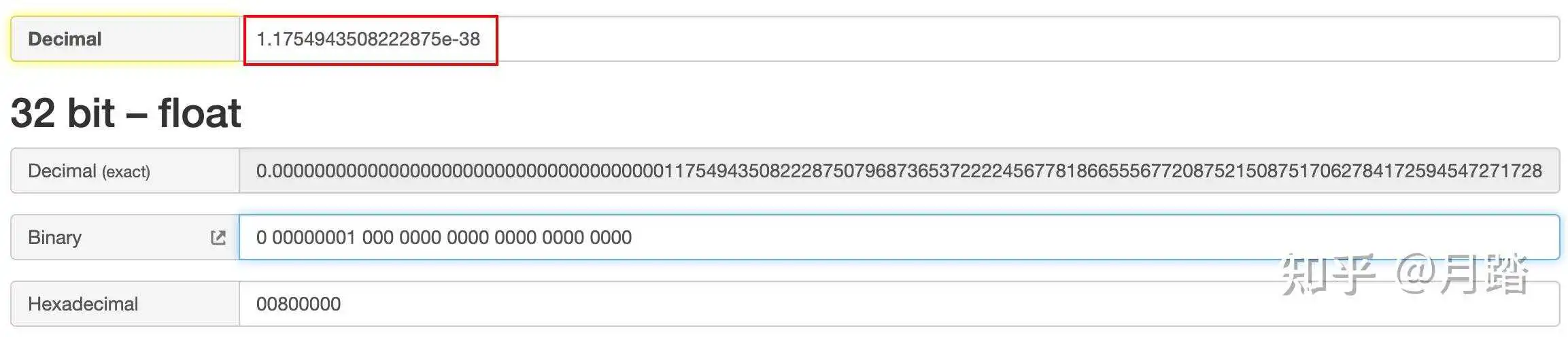
这种情况符号位S=1，阶码E=1，指数e=1-127==-126，尾数M=0，机器码与最小正数的符号位相反，其他均相同，为：1 00000001 000 0000 0000 0000 0000 0000，最大负数大约等于−1.e−38：

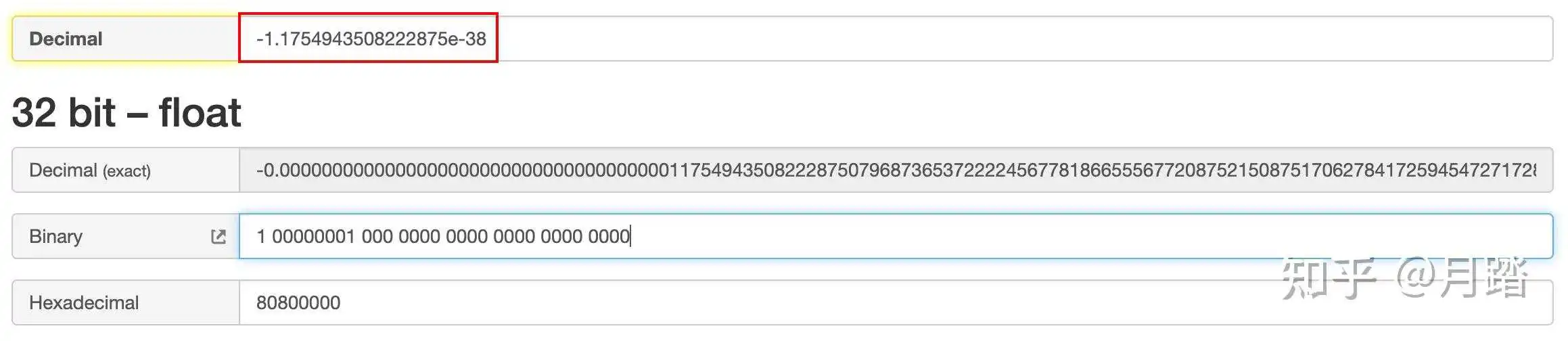
这种情况符号位S=0，阶码E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为：1 111 1111 1111 1111 1111 1111，最小负数大约等于-3.e+38：

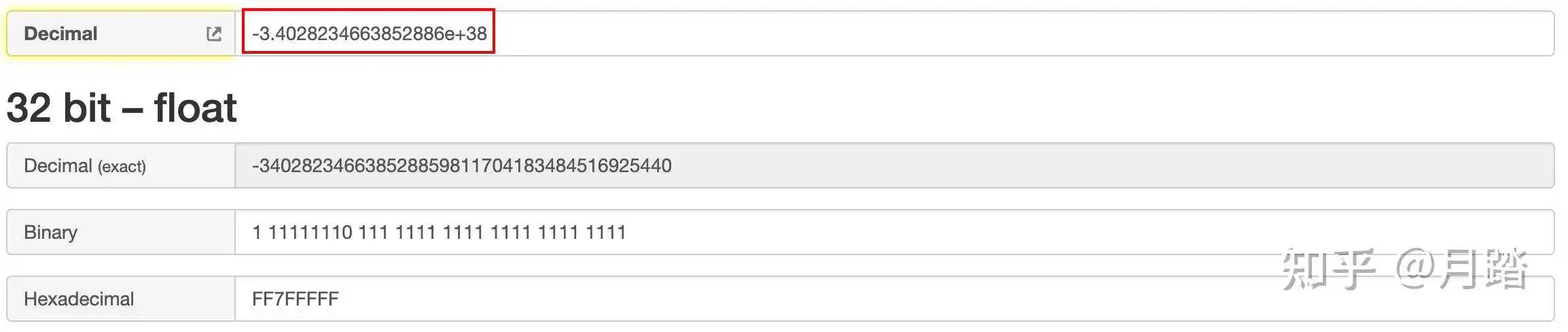
在深度学习中，由于涉及到大量的浮点数计算和指数运算，因此上溢出和下溢出经常会成为一个问题，例如，在 softmax 函数中，计算输入向量中的每一个元素的指数时，可能会因指数过大而导致上溢出，或者因指数太小而导致下溢出，这种数值计算中的问题被称为数值稳定性问题（numerical stability）。

先了解下softmax的概念，它可以将一个具有任意实数范围的向量归一化为一个概率分布，使得向量中的每一个元素都变成了 [0,1] 范围内的值，并且所有元素的和为 1，softmax 函数的作用可以总结为以下几点：

归一化：softmax 函数的主要作用是将输入向量归一化为一个概率分布，这使得模型的输出可以被解释为某种事件发生的概率。
解决互斥问题：对于一个具有 N 个类别的分类问题，softmax 函数可以将模型的输出归一化为一个 N 维概率向量。这个向量中的每个元素对应一个类别，且所有元素的和为 1。这种归一化方式可以确保输出值之间的互斥性，也就是说，只有一个类别能够被预测。
抑制强信号：对于一个输出向量，softmax 函数可以提高最大元素和其他元素之间的差距，从而使得最大值更加明显，其他值更加抑制，这样可以使得模型输出更加自信，从而更加确定预测结果。

再看下softmax的计算公式：

$\begin{equation} \sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \quad \text {for}\ i=1,2,\ldots,K \tag{1} \end{equation}$

为了更直观的展示公式1有可能出现的溢出问题，顺便贴下e的幂次方函数图像：

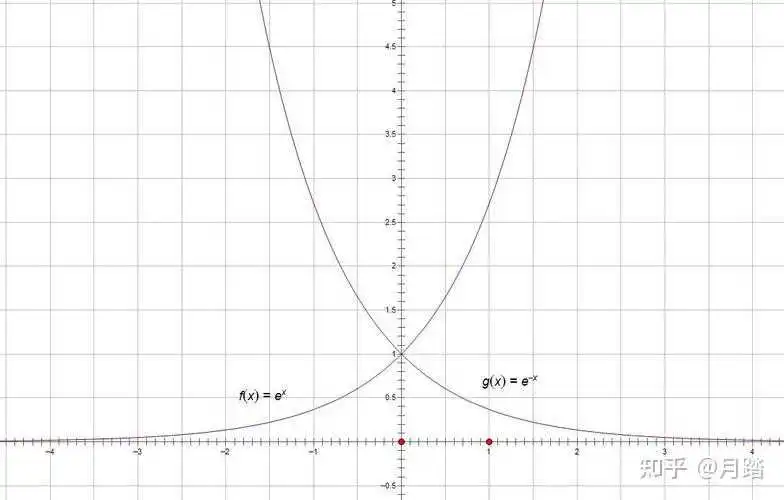
由图1和公式1，很容易得知在当指数部分大于38之后，就会引起单精度浮点数的上溢出，它的值会变成inf，同样由图2和公式1，很容易知道当指数部分在小于-38之后，就会引起单精度浮点数的下溢出，有一个很巧妙的恒等变换可以解决这两个问题，令：

$\begin{equation} M = max(z_{i}) \quad i=1,2,\ldots,K \tag{2} \end{equation}$

那么：

$\begin{equation} \sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} =\frac {\frac{e^{z_i}}{e^M}} {\frac{\sum_{j=1}^K e^{z_j}}{e^M}} =\frac {e^{z_i-M}} {\sum_{j=1}^K e^{z_j-M}} \tag{3} \end{equation}$

这里做了这个变换之后，指数部分的最大值为0，这样就解决了上溢出的问题

再来看下溢出的问题，对于公式3，因为M是zi的最大值，所以分母部分肯定大于等于1，这时候对于单个数值的e次幂，虽然仍然可能出现下溢出，即下面这种情况：

$\begin{equation} \lim_{\sigma \to 0}\frac{\sigma}{1+\sigma} \tag{4} \end{equation}$

这时候整个公式的结果为0，不会影响最终的结果的正确性

下面是一种考虑了数值稳定性的Naive实现：

#include <vector> #include <cmath>  std::vector<float> softmax(std::vector<float> input) { std::vector<float> output(input.size()); // 并找到input的最大值  float max_ele = input[0]; for (auto i = 1u; i < input.size(); i++) { if (input[i] > max_ele) { max_ele = input[i]; } } // 计算分母  auto sum = 0.f; for (auto i = 0u; i < input.size(); i++) { sum += exp(input[i] - max_ele); } // 计算Softmax函数的输出  for (auto i = 0u; i < output.size(); i++) { output[i] = exp(input[i] - max_ele) / sum; } return output; }

还可以用函数式编程的风格改写上面代码，即通过map和reduce两类操作来改写（关于map和reduce可以参考：C/C++杂谈：函数式编程）：

#include <iostream> #include <vector> #include <cmath> #include <algorithm> #include <numeric>  // 定义数值稳定的Softmax函数 std::vector<float> softmax(const std::vector<float> &input) { std::vector<float> output(input.size()); auto max_elem = *std::max_element(input.begin(), input.end()); auto sum = std::accumulate(input.begin(), input.end(), 0.f, [max_elem](float x, float y) { return x + std::exp(y - max_elem); }); std::transform(input.begin(), input.end(), output.begin(), [max_elem, sum](float x) { return std::exp(x - max_elem) / sum; }); return output; }

还可以继续通过模板把上面代码改成更加通用的形式：

#include <iostream> #include <vector> #include <cmath> #include <algorithm> #include <numeric>  // 定义数值稳定的Softmax函数 template<typename T> std::vector<T> softmax(const std::vector<T> &input) { std::vector<T> output(input.size()); auto max_elem = *std::max_element(input.begin(), input.end()); auto sum = std::accumulate(input.begin(), input.end(), T(0), [max_elem](const T x, const T y) { return x + std::exp(y - max_elem); }); std::transform(input.begin(), input.end(), output.begin(), [max_elem, sum](const T x) { return std::exp(x - max_elem) / sum; }); return output; }

Sigmoid是一种常用的激活函数，通常用于神经网络的输出层或者隐藏层中，数学上，Sigmoid及其导数的公式为：

$\begin{align} &f(x) = \frac{1}{1 + e^{-x}} \tag{5}\\ &f(x) = \frac{e^x}{e^x + 1} \tag{6}\\ &f'(x) = \frac{e^{x}}{(e^x + 1)^2}=f(x)(1-f(x)) \tag{7}\\ \end{align}$

对于公式5，当x趋近于正无穷大时，f(x)趋近于1；当x趋近于负无穷大时，f(x)趋近于0。这使得Sigmoid函数输出的值在0到1之间，非常适合作为概率或者激活值来使用。在神经网络中，Sigmoid函数可以帮助处理非线性的数据，提高了模型的复杂度和准确性，而且它的导数也有一个简单的表达式（如公式6所示），非常方便用于训练模型和反向传播算法。下面是公式5和公式6对应的函数图像：

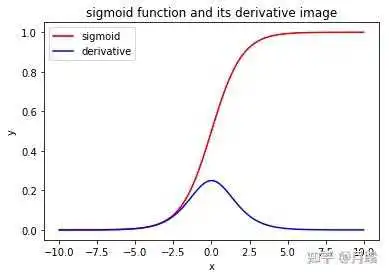
由图5和公式5，可知当x小于0之后，e的-x次方很容易出现inf，这就会导致上溢出，解决办法就是在x小于0时，采用公式6进行计算，这时虽然会产生下溢出，但是可以保证数值稳定性，下面是相应的代码实现：

#include <iostream> #include <cmath> #include <limits>  using namespace std; float sigmoid(float x) { if (x >= 0) { float z = exp(-x); return 1.f / (1.f + z); } else { float z = exp(x); return z / (1.f + z); } }

实际上对于公式5，即使e的-x次方出现了inf，这时候是1除以无穷大，仍然可以得到正确的结果0，这个很容易可以做实验，C++有表示无穷的方法，如下所示：

cout << 1.f / std::numeric_limits<float>::infinity() << endl;

真正有可能出问题的是公式6，如果e的x次方出现了inf，那么将会出现无穷大除以无穷大，这是一个不定式，仍然可以用上面代码做实验：

cout << std::numeric_limits<float>::infinity() / std::numeric_limits<float>::infinity() << endl;

结果会输出-nan，nan是not a number的简写，即无效数字，除此之外，浮点0除以浮点0、0乘以无穷等情况也都会得到nan，无论如何，我们使用上面的改进过的sigmoid的实现，可以保证sigmoid运算的数值稳定性。

tanh又叫做双曲正切函数，和sigmoid一样，它也常用作激活函数，它的输出范围为[-1,1]，输入小于0时逼近于-1，输入大于0时逼近于1，下面是具体的数学公式：

$\begin{align} &f(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \tag{8}\\ &f(x) = \frac{e^{2x}-1}{e^{2x} + 1} \tag{9}\\ &f(x) = \frac{1-e^{-2x}}{1+e^{-2x} } \tag{10}\\ &f'(x) = 1-f(x)^2 \tag{11}\\ \end{align}$

函数图像如下：

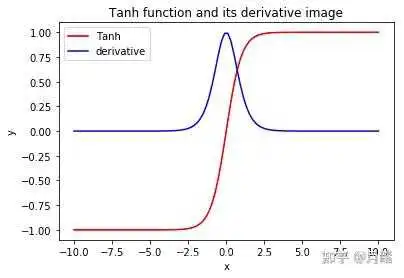
由前面章节的分析，如果使用公式8，很容易出现上溢出，解决办法就是把公式变换成公式9和公式10，当x小于0的时候采用公式9计算，当x大于0的时候采用公式10计算，相关代码如下：

float tanh(float x) { if(x < 0) { float z = exp(2*x); return (z - 1) / (z + 1); } else { float z = exp(-2*x); return (1 - z) / (1 + z); } }

本文详细分析了softmax、sigmoid、tanh的数值稳定性问题，以及解决办法，下面是本文参考的内容：

Base Convert: IEEE 754 Floating Point
IEEE754 32位浮点数表示范围
C/C++杂谈：函数式编程
如何防止softmax函数上溢出(overflow)和下溢出(underflow)
Sigmoid Tanh and Relu 原函数导函数图像python绘制

到此这篇sigmoid函数求导（sigmoid函数求导范围）的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章，希望大家都能在编程的领域有一番成就！

上一篇：淘宝优先支付方式怎么设置（淘宝优先支付方式怎么设置密码）

下一篇： argsort用法（argsort函数作用）

版权声明：
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/30060.html

相关文章：