您在上一个练习中了解到，仅向网络添加隐藏层不足以表示非线性关系。对线性运算执行的线性运算仍然是线性的。
如何配置神经网络来学习值之间的非线性关系？我们需要找到一种将非线性数学运算插入模型的方法。
如果这看起来有点熟悉，那是因为我们在本课程的早些部分实际上就对线性模型的输出应用了非线性数学运算。在逻辑回归模块中，我们通过将模型的输出通过 S 型函数传递，使线性回归模型输出介于 0 到 1 之间的连续值（表示概率）。
我们可以将同样的原则应用于神经网络。我们来回顾一下之前的练习 2 中的模型，不过这次，在输出每个节点的值之前，我们先应用 S 型函数：
您可以点击 >| 按钮（位于播放按钮右侧），逐步执行每个节点的计算。在图表下方的计算面板中，查看计算每个节点值所执行的数学运算。请注意，每个节点的输出现在是上一层节点线性组合的 sigmoid 转换，并且输出值均压缩在 0 到 1 之间。
在这里，S 型函数用作神经网络的激活函数，用于对神经元的输出值进行非线性转换，然后将该值作为输入传递给神经网络下一层的计算。
现在，我们添加了激活函数，添加层会产生更大的影响。通过将非线性叠加到非线性上，我们可以对输入和预测输出之间的非常复杂的关系进行建模。简而言之，每一层都会针对原始输入有效地学习更复杂、更高级别的函数。如果您想更直观地了解其运作方式，请参阅 Chris Olah 的优秀博文。
常用作激活函数的三个数学函数是 Sigmoid 函数、tanh 函数和 ReLU 函数。
S 型函数（如上文所述）对输入 $x$ 执行以下转换，从而生成一个介于 0 到 1 之间的输出值：
[F(x)=frac{1} {1+e^{-x}}]
下面是该函数的图表：
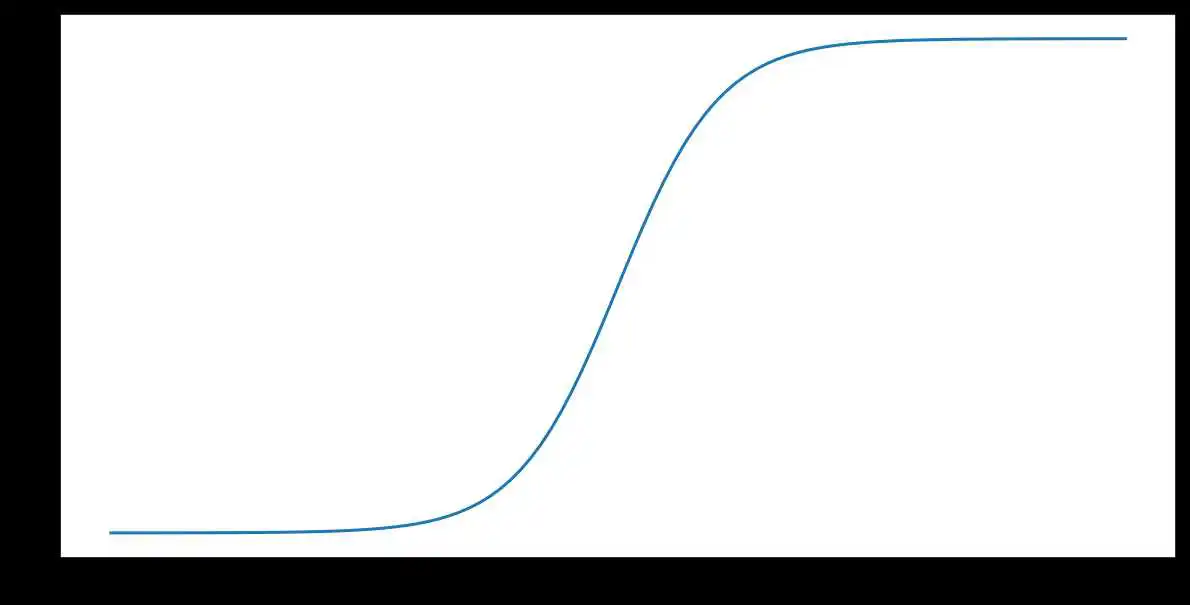
tanh（简称“双曲正切”）函数会转换输入 $x$，以生成介于 -1 和 1 之间的输出值：
[F(x)=tanh(x)]
以下是此函数的图表：
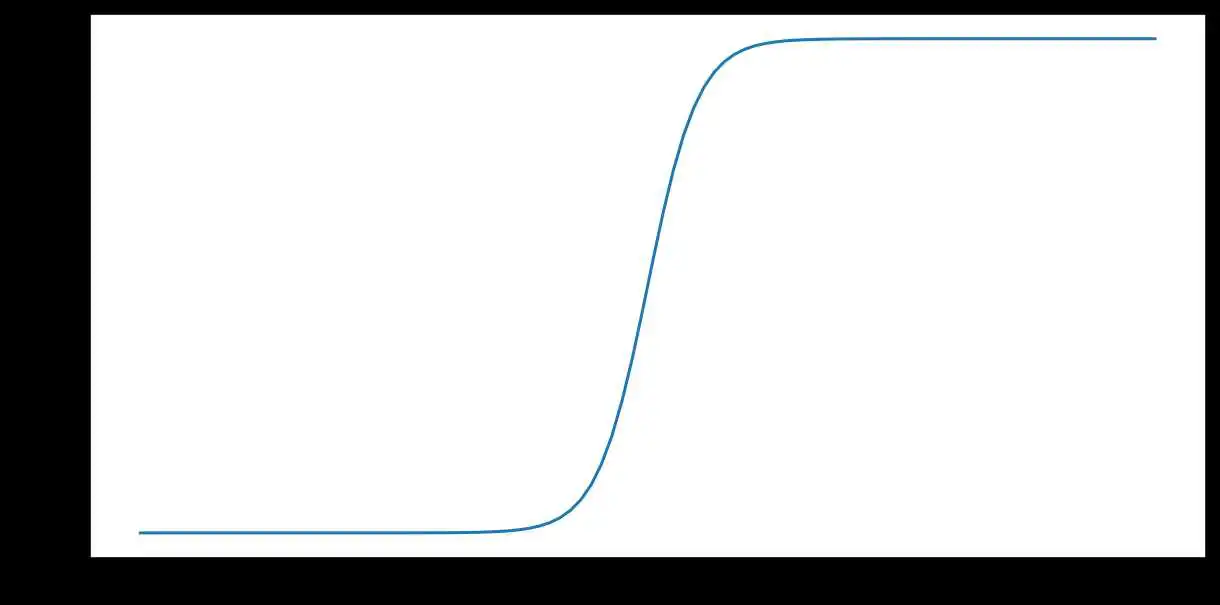
修正线性单元激活函数（简称 ReLU）使用以下算法转换输出：
- 如果输入值 $x$ 小于 0，则返回 0。
- 如果输入值 $x$ 大于或等于 0，则返回输入值。
可以使用 max() 函数以数学方式表示 ReLU：
下面是该函数的图表：
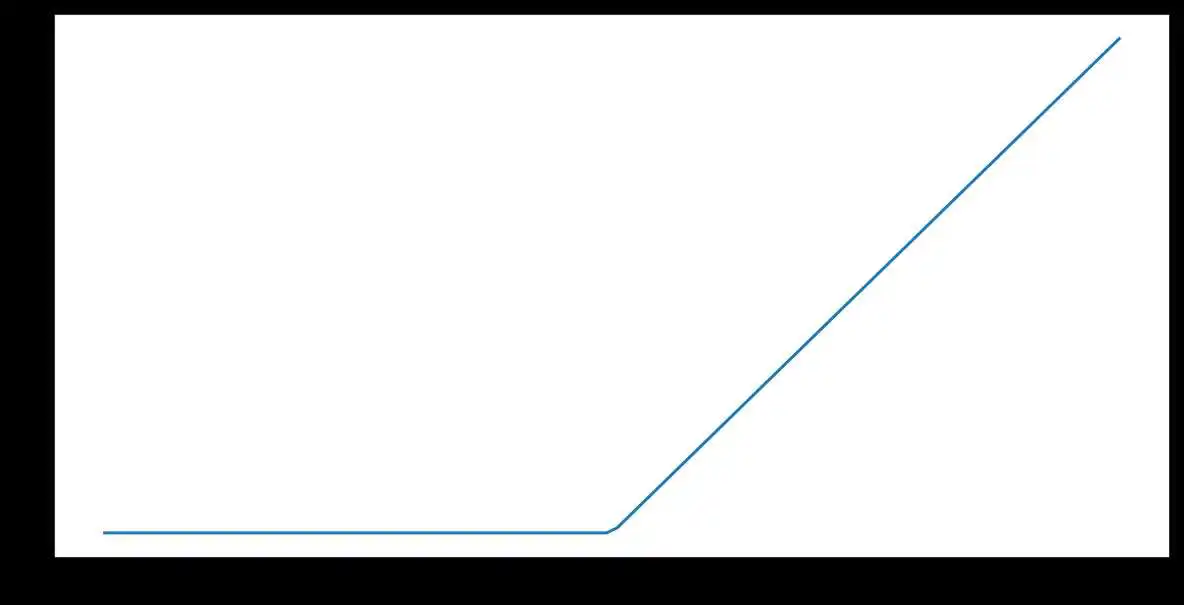
ReLU 作为激活函数的效果通常优于 S 型函数或 tanh 等平滑函数，因为它在神经网络训练期间不易受到梯度消失问题的影响。与这些函数相比，ReLU 的计算也更容易。
在实践中，任何数学函数都可以用作激活函数。假设 (sigma) 代表我们的激活函数。网络中节点的值由以下公式给出：
Keras 为许多激活函数提供开箱即用型支持。尽管如此，我们仍建议您先从 ReLU 开始。
以下视频回顾了您迄今为止学到的有关神经网络构建方式的所有内容：
现在，我们的模型包含人们通常在提及神经网络时所指的所有标准组件：
- 一组节点，类似于神经元，并且位于层中。
- 一组权重，表示每个神经网络层与其下方的层之间的关系。下方的层可能是另一个神经网络层，也可能是其他类型的层。
- 一组偏差，每个节点一个偏差。
- 一个激活函数，对层中每个节点的输出进行转换。不同的层可能拥有不同的激活函数。
反向传播是神经网络最常用的训练算法。它使梯度下降法可用于多层神经网络。许多机器学习代码库（例如 Keras）会自动处理反向传播算法，因此您无需自行执行任何底层计算。请观看以下视频，从概念上大致了解反向传播算法的工作原理：
本部分介绍了反向传播的失败情况，以及正则化神经网络的最常用方法。
较低神经网络层（更接近输入层）的梯度可能会变得很小。在深度网络（包含多个隐藏层的网络）中，计算这些梯度可能涉及对许多小项进行乘法。
当较低层的梯度值接近 0 时，梯度会被称为“消失”。具有消失梯度的层训练速度非常慢，或者根本无法训练。
ReLU 激活函数有助于防止梯度消失。
如果网络中的权重非常大，则较低层的梯度涉及许多大项的乘积。在这种情况下，可能会出现梯度爆炸：梯度太大而无法收敛。
批处理归一化有助于防止梯度爆炸，降低学习率也有助于防止梯度爆炸。
一旦 ReLU 单元的加权和低于 0，ReLU 单元可能会卡住。它会输出 0，对网络的输出没有任何贡献，并且在反向传播期间梯度无法再流经它。由于梯度源被切断，ReLU 的输入可能永远不会发生足够的变化，无法使加权和重新高于 0。
降低学习率有助于防止 ReLU 单元死亡。
还有一种正则化形式，称为Dropout 正则化，对神经网络很有用。其工作原理是，在一个梯度步长中随机“丢弃”网络中的单元激活。丢弃的样本越多，正则化效果就越强：
- 0.0 = 不进行 dropout 正规化。
- 1.0 = 舍弃所有节点。模型学不到任何规律。
- 0.0 和 1.0 之间的值更有用。
在下面的互动练习中，您将进一步探索 神经网络。首先，您将看到参数和超参数如何变化 会影响网络的预测。然后，您将利用学到的知识来 来拟合非线性数据。
以下 widget 会设置具有以下配置的神经网络：
- 包含 3 个神经元的输入层，分别包含值 、 和
- 包含 4 个神经元的隐藏层
- 包含 1 个神经元的输出层
- ReLU 激活函数应用于 所有隐藏层节点和
查看广告联盟的初始设置（注意：请勿点击 ▶️ 或 >| 按钮），然后完成该微件下方的任务。
神经网络模型的三个输入特征的值 。点击网络中的每个节点， 值。在点击“播放”(▶️) 按钮之前，请先回答以下问题：
现在，点击网络上方的播放 (▶️) 按钮，然后观察所有隐藏层 和输出节点值进行填充。以上答案正确吗？
您获得的确切输出值因 和偏差参数会随机初始化。不过，由于每个神经元 的权重值是 0， 隐藏层节点值都将清零。例如，第一个 隐藏层节点的计算公式为：
y = ReLU(w11* 0.00 + w21* 0.00 + w31* 0.00 + b)
y = ReLU(b)
因此，每个隐藏层节点的值都等于 偏差 (b)，如果 b 为负值，则值为 0；如果 b 为 0，则值为 b 本身； 积极。
然后，输出节点的值将按如下方式计算：
y = ReLU(w11* x11 + w21* x21) + w31* x31 + w41* x41 + b)
在修改神经网络之前，请先回答以下问题：
现在，修改神经网络以添加一个包含 3 个节点的新隐藏层，如下所示：
- 点击文本 1 个隐藏层左侧的 + 按钮，添加新层 隐藏层。
- 点击新隐藏层上方的 + 按钮两次可再添加 2 个节点 传递给层。
以上答案正确吗？
只有输出节点会发生变化。因为这种神经网络的推理 为“前馈”（计算从开始到结束），加上 只会影响新层的节点， 而不是其前面的层。
点击网络第一个隐藏层中的第二个节点（从顶部开始） 图表。在对网络配置进行任何更改之前，请先回答 以下问题：
现在，点击权重 w12（显示在 第一个输入节点 x1），将其值更改为 ，然后按 Enter 键。 观察图表的更新。
您的答案正确吗？验证答案时要小心：如果节点 值没有变化，这是否意味着基础计算没有变化？
在第一个隐藏层中，唯一受影响的节点是第二个节点（ ）。第一个 隐藏层未包含 w12 作为参数，因此它们 。第二个隐藏层中的所有节点都会受到影响， 取决于第一个节点中第二个节点的值 隐藏层。同样，输出节点值也会受到影响， 则取决于第二个隐藏层中节点的值。
您是否认为答案是“无”因为这个 Deployment 中的 网络在您更改权值时发生了变化？请注意，底层的 的计算可能会在不改变节点值的情况下 （例如，ReLU(0) 和 ReLU(-5) 产生的输出均为 0。 不要仅仅假设网络受到的影响 查看节点值请务必查看计算结果
在特征交叉练习中， 请参阅“分类数据”模块 您手动构建了特征组合来拟合非线性数据。 现在，看看你能否构建一个 如何在训练期间拟合非线性数据。
您的任务：配置一个能够将橙点与白点分开的神经网络 下图中的蓝点，两者的损失都小于 0.2 训练数据和测试数据。
说明：
在下面的互动式 widget 中：
- 使用一些超参数进行实验，从而修改神经网络超参数 以下配置设置之一：
- 通过点击 + 和 - 按钮来添加或移除隐藏层： （位于网络图中隐藏层标题的左侧）。
- 点击 + 和 - 在隐藏层中添加或移除神经元 按钮。
- 通过从学习速率中选择新值来更改学习速率 下拉菜单。
- 更改激活函数，方法是从 激活下拉菜单。
- 点击图表上方的播放 (▶️) 按钮可训练神经网络 使用指定的参数训练该模型。
- 观察与训练数据拟合的模型的可视化效果 以及 测试损失和 训练损失值，位于 输出部分。
- 如果模型在测试和训练数据上的损失达不到 0.2， 点击“重置”，然后以不同的一组配置重复执行第 1-3 步 设置。重复此过程，直至达到您期望的结果。
我们通过以下方式使测试损失和训练损失均低于 0.2：
- 添加了 1 个包含 3 个神经元的隐藏层。
- 将学习速率设为 0.01。
- 选择 ReLU 的激活函数。
您之前遇到了 二元分类 可以从两个可能的选项中选择其一，例如：
- 指定电子邮件是垃圾邮件还是非垃圾邮件。
- 特定肿瘤是恶性或良性的。
在本节中，我们将介绍 多类别分类 模型，并从多种可能性中进行选择。例如：
- 这只狗是小猎犬、巴吉度猎犬还是寻血猎犬？
- 这朵花是西伯利亚鸢尾、荷兰鸢尾、蓝旗鸢尾吗？ 还是矮胡须鸢尾？
- 那架飞机是波音 747、空客 320、波音 777 还是 Embraer 190？
- 这是一张苹果、熊、糖果、狗还是鸡蛋的图片？
现实世界中的一些多类别问题需要从数百万个类别中进行选择 不同类别的组合。以多类别分类为例， 该模型可识别几乎任何事物的图像。
本部分详细介绍了多类别分类的两个主要变体：
- 一对多
- one-vs.-one，通常称为 softmax
一对多提供了一种使用二元分类的方法 以跨多个可能的标签进行一系列是或否预测。
假设某个分类问题有 N 种可能的解决方案，即一对多 包含 N 个独立的二元分类器 - 一个二元分类器， 来预测每个可能的结果。在训练期间，模型会运行 一系列二元分类器，对每个分类器进行训练， 分类问题。
例如，假设有一张水果的图片， 可能会训练不同的识别器，每个识别器都会回答不同的是或否 问题：
- 这是一张苹果的图片吗？
- 这张图片是橙色的吗？
- 这是一张香蕉的图片吗？
- 这张图片是葡萄吗？
下图说明了在实践中的运作方式。
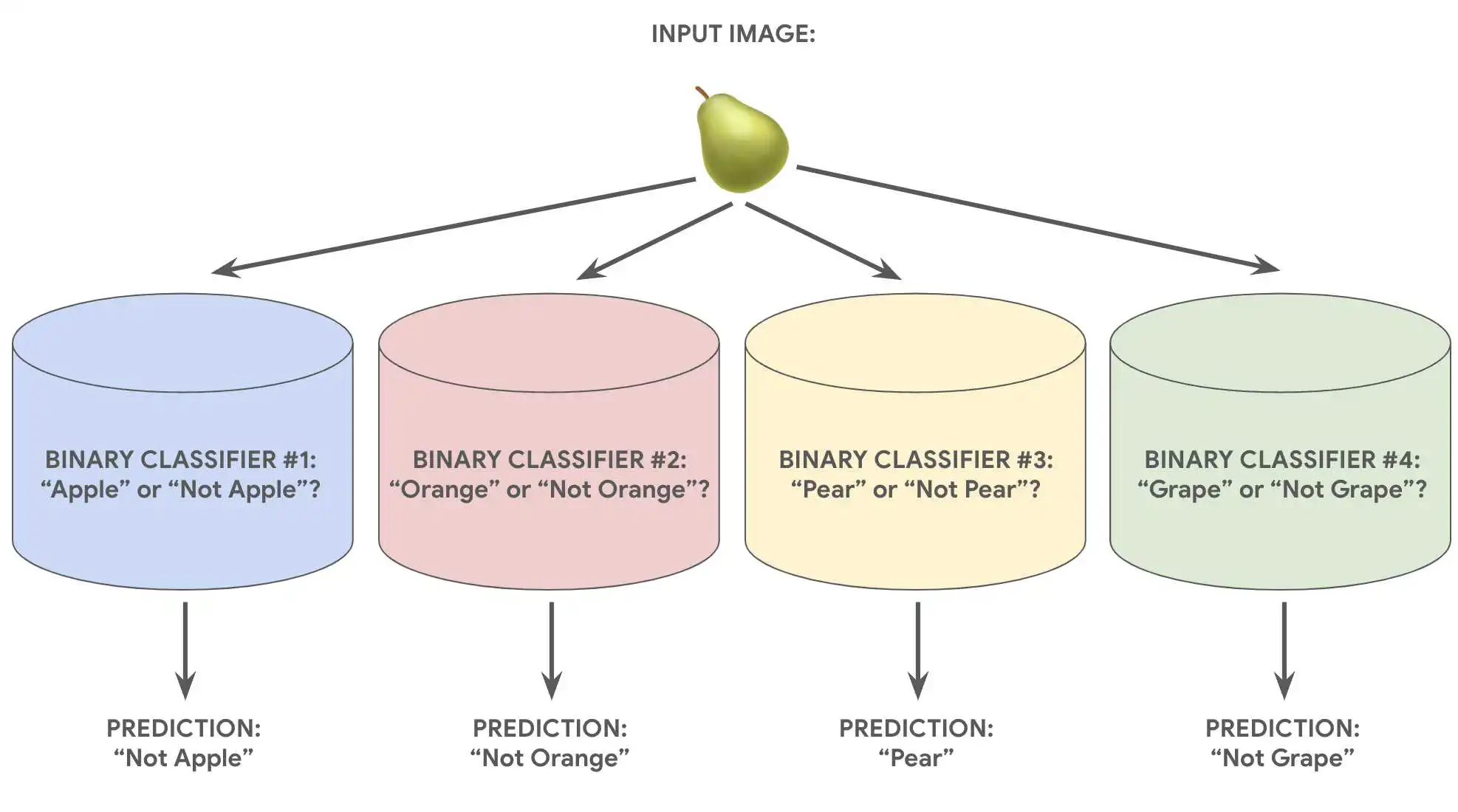
这种方法相当合理， 很小，但随着类别数量的增加， 。
我们可以创建一个更加高效的一对多模型 深度神经网络，其中每个输出节点表示不同的 类。下图演示了此方法。
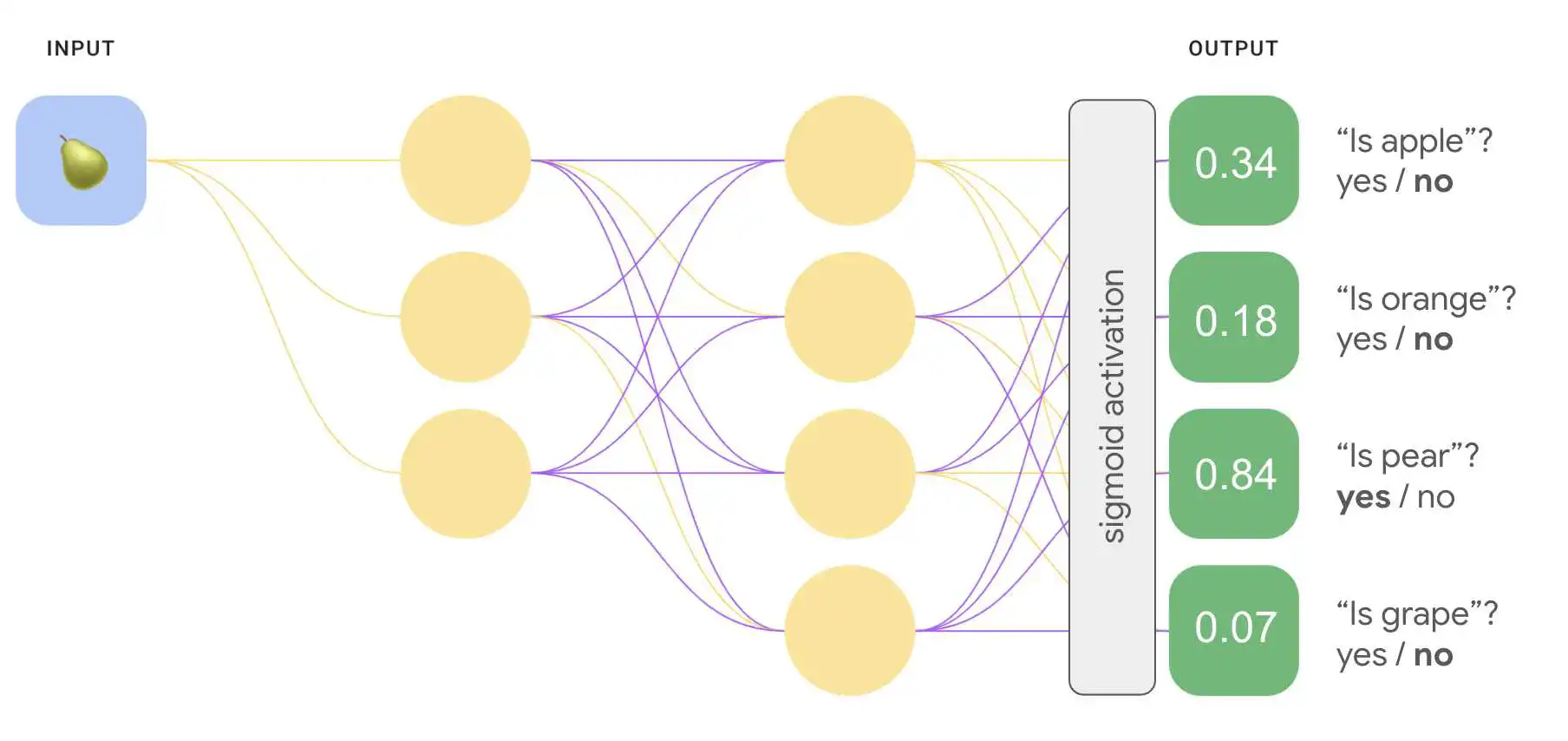
您可能已经注意到，图 8 输出层中的概率值 总和不是 1.0（或 100%）。（实际上，两者的总和为 1.43。）在“一对多”模式中 方法时，每个二元结果集的概率 而不会影响所有其他数据集也就是说，我们要确定 的“apple”与“非 Apple”而不会考虑 水果选项：“橙色”“梨”或“葡萄”。
但是，如果我们想要预测每种水果 相互比较？在本示例中，我们不再预测“apple”与“非 “apple”，我们想要预测“apple”还是“橙色”与“pear”以及“葡萄”字样。 这种类型的多类别分类称为一对一分类。
我们可以使用同一类型的神经元， 用于一对多分类的网络架构，具有一个关键更改。 我们需要对输出层应用不同的转换。
对于一对多，我们将 S 型激活函数应用于每个输出 这样，每个节点的输出值都介于 0 到 1 之间 节点，但无法保证这些值的总和正好为 1。
对于一对一运算，我们可以应用一个名为 softmax 的函数， 向多类别问题中的每个类别分配以小数表示的概率， 所有概率相加之和为 1.0。这一附加限制条件 有助于训练过程比其他方式更快收敛。
下图重新实现了我们的一对多多类别分类。 一对一任务的形式来表示。请注意，为了执行 softmax， 位于输出层正前面的层（称为 softmax 层）必须具有 与输出层相同数量的节点。
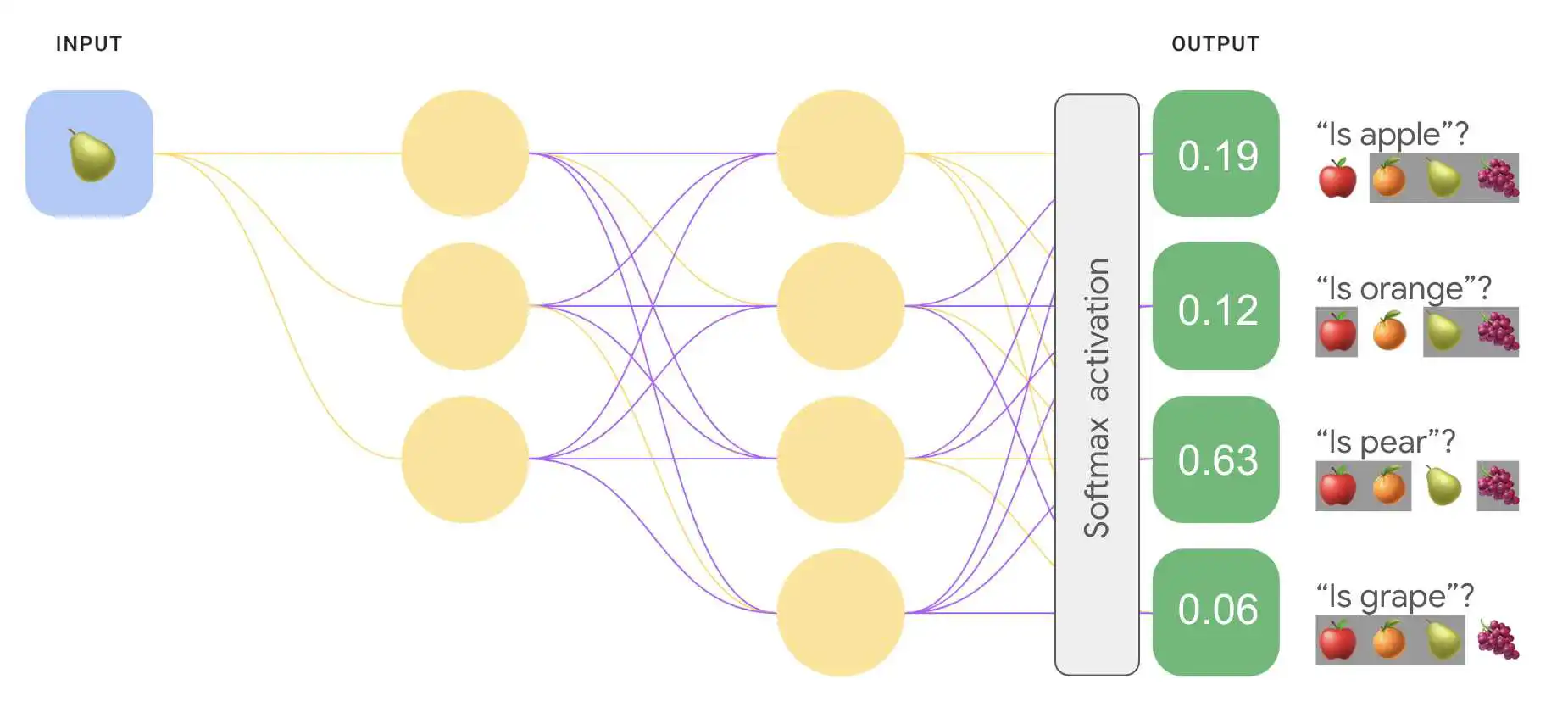<ph type="x-smartling-placeholder">
请考虑以下 softmax 变体：
- 完整 softmax 是我们一直以来讨论的 softmax；即 softmax 会计算每个可能的类别的概率。
- 候选采样是指 softmax 计算概率的 但仅随机抽取一个样本， 负标签。例如，如果我们想要确定 无论输入图片是小猎犬还是寻血猎犬，我们都不必 为每个非狗狗样本提供概率。
当类别数很小时，完整 softmax 的开销很小 但随着类别数量的增加，费用会变得非常高。 候选采样可以提高 类别数量。
Softmax 假设每个样本只是一个类别的成员。 不过，一些样本可以同时是多个类别的成员。 对于此类示例：
- 您不能使用 softmax。
- 您必须依赖于多个逻辑回归。
例如，上面图 9 中的 1:1 模型假设每个输入 图片只能描绘一种水果：苹果、橙子、梨子或梨子 一颗葡萄。然而，如果输入图片可能包含多种类型的水果， 就要同时装有苹果和橙子，这时就要用到 回归。
到此这篇sigmod激活函数（sigmod激活函数的输入）的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章，希望大家都能在编程的领域有一番成就！版权声明：
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！
转载请注明出处，原文链接：https://www.xkablog.com/haskellbc/26439.html