Logarithmic Differentiation
(对数求导)



 取以其它常数为底数的对数也不影响最终结果。接下来,我们对取完对数的式子进行隐函数求导的计算(implicit differentiation),可以得到:
取以其它常数为底数的对数也不影响最终结果。接下来,我们对取完对数的式子进行隐函数求导的计算(implicit differentiation),可以得到:

 在等式两端同时乘以y,便可以得到:
在等式两端同时乘以y,便可以得到:

 替换掉y,可以得到最终答案:
替换掉y,可以得到最终答案:

 并利用原函数的表达式替换掉
并利用原函数的表达式替换掉  , 我想计算它的导数,但此时我们无法直接使用指数函数或者对数函数的求导公式。 利用logarithmic differentiation,可以较为便捷地得到这个函数的导数表达式:
, 我想计算它的导数,但此时我们无法直接使用指数函数或者对数函数的求导公式。 利用logarithmic differentiation,可以较为便捷地得到这个函数的导数表达式:

Newton’s Method
(牛顿法)

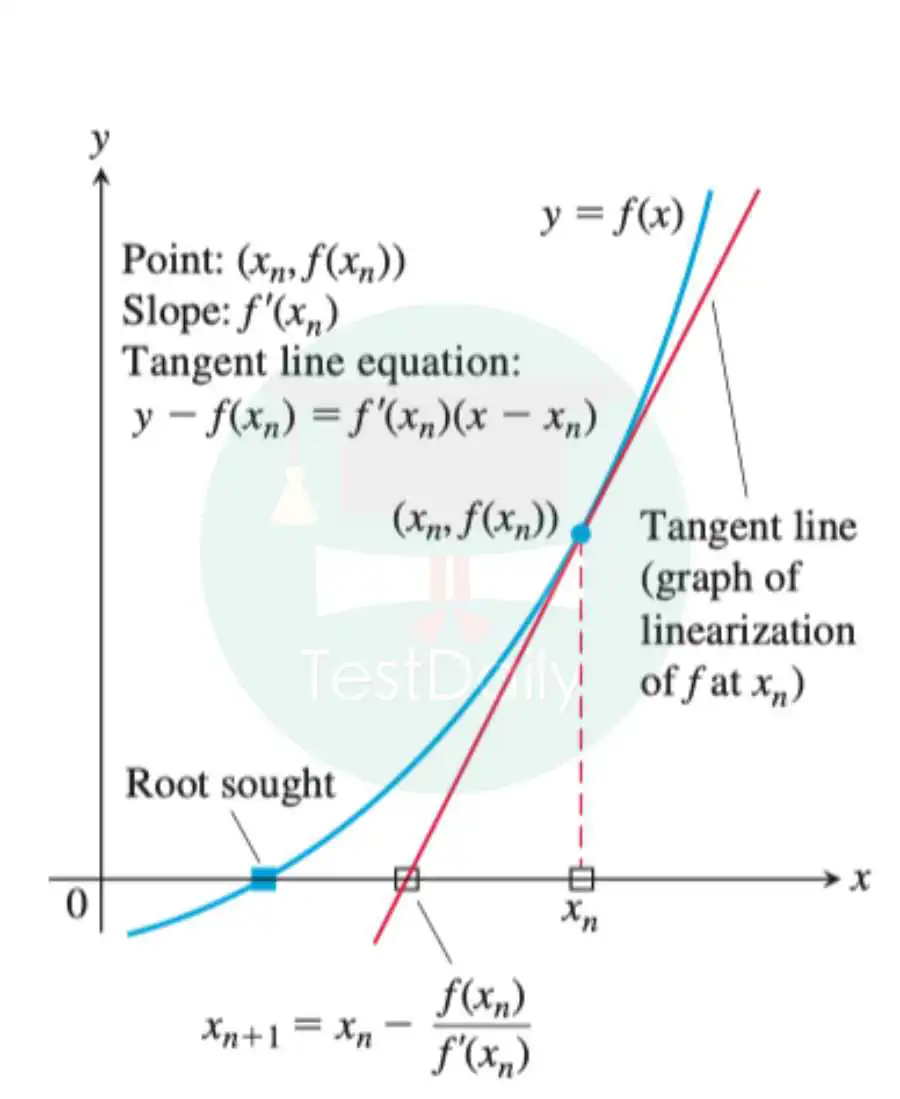
 , 我想找到它的正零点,需要求出
, 我想找到它的正零点,需要求出  时的
时的  但在计算器发明之前,人们如何能求出
但在计算器发明之前,人们如何能求出  , 为了计算方便,我在此处令
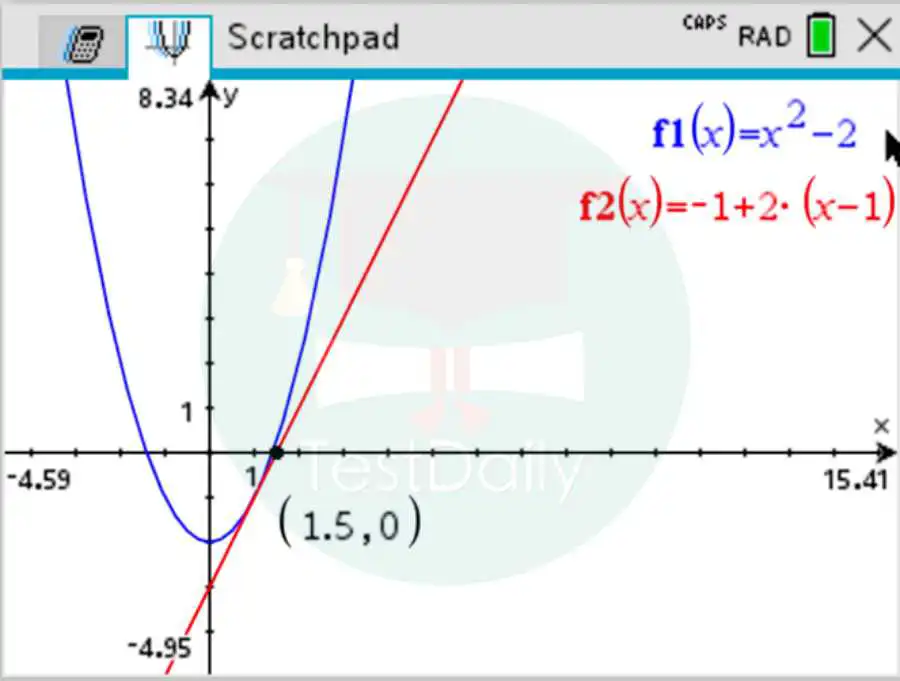
, 为了计算方便,我在此处令  ,然后写出函数在
,然后写出函数在 处的切线方程,
处的切线方程,  。接下来再找到这个切线与
。接下来再找到这个切线与
 处的切线方程,
处的切线方程,  。接下来接再找到这个切线与轴的交点约为
。接下来接再找到这个切线与轴的交点约为 
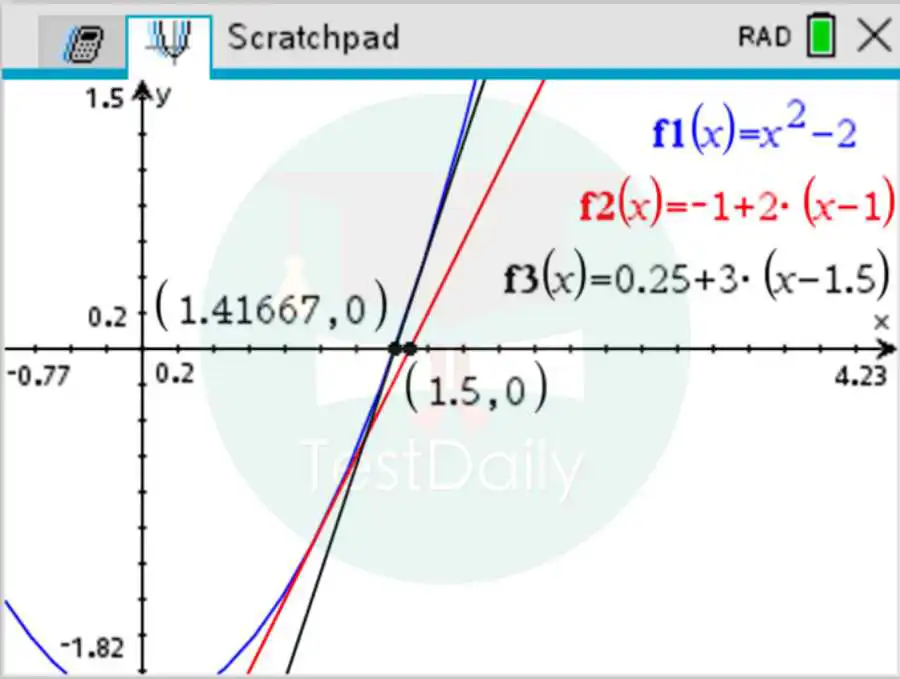
 。然后然后写出函数在
。然后然后写出函数在  处的切线方程,
处的切线方程,  。接下来接再找到这个切线与轴的交点约为
。接下来接再找到这个切线与轴的交点约为 
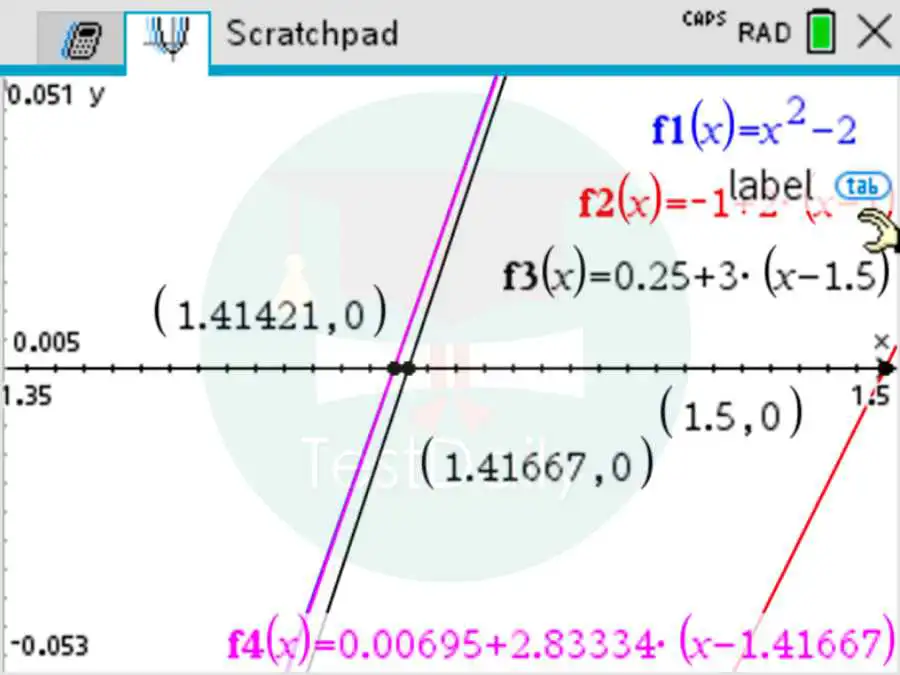
 处的切线方程
处的切线方程  接下来令
接下来令  找到它和
找到它和
 在处的切线所近似出的零点,我们让它等于
在处的切线所近似出的零点,我们让它等于
 便可以让这一估值过程重复下去,由此可得出Newton’s Method的一般流程:
便可以让这一估值过程重复下去,由此可得出Newton’s Method的一般流程:

鉴于篇幅所限,我将在接下来的系列文章中继续分享剩余的几个知识点,包括Simpson Rule, Differentials, Shell Method,Root Test,敬请关注。
本文作者

TD福利
为了帮助大家解决AP微积分在学习过程中常遇到的共性问题,TD AP数学教研组的老师们凭借多年教学经验,精心总结了历年考生在AP微积分学习与考试中常犯的二十余个错误,编纂成《AP微积分易错点合集》。
这本书按照AP微积分官方考试大纲的知识点顺序编排,覆盖了极限、微分、积分、参数方程与极坐标等内容,既指出了学生常犯的共性问题,也提供了易错点的正确解答过程。

《AP微积分易错点合集》封面预览
正在备考AP微积分的同学们千万不要放过这本宝藏典籍!只需扫描下方二维码,添加小马甲微信并发送暗号「微积分易错点」即可免费领取「TD原创AP微积分易错点合集」啦~

版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/haskellbc/18939.html
