注意: 是不会自动过滤掉空格 和回车的 的。
- $double$ 对应 ,$float$ 对应 。
- 中, 通杀单精度和双精度;在 中, 和 才有区别。为什么呢?
- 的 标识符的确既可以输出浮点数又可以输出双精度数。根据 “缺省参数扩展”规则, 不论范围内有没有原形都会在在类似 的可变长度参数列表中采用, 浮点型的变量或扩展为双精度型, 因此 只会看到双精度数。
- ,它接受指针,这里没有类似的类型提升。(通过指针)向 $float$ 存储和向 $double$ 存储大不一样,因此, 区别 和 。
AcWing 604. 圆的面积
浮点数保留位数时用 和,保留五位可以写成 。
- 小时:
- 分钟:求剩余分钟数,然后再
- 秒: 求剩余秒数
AcWing 654. 时间转换
- 求持续时间时,可以统一成分钟,用 ,再计算小时和分钟。第二讲较难题 AcWing 668. 游戏时间2
求两数的最大值,公式:$max (a, b) = frac{(a + b + abs(a - b))}{2}$
- 判断一个数是否是另一个的整数倍:
- 判断 a, b, c 是否能构成三角形:
AcWing 672. 税 (y总解法比较好)
有三个整数 $a, b, c$
- $if (a > b)$,交换 $a$, $b$
- $if (a > c)$,交换 $a$, $c$
- $if (b > c)$,交换 $b$, $c$
从而得到 $a <= b <= c$
如何交换两个数?
如果要输入的数很多的话,可以用循环来输入:
在 100 个数中找出最大值,代码模板:
AcWing 721. 递增序列
的两种处理方式:
- 中间用逗号 隔开
- ,然后里面写退出条件
AcWing 720. 连续整数相加
AcWing 722. 数字序列和它的和
AcWing 723. PUM
AcWing 718. 实验
C++ 的运算能力
- C++ 一秒钟内大概最多可以计算 $1$ 亿 ($10^8$) 次,每次循环 100 次,所以总共要计算 $1$ 亿 $ imes 100$,超出运算能力了。
- 如果开方优化后,$10^8$ 开方为 $10^4$ 次,每次循环 100 次,所以最多运算 $10^6$ 次,即 $100$ 万次。
如果 $d$ 能整数 $x$ ,那么 $frac{x}{d} $ 也能整除 $x$ 。
例:对于 $12$ 来说,$2$ 是 $12$ 的约数,$6$ 也是 $12$ 的约数;
又 $3$ 是 $12$ 的约数,$4$ 也是 $12$ 的约数;
所以我们只要枚举较小的那个约数即可。
$d le frac{x}{d}$
$d^{2} le x$
$d le sqrt{x}$
AcWing 725. 完全数
AcWing 726. 质数
AcWing 727. 菱形
曼哈顿距离:横坐标的差的绝对值 和纵坐标的差的绝对值的和。
$(x1, y1)、 (x2, y2)$
曼哈顿距离 = $|x1 - x2| + |y1 - y2|$
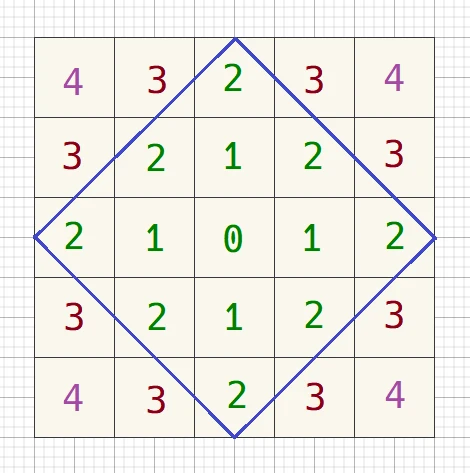
22.1 二维数组求右上半部分
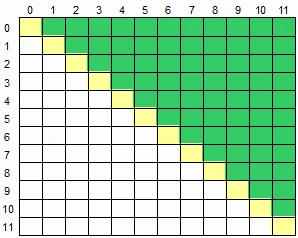
22.2 二维数组求左上半部分
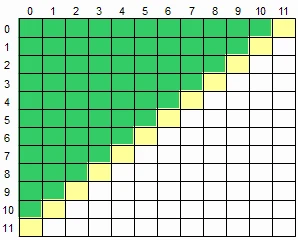
22.3 二维数组求左下半部分
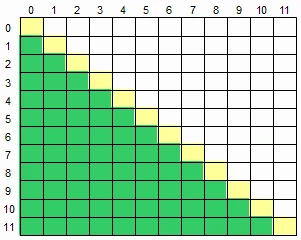
22.4 二维数组求右下半部分
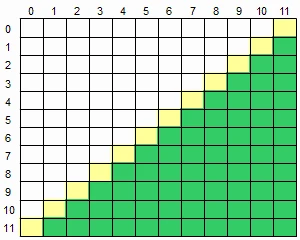
23.1 二维数组的上方区域
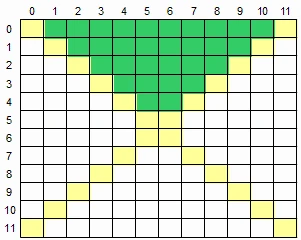
AcWing 742. 最小数和它的位置
27.1 AcWing 753. 平方矩阵 I

27.2 AcWing 754. 平方矩阵 II
先确定左上右下的对角线,然后再按下图规律填充矩阵:
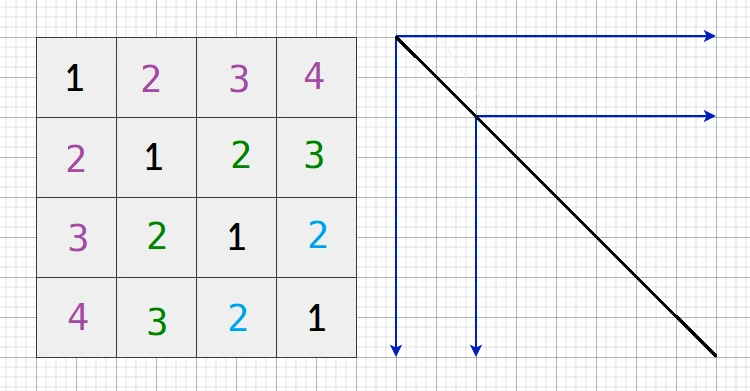
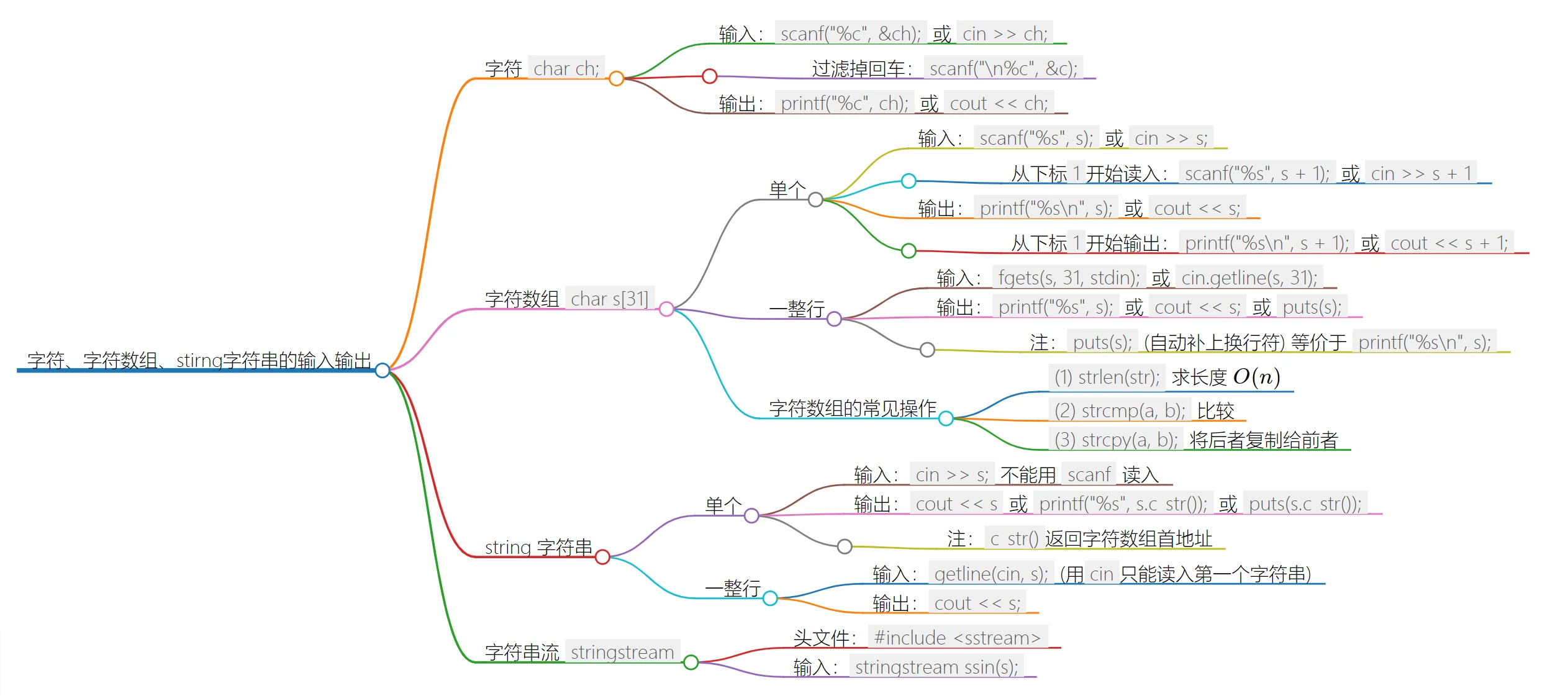
- 特殊值: 是 $65$ ~ $92$, 是 $97$ ~ $122$, 是 $48$ ~ $57$。
- 强制转换:
AcWing 764. 输出字符串
- 字符串就是字符数组加上结束符
- 可以使用 字符串 来初始化 字符数组,但此时要注意,每个字符串结尾会暗含一个 字符,因此字符数组的长度至少要比字符串的长度多 $1$
注意: 和 都是读到 或 为止
输入
- 读入字符数组时, 无须加取址符号 ,因为变量 本身就是个地址。
- 输入也可以用
- 如果想读到从下标 开始的话,写成
输出
- 可以用
- 也可以写成
- 如果想从下标 或 开始,则写成 (从下标开始输出) 或
(1) 字符数组 用 或 输入;输出也可以用
- 这里的 是把标准读入当成文件来读入。
- 输出除了用 也可以用 ,等价于 它会自动补上换行符
- 输入会自动加上回车,所以用 (输出自带回车) 的话会多一个回车
(2) 字符串 用 输入
- 如果是整行 类型的字符串,则用 来输入
- 如果是单个 类型,用读入,不能用 读入
AcWing 766. 去掉多余的空格
字符串用读会去掉多余空格
- 下面几个函数需要引入头文件:
- (1) ,求字符串的长度,只计算字符串的元素,不计入其中
- (2) ,比较两个字符串的大小,$a < b$ 返回 $-1$,$a == b$ 返回 $0$,$a > b$ 返回 $1$。这里的比较方式是字典序!
- (3) ,将字符串 $b$ 复制给从 $a$ 开始的字符数组。
- (4) 遍历字符数组中的字符
注意:如果没先存 而写成 ,那么就两重循环了。
经典题:给定一个只包含小写字母的字符串,请你找到第一个仅出现一次的字符。如果没有,输出“no”。
AcWing 772. 只出现一次的字符
因为字符数组最后是 ,所以循环条件写成如下即可
经典题:密码翻译,输入一个只包含小写字母的字符串,将其中的每个字母替换成它的后继字母,如果原字母是’z’,则替换成’a’。
AcWing 767. 信息加密
难题:字符串模拟题
AcWing 87. 把字符串转换成整数
- //将字符串转换成数字
- //将字符数组转换成数字
- 可变长的字符序列,可以动态分配,比字符数组更加好用。需要引入头文件:
- 可将两个字符串拼接在一起
- 不能用 来读入 ,这是错的;只能用 来读入
- 不能用 直接输出 ,需要写成:
返回的是字符数组的首地址
- 使用 读取一整行
- 的 和 操作。是 $O(1)$ 复杂度, 是 $O(n)$ 的复杂度。
- 做加法运算时,字面值和字符都会被转化成 对象,因此直接相加就是将这些字面值串联起来
- 当把 对象和字符字面值及字符串字面值混在一条语句中使用时,必须确保每个加法运算符的两侧的运算对象至少有一个是
难题:AcWing 763. 循环相克令
举例:左旋转字符串:
输入:”abcdefg” , n=2
输出:”cdefgab”
AcWing 773. 字符串插入
- 用 输入字符数组时,还要记得去掉末尾回车
- 用 输入字符数组时,不用做这步操作
难题:AcWing 768. 忽略大小写比较字符串大小
用 输入字符数组:
用 输入字符数组:
- 输入会自动带上回车,如果再用 输出(自动带上回车),就有两个回车了,多出一个回车
AcWing 815. 打印字符串
- ,字符 的 ASCII 码是 $65$, 的 ASCII 码是 $97$,它们之间相差 $32$,所以
AcWing 770. 单词替换
头文件定义了三个类型来支持内存 IO,这些类型可以向 string 写入数据,从 string 读取数据,就像 string 是一个 IO流一样。
- 从 string 读取数据
- 向 string 写入数据
- 头文件 用于读写给定 string 的字符串流,既可从 string 读数据也可向 string 写数据
AcWing 771. 字符串中最长的连续出现的字符
AcWing 775. 倒排单词
字符串数组有别于字符数组,定义字符串数组
可以先用 读入,统计
倒排单词可以倒序排,输出
AcWing 776. 字符串移位包含问题
类似技巧的难题:AcWing 778. 字符串最大跨距
- 这道题是让我们求几次方 $n$ 最大值,可以把字符串当成周期串来处理
- $len$ 是字符串总长,假定最大周期是 $n$,最小单位子串的长度为 $m = len/n$
- 可以采用倒序 再 ,找到最大周期 $n$ 就可以 跳出
- 一个条件是
- 设单位子串为
- 如果将单位子串循环 $n$ 遍后得到的字符串等于 $str$,说明 $n$ 是我们要求的最小周期
- 输出 $n$,并 跳出即可
难题:AcWing 777. 字符串乘方
难题:AcWing 779. 最长公共字符串后缀
AcWing 819. 递归求阶乘
AcWing 820. 递归求斐波那契数列
AcWing 32. 调整数组顺序使奇数位于偶数前面
AcWing 818. 数组排序 (01:00)
AcWing 823. 排列
函数
AcWing 51. 数字排列
和 基本相同。里面的 和 可以不写,在 中,不写默认是 ,但子啊 中不写默认是 。
- 代码是存到内存空间里的,所有的函数调用都是在栈空间里,局部变量都是定义到栈空间里的,静态变量和数组全部定义到堆空间里。
- 局部变量是随机的,全局变量全是 ;这是因为开到栈里的空间变量没有赋值,所以是不确定的;开到堆里的空间变量全部默认为 。
引用、取地址符;指针、解引用符
- 在声明语句中, 和 用于组成复合类型;( 引用, 指针)
- 在表达式中,它们的角色又转变成运算符。( 取地址符, 解引用符)
- 指针指向存放变量的值的地址。因此我们可以通过指针来修改变量的值。
- 数组名是一种特殊的指针。指针可以做运算:
方法:先让该节点伪装成其next节点6变成8,再把next节点干掉(真正的8被干掉)
AcWing 66. 两个链表的第一个公共结点
是变长数组,支持随机访问,不支持在任意位置 $O(1)$ 插入。为了保证效率,元素的增删一般应该在末尾进行。
头文件 主要包括循环队列 和优先队列 两个容器。
声明:
- 除了队列、优先队列、栈之外,其他所有的STL容器都有 函数。
- 重新初始化队列可以清空:
容器是一个键值对 $key-value$ 的映射,其内部实现是一棵以 $key$ 为关键码的红黑树。$Map$ 的 $key$ 和 $value$ 可以是任意类型,其中 $key$ 必须定义小于号运算符。
AcWing 20. 用两个栈实现队列
AcWing 75. 和为S的两个数字
AcWing 26. 二进制中1的个数
- 做法
AcWing 862. 三元组排序
- 的十进制是 $$,也就是 $10^{9}$ 级别的(和 一个数量级),而一般场合下的数据都是小于 $10^{9}$ 的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
- 另一方面,由于一般的数据都不会大于 $10^{9}$,所以当我们把无穷大加上一个数据时,它并不会溢出(这就满足了“无穷大加一个有穷的数依然是无穷大”),事实上 + $= $,这非常大但却没有超过 32-bit int的表示范围,所以 还满足了我们“无穷大加无穷大还是无穷大”的需求。
- 最后, 还能给我们带来一个意想不到的额外好处:如果我们想要将某个数组清零,我们通常会使 用 这样的代码来实现(方便而高效),但是当我们想将某个数组全部赋值为无穷大时(例如解决图论问题时邻接矩阵的初始化),就不能使用memset函数而得自己写循环了,我们知道这是因为 是按字节操作的,它能够对数组清零是因为 $0$ 的每个字节都是 $0$,现在好了,如果我们将无穷大设为 ,那么奇迹就发生了, 的每个字节都是 !所以要把一段内存全部置为无穷大,我们只需要 。所以在通常的场合下, 真的是一个非常棒的选择。
- 另外两种常见的方式: 和 $memset$ 是按字节赋值的,$int$ 是四个字节的。前者,往每个字节赋值 $0$,那每个字节就是 $0$;后者,$-1$ 在 C++ 表示的时候,表示每个位上的数字都是 $1$,把每个字节赋值成 $-1$,那整个就是 $-1$。
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/do-docker-k8s/20095.html
