



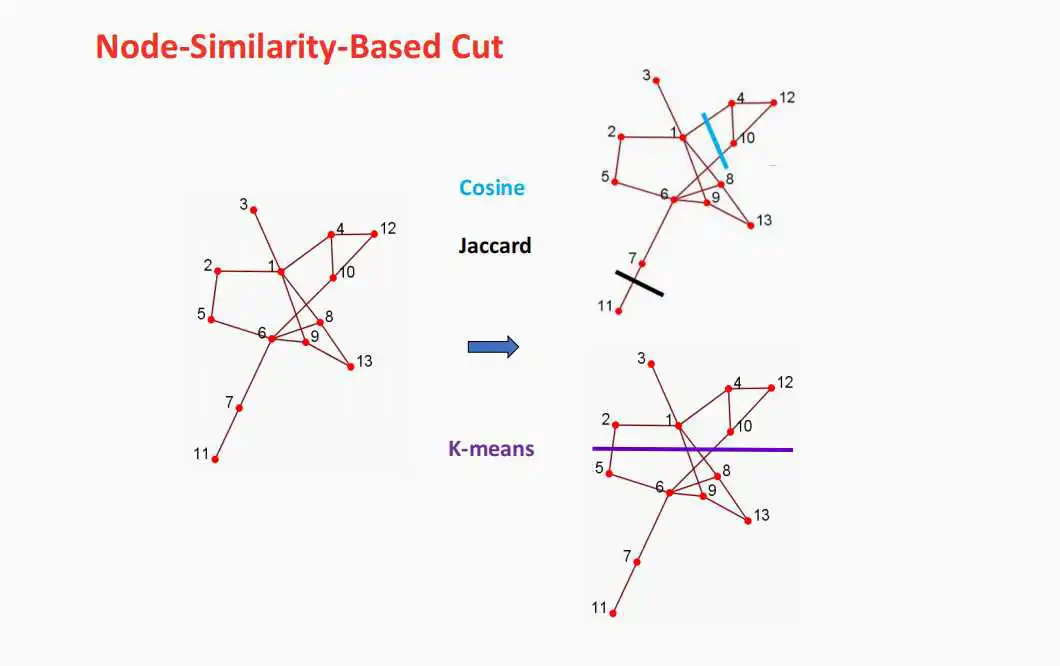
 图12
图12
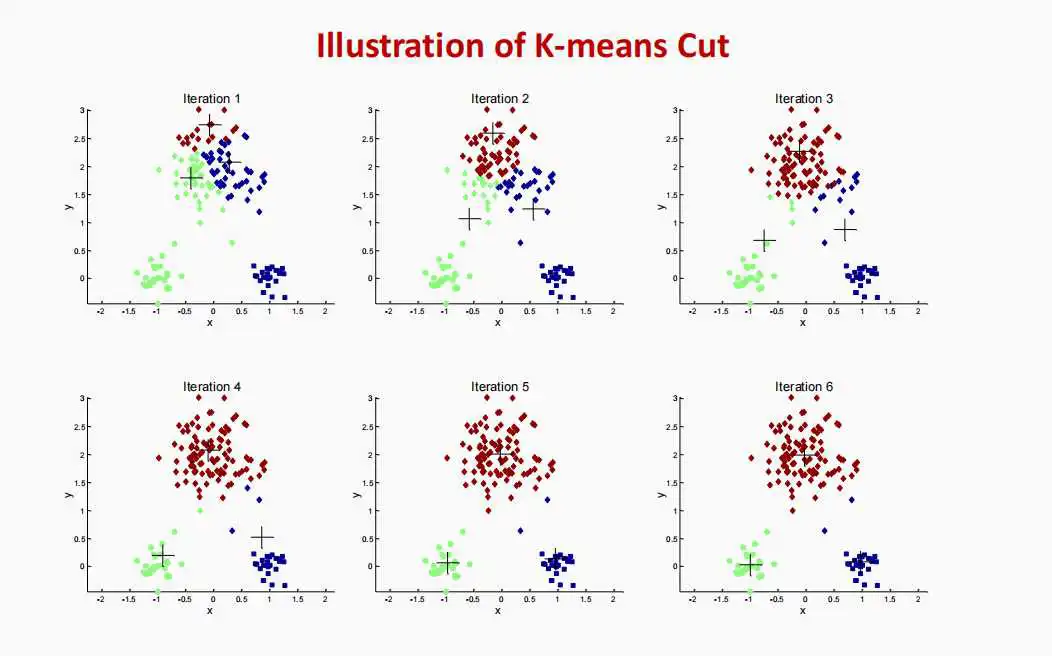
 图14
图14




- 陈关荣丨图论基础第二期(上)
- 陈关荣丨图论基础第二期(下)
- 陈关荣丨网络基本模型与拓扑特征分析(下)

版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/14992.html
