bfs广度优先搜索（广度优先搜索使用的辅助空间是什么）



和树的遍历类似，图的遍历也是从图中某点出发，然后按照某种方法对图中所有顶点进行访问，且仅访问一次。

但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻，所以在图的遍历中必须记录已被访问的顶点，避免重复访问。

根据搜索路径的不同，我们可以将遍历图的方法分为两种：

• 广度优先搜索
• 深度优先搜索。

顶点对(u，v)是无序的，即（u，v）和（v，u）是同一条边。常用一对圆括号表示。

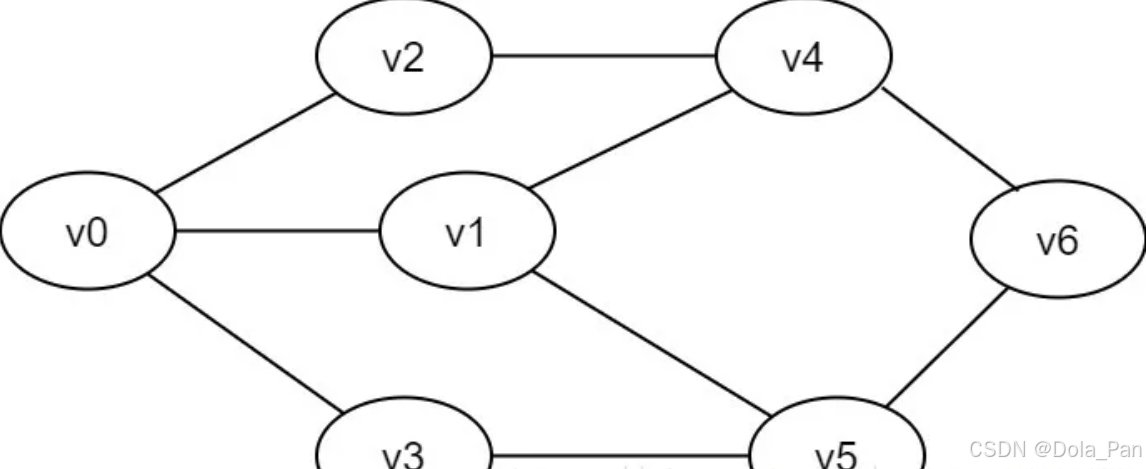
图2-1-1 无向图示例

顶点对<u,v>是有序的，它是指从顶点u到顶点 v的一条有向边。其中u是有向边的始点，v是有向边的终点。常用一对尖括号表示。

图2-1-2 有向图示例

图的每条边上可能存在具有某种含义的数值，称该数值为该边上的权。而这种带权的图被称为网。

连通图：在无向图G中，从顶点v到顶点v'有路径，则称v和v'是联通的。若图中任意两顶点v、v'∈V，v和v'之间均联通，则称G是连通图。上述两图均为连通图。

非连通图：若无向图G中，存在v和v'之间不连通，则称G是非连通图。

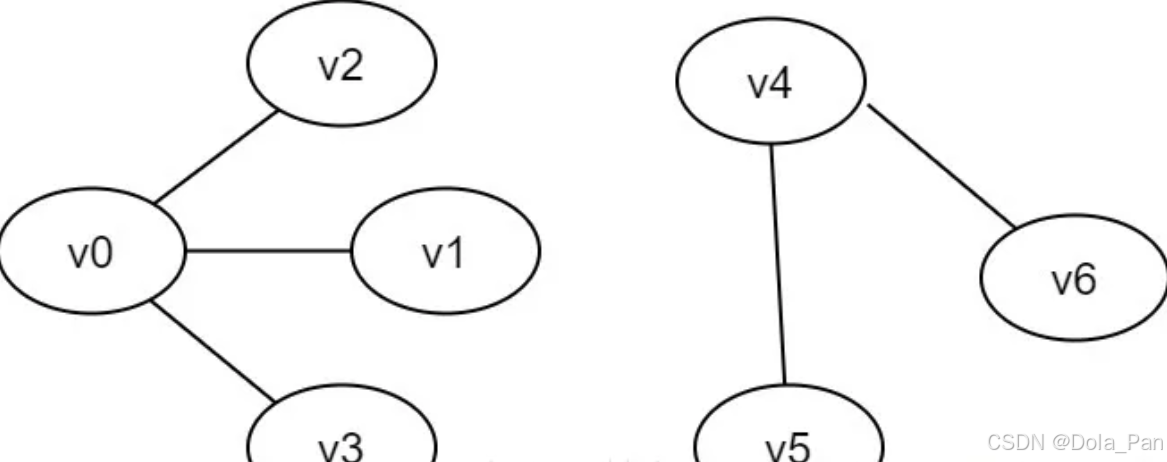
图2-3 非连通图示例

广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图2-1-1所示，要想遍历从v0到v6的每一个顶点，我们可以设v0为第一层，v1、v2、v3为第二层，v4、v5为第三层，v6为第四层，再逐个遍历每一层的每个顶点。

具体过程如下：

1. 准备工作：
   • 创建一个visited数组，用来记录已被访问过的顶点；
   • 创建一个队列，用来存放每一层的顶点；
   • 初始化图G。
2. 从图中的v0开始访问，将的visited[v0]数组的值设置为true，同时将v0入队。
3. 只要队列不空，则重复如下操作：

白色表示未被访问，灰色表示即将访问，黑色表示已访问。

visited数组：0表示未访问，1表示以访问。

队列：队头出元素，队尾进元素。

1. 初始时全部顶点均未被访问，visited数组初始化为0，队列中没有元素。

图3-2-1

1. 即将访问顶点v0。

图3-2-2

1. 访问顶点v0，并置visited[0]的值为1，同时将v0入队。

图3-2-3

1. 将v0出队，访问v0的邻接点v2。判断visited[2]，因为visited[2]的值为0，访问v2。

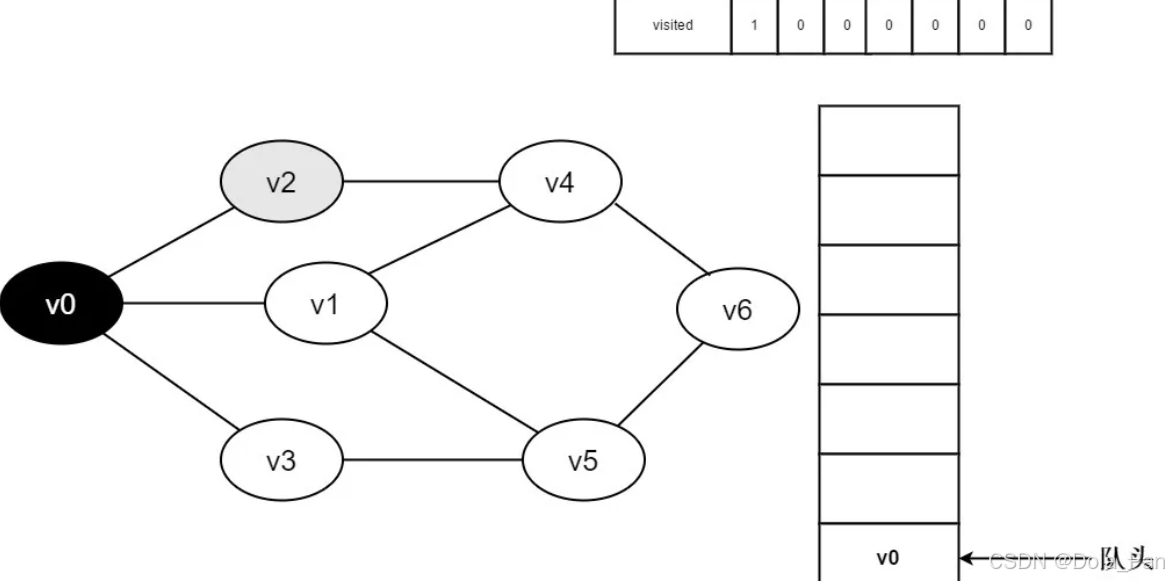
图3-2-4

1. 将visited[2]置为1，并将v2入队。

图3-2-5

1. 访问v0邻接点v1。判断visited[1],因为visited[1]的值为0，访问v1。

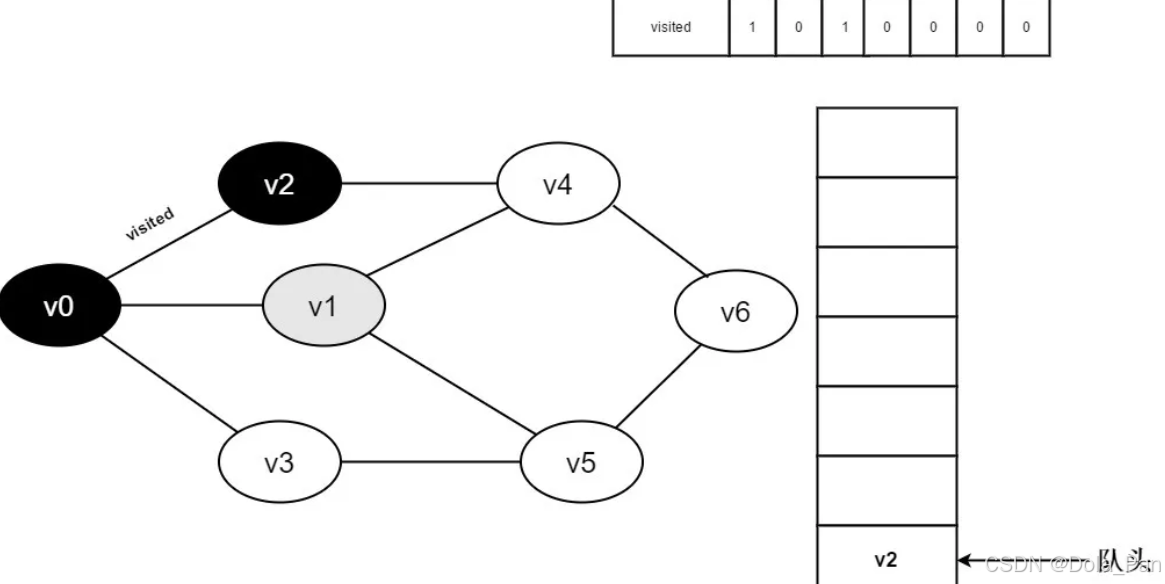
图3-2-6

1. 将visited[1]置为0，并将v1入队。

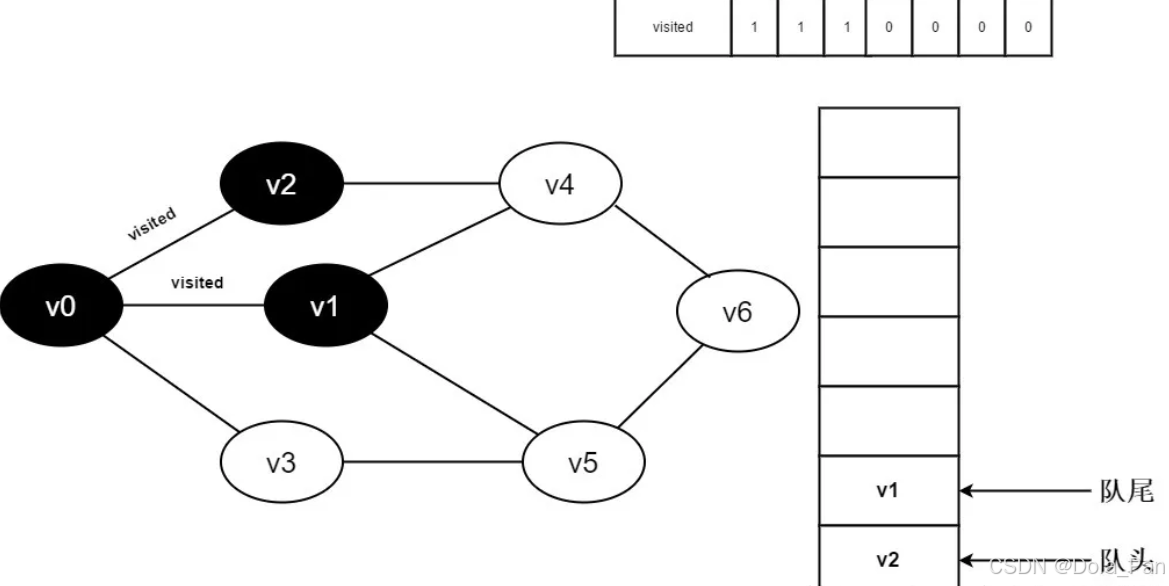
图3-2-7

1. 判断visited[3],因为它的值为0，访问v3。将visited[3]置为0，并将v3入队。

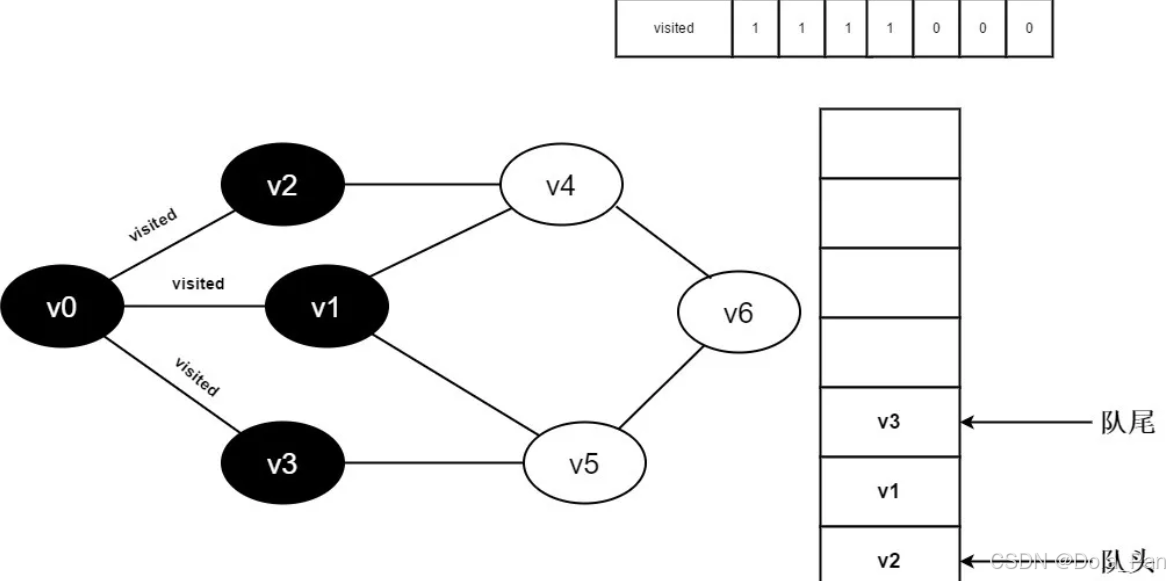
图3-2-8

1. v0的全部邻接点均已被访问完毕。将队头元素v2出队，开始访问v2的所有邻接点。

   开始访问v2邻接点v0，判断visited[0]，因为其值为1，不进行访问。

   继续访问v2邻接点v4，判断visited[4]，因为其值为0，访问v4，如下图：

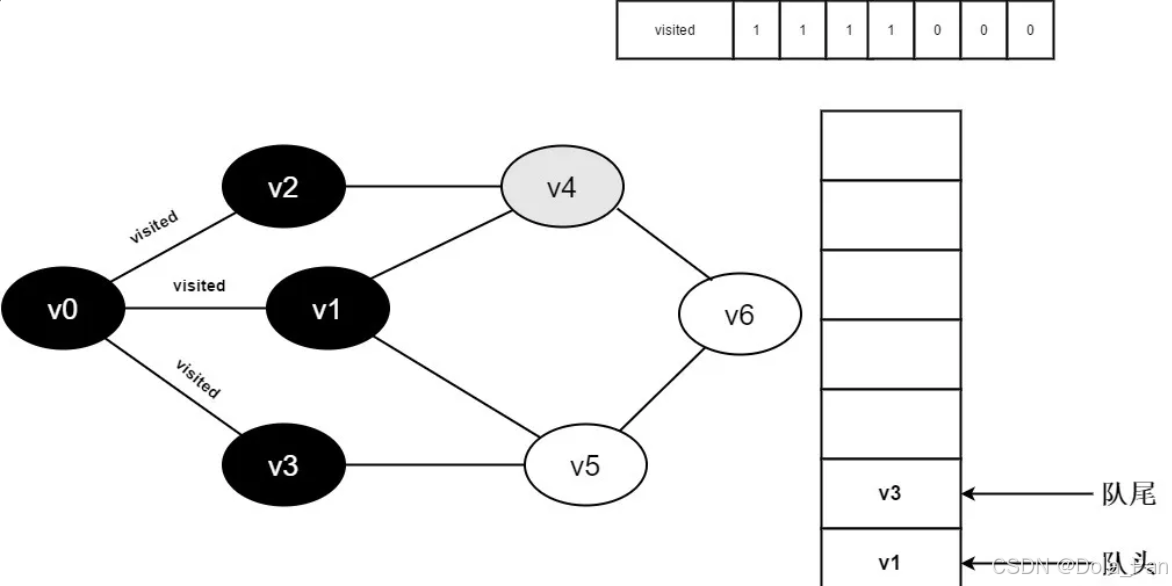
图3-2-9

1. 将visited[4]置为1，并将v4入队。

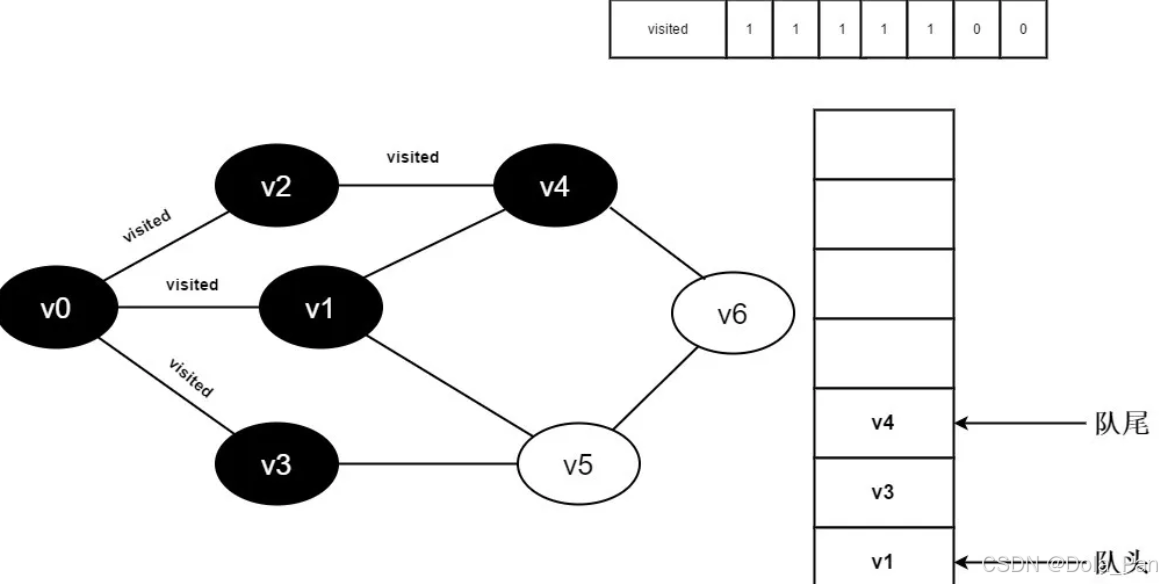
图3-2-10

1. v2的全部邻接点均已被访问完毕。将队头元素v1出队，开始访问v1的所有邻接点。

   开始访问v1邻接点v0，因为visited[0]值为1，不进行访问。

   继续访问v1邻接点v4，因为visited[4]的值为1，不进行访问。

   继续访问v1邻接点v5，因为visited[5]值为0，访问v5，如下图：

图3-2-11

1. 将visited[5]置为1，并将v5入队。

图3-2-12

1. v1的全部邻接点均已被访问完毕，将队头元素v3出队，开始访问v3的所有邻接点。

   开始访问v3邻接点v0，因为visited[0]值为1，不进行访问。

   继续访问v3邻接点v5，因为visited[5]值为1，不进行访问。

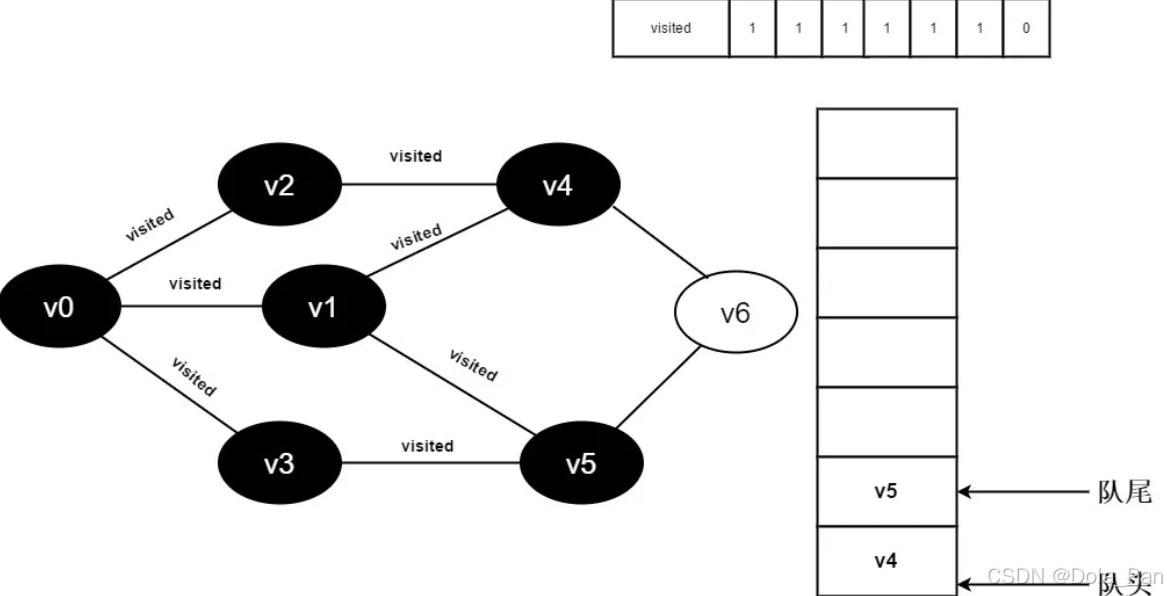
图3-2-13

1. v3的全部邻接点均已被访问完毕，将队头元素v4出队，开始访问v4的所有邻接点。

   开始访问v4的邻接点v2，因为visited[2]的值为1，不进行访问。

   继续访问v4的邻接点v6，因为visited[6]的值为0，访问v6，如下图：

图3-2-14

1. 将visited[6]值为1，并将v6入队。

图3-2-15

1. v4的全部邻接点均已被访问完毕，将队头元素v5出队，开始访问v5的所有邻接点。

   开始访问v5邻接点v3，因为visited[3]的值为1，不进行访问。

   继续访问v5邻接点v6，因为visited[6]的值为1，不进行访问。

图3-2-16

1. v5的全部邻接点均已被访问完毕，将队头元素v6出队，开始访问v6的所有邻接点。

   开始访问v6邻接点v4，因为visited[4]的值为1，不进行访问。

   继续访问v6邻接点v5，因为visited[5]的值文1，不进行访问。

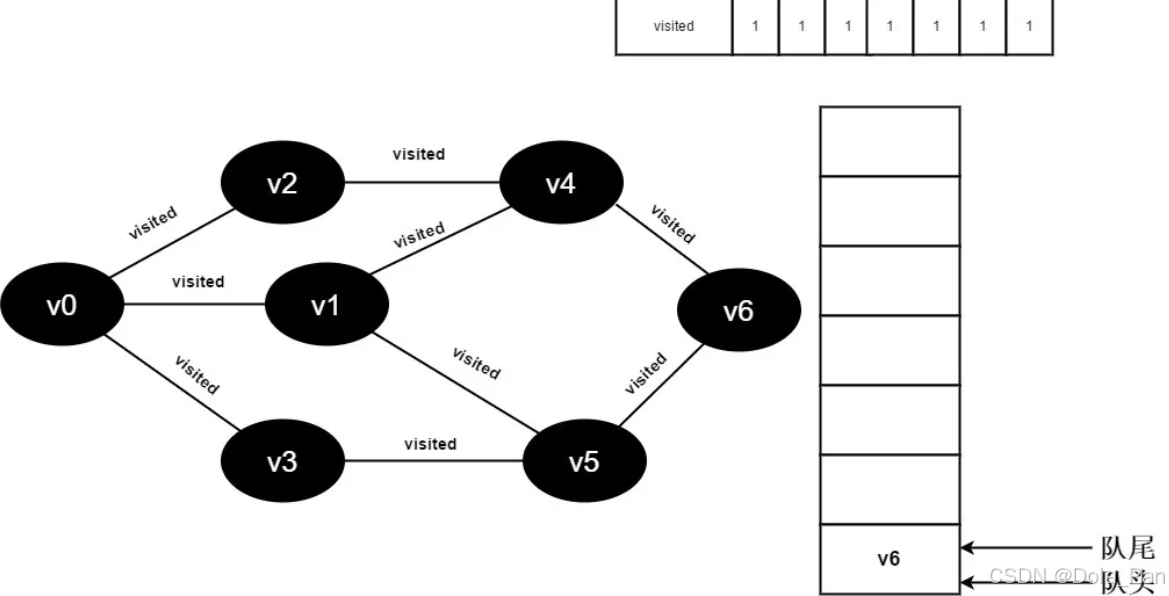
图3-2-17

1. 队列为空，退出循环，全部顶点均访问完毕。

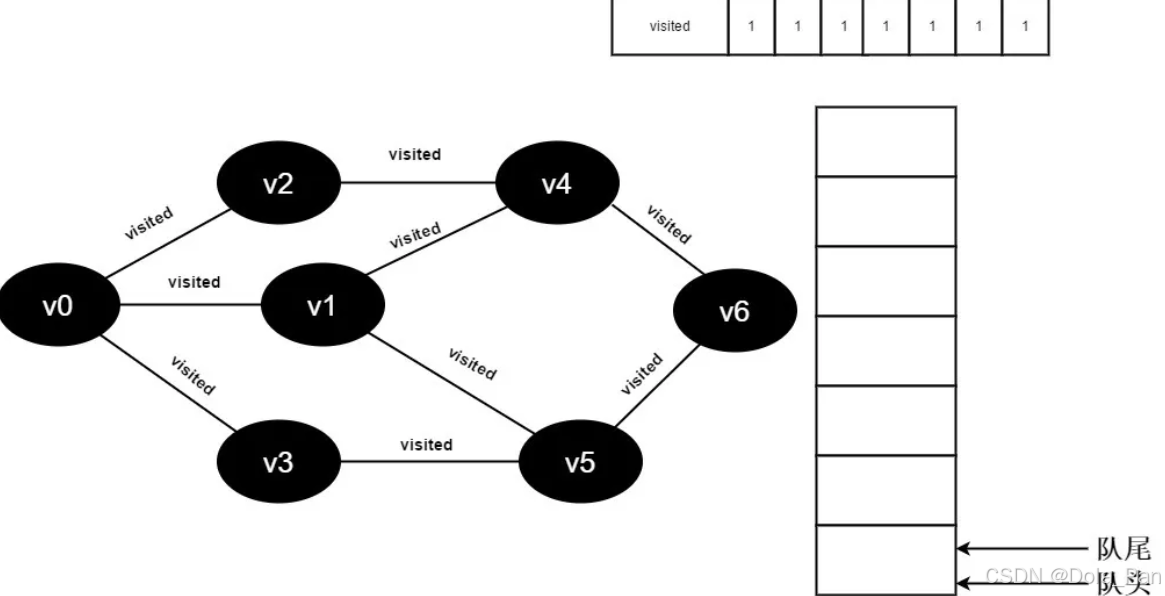
图3-2-18

3.3.1用邻接矩阵表示图的广度优先搜索

3.3.2用邻接表表示图的广度优先搜索

深度优先搜索类似于树的先序遍历，具体过程如下：

准备工作：创建一个visited数组，用于记录所有被访问过的顶点。

1. 从图中v0出发，访问v0。
2. 找出v0的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。
3. 返回前一个访问过的仍有未被访问邻接点的顶点，继续访问该顶点的下一个未被访问领接点。
4. 重复2,3步骤，直至所有顶点均被访问，搜索结束。

1. 初始时所有顶点均未被访问，visited数组为空。

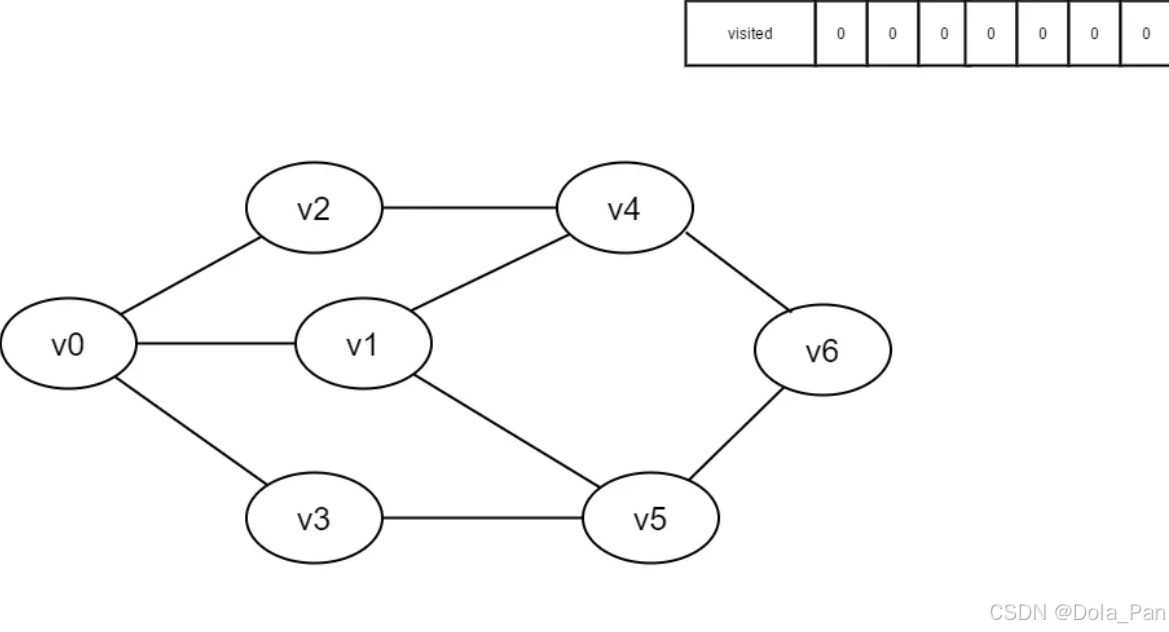
图4-2-1

1. 即将访问v0。

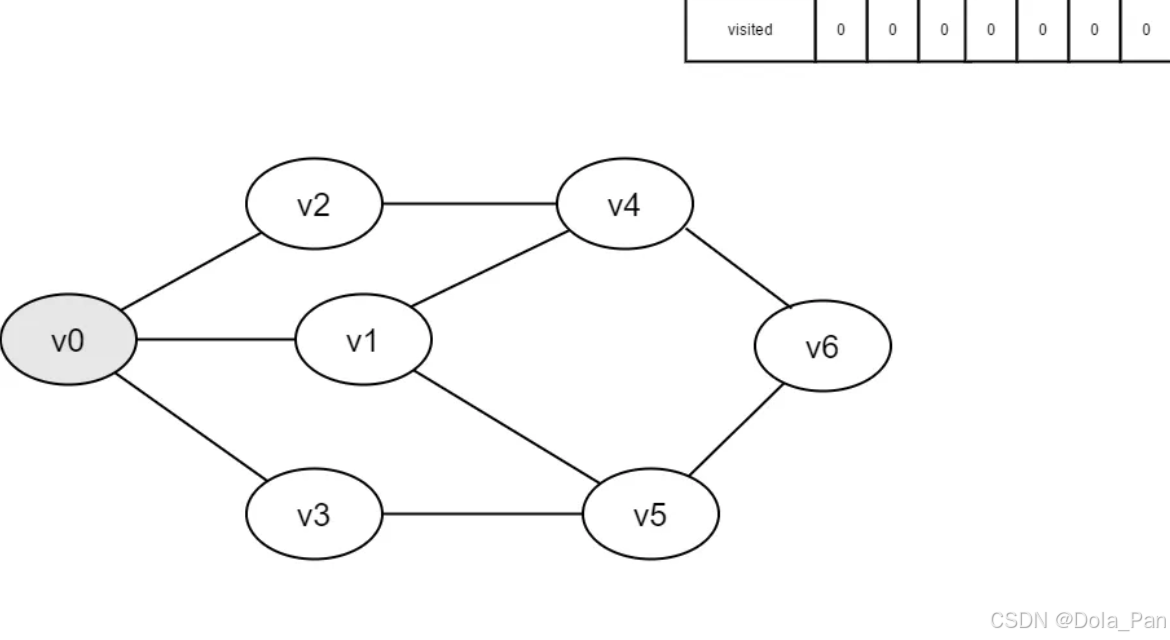
图4-2-2

1. 访问v0，并将visited[0]的值置为1。

图4-2-3

1. 访问v0的邻接点v2，判断visited[2]，因其值为0，访问v2。

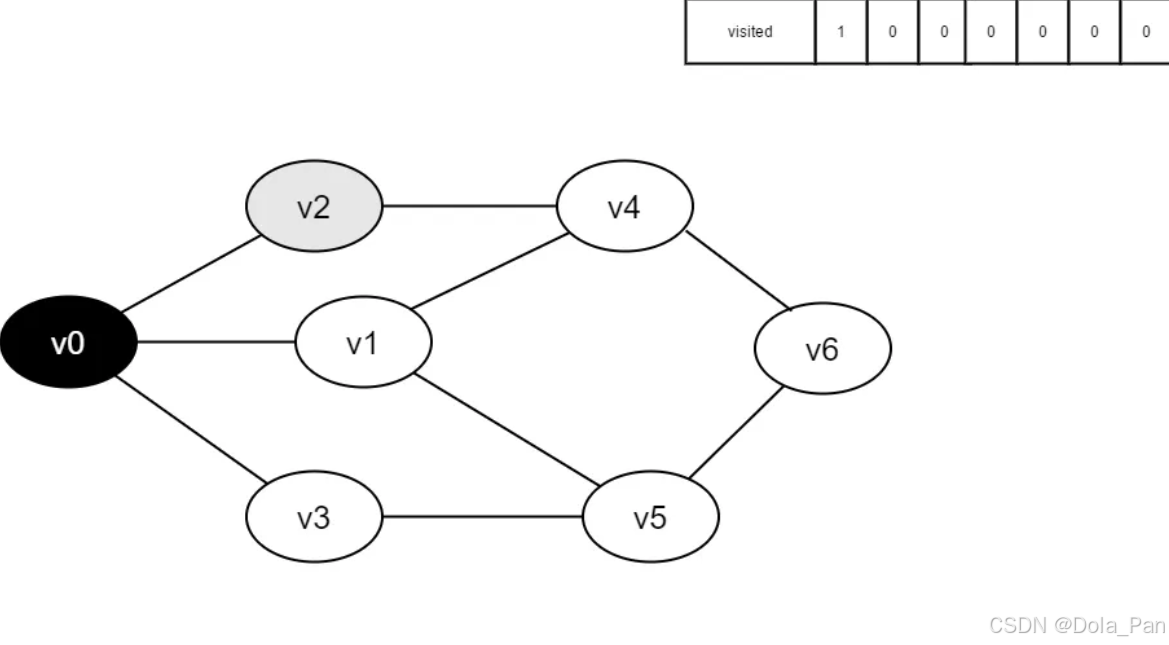
图4-2-4

1. 将visited[2]置为1。

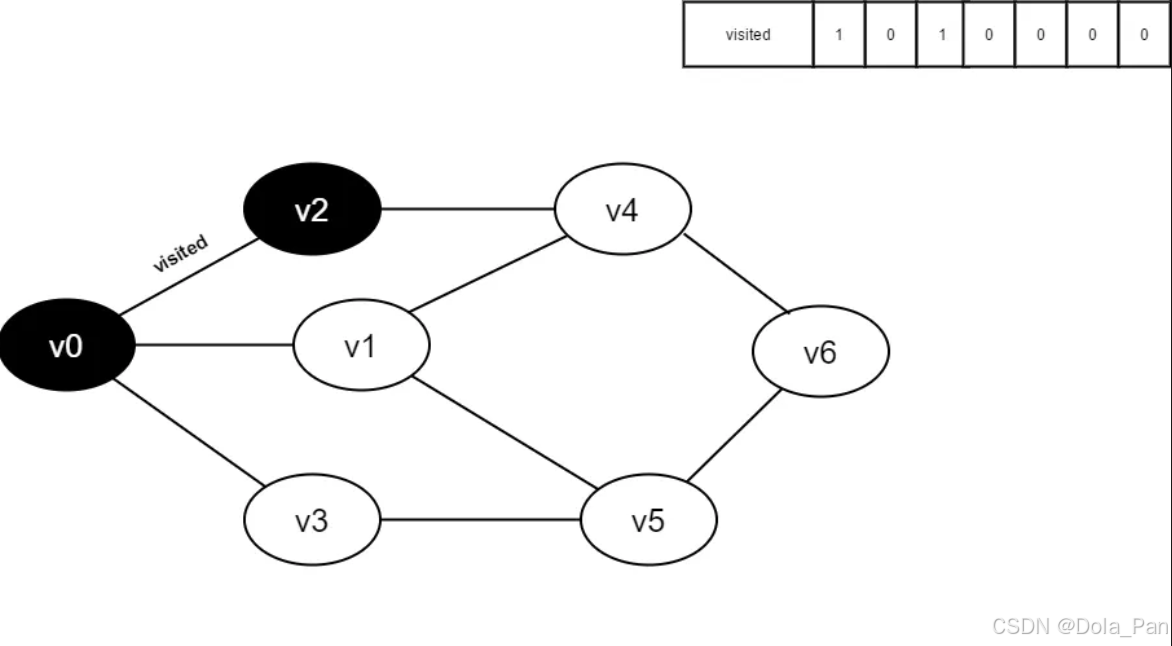
图4-2-5

1. 访问v2的邻接点v0，判断visited[0]，其值为1，不访问。

   继续访问v2的邻接点v4，判断visited[4]，其值为0，访问v4。

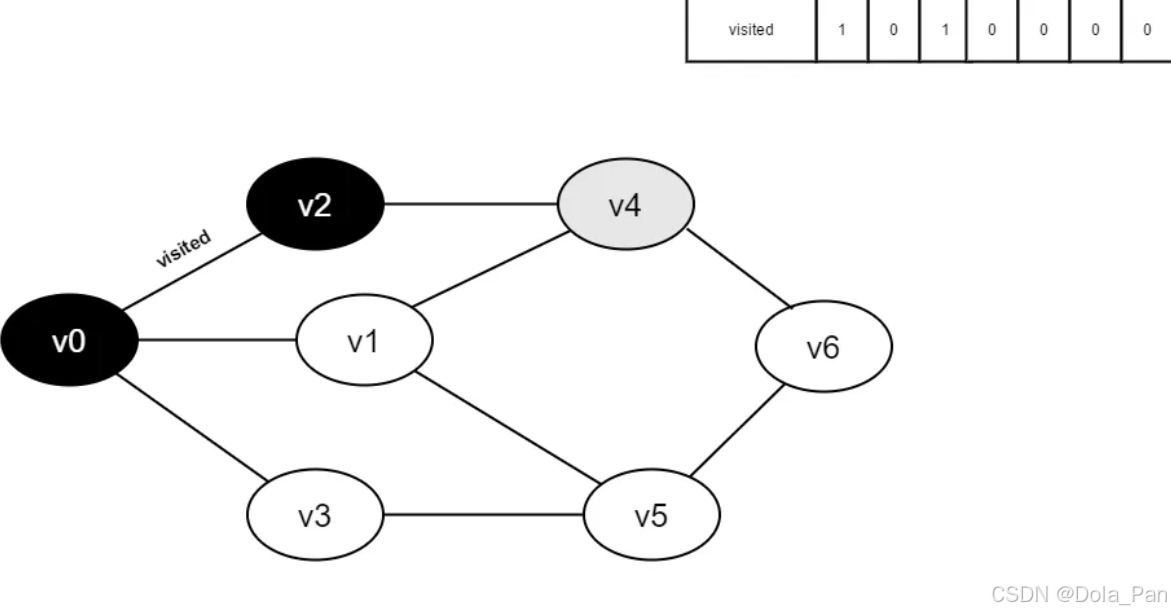
图4-2-6

1. 将visited[4]置为1。

图4-2-7

1. 访问v4的邻接点v1，判断visited[1]，其值为0，访问v1。

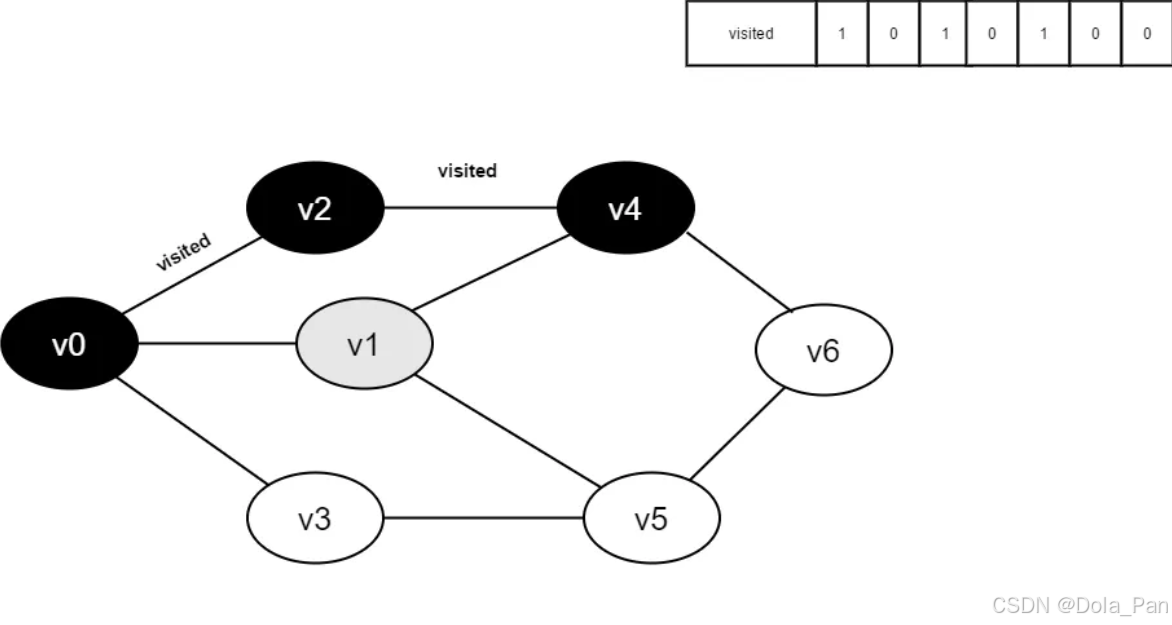
图4-2-8

1. 将visited[1]置为1。

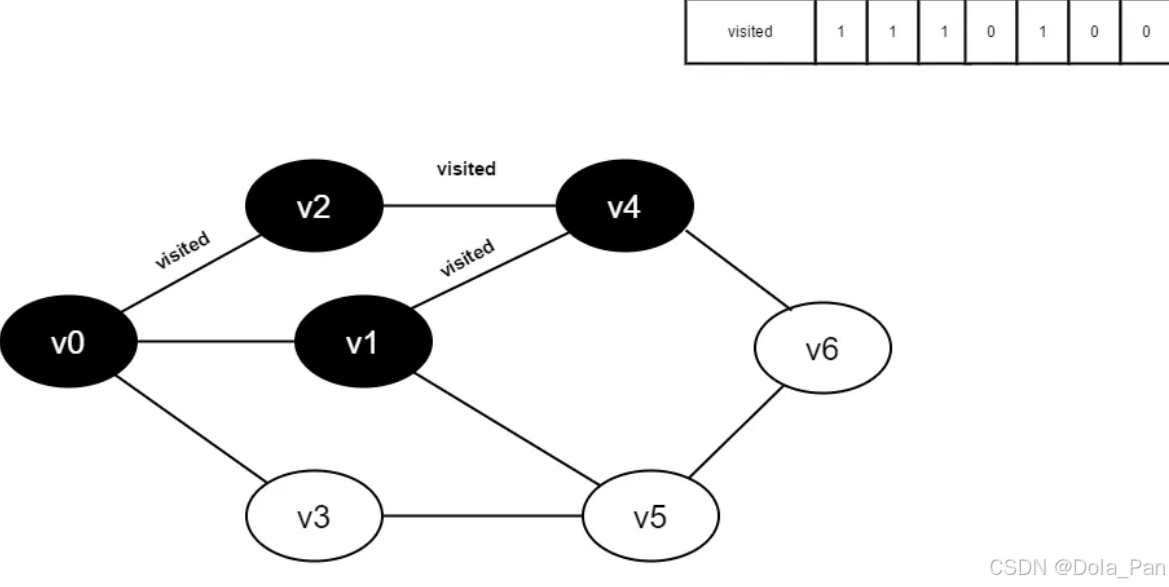
图4-2-9

1. 访问v1的邻接点v0，判断visited[0]，其值为1，不访问。

   继续访问v1的邻接点v4，判断visited[4]，其值为1，不访问。

   继续访问v1的邻接点v5，判读visited[5]，其值为0，访问v5。

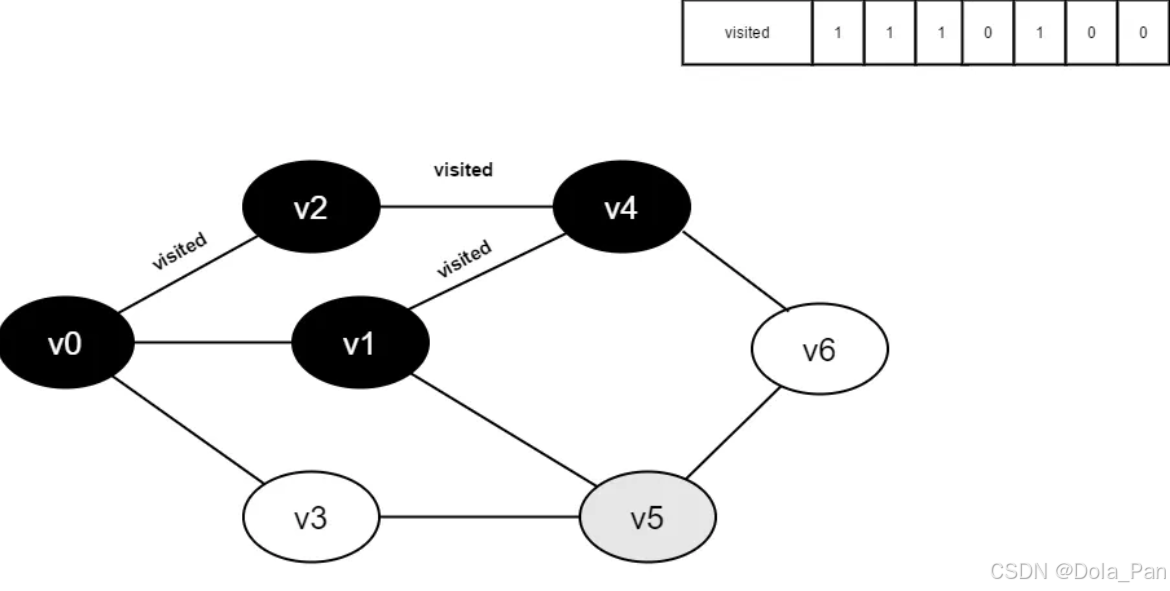
图4-2-10

1. 将visited[5]置为1。

图4-2-11

1. 访问v5的邻接点v1，判断visited[1]，其值为1，不访问。

   继续访问v5的邻接点v3，判断visited[3]，其值为0，访问v3。

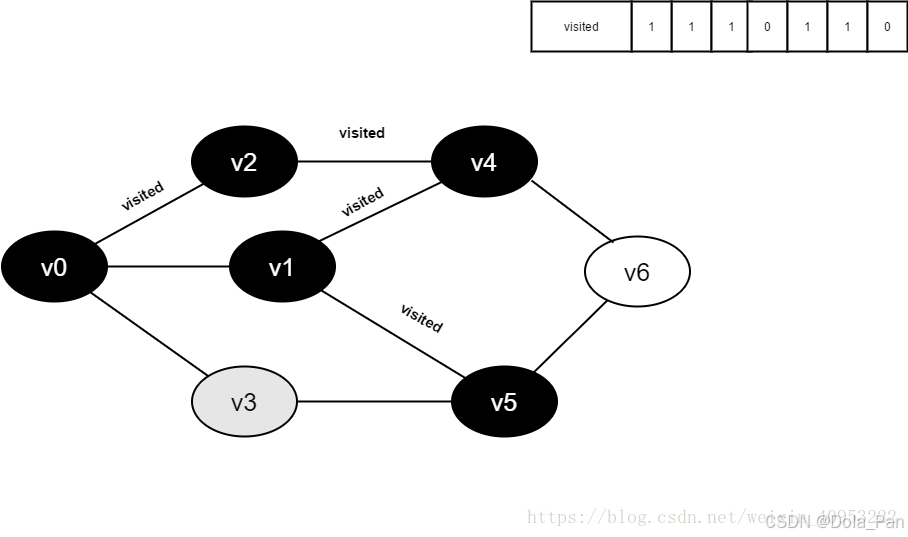
图4-2-12

1. 将visited[1]置为1。

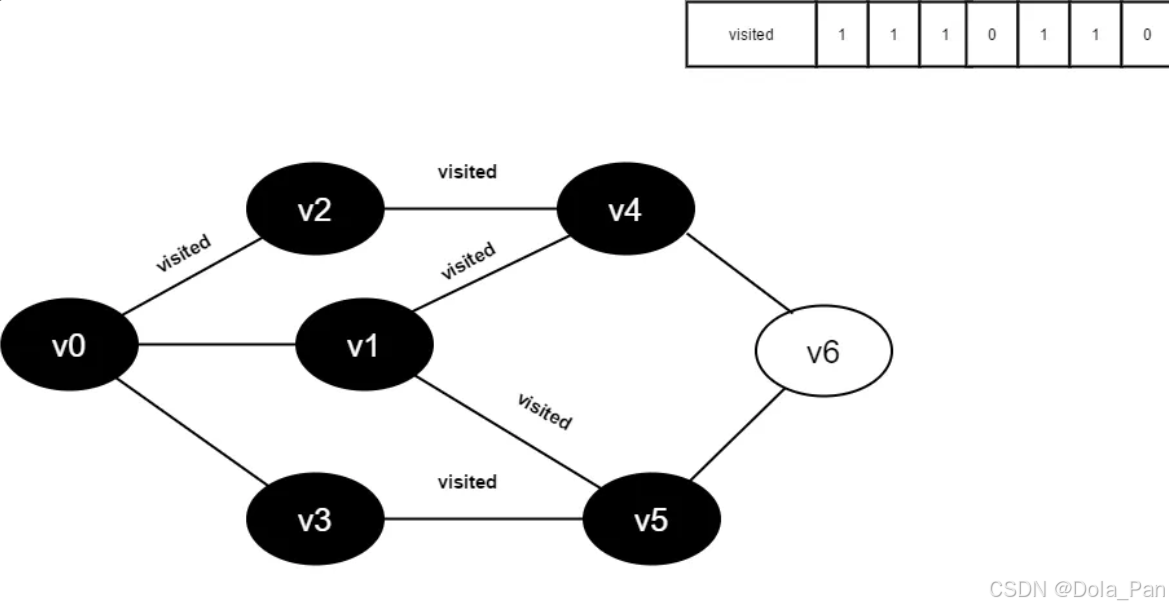
图4-2-13

1. 访问v3的邻接点v0，判断visited[0]，其值为1，不访问。

   继续访问v3的邻接点v5，判断visited[5]，其值为1，不访问。

   v3所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5所有邻接点。

   访问v5的邻接点v6，判断visited[6]，其值为0，访问v6。

图4-2-14

1. 将visited[6]置为1。

图4-2-15

1. 访问v6的邻接点v4，判断visited[4]，其值为1，不访问。

   访问v6的邻接点v5，判断visited[5]，其值为1，不访问。

   v6所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5剩余邻接点。

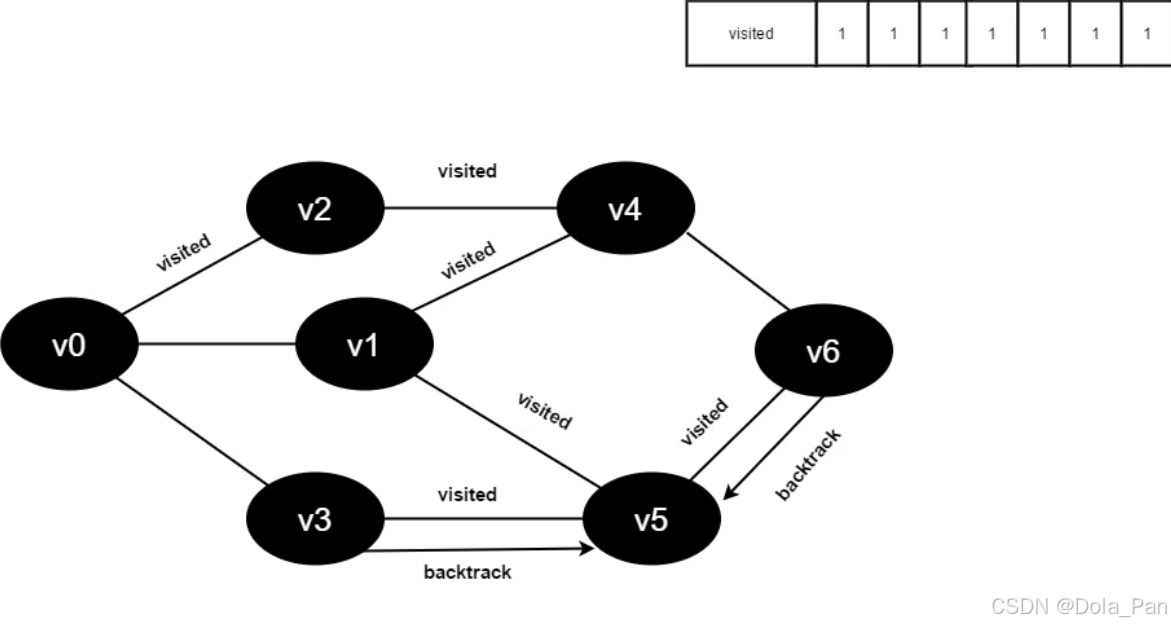
图4-2-16

1. v5所有邻接点均已被访问，回溯到其上一个顶点v1。

   v1所有邻接点均已被访问，回溯到其上一个顶点v4，遍历v4剩余邻接点v6。

   v4所有邻接点均已被访问，回溯到其上一个顶点v2。

   v2所有邻接点均已被访问，回溯到其上一个顶点v1，遍历v1剩余邻接点v3。

   v1所有邻接点均已被访问，搜索结束。

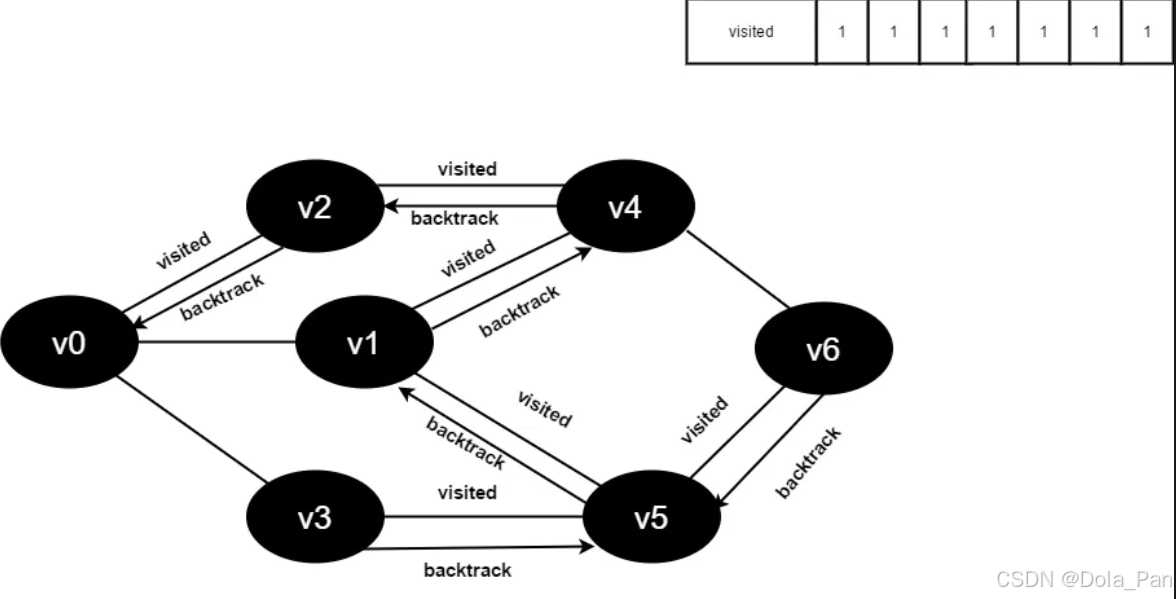
图4-2-17

4.3.1用邻接矩阵表示图的深度优先搜索

邻接矩阵的创建在上述已描述过，这里不再赘述

4.3.2用邻接表表示图的深度优先搜素

邻接表的创建在上述已描述过，这里不再赘述。

到此这篇bfs广度优先搜索（广度优先搜索使用的辅助空间是什么）的文章就介绍到这了,更多相关内容请继续浏览下面的相关 推荐文章，希望大家都能在编程的领域有一番成就！

版权声明：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/bcyy/14756.html