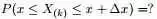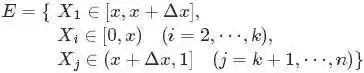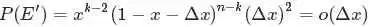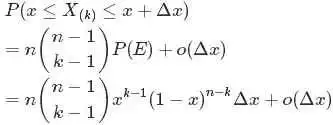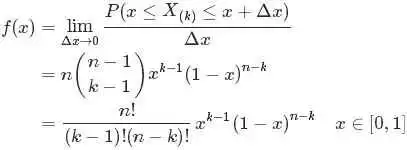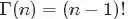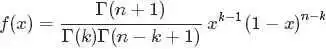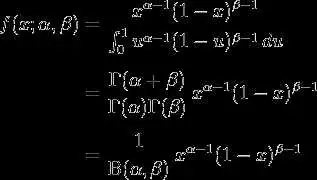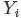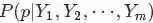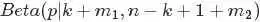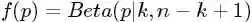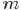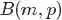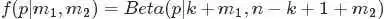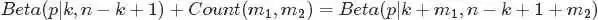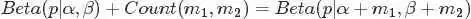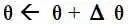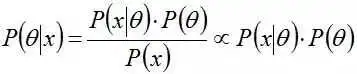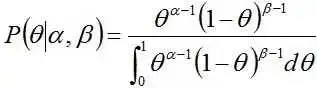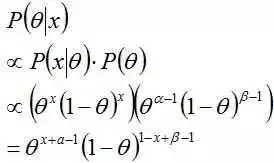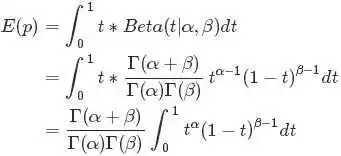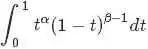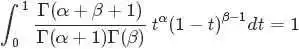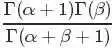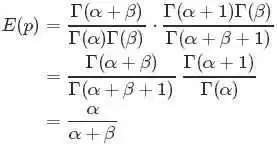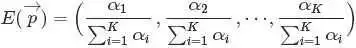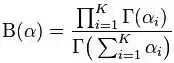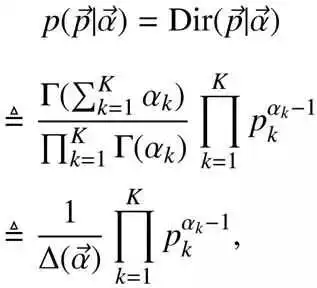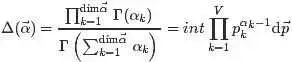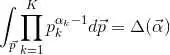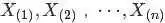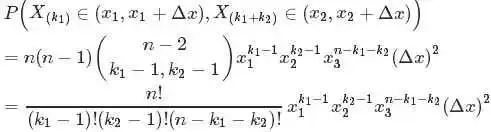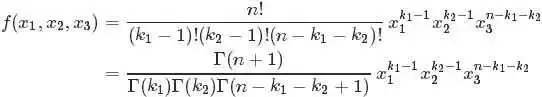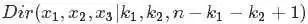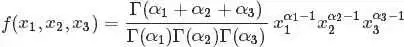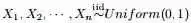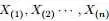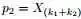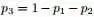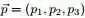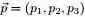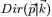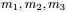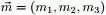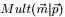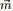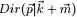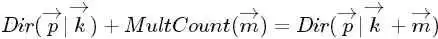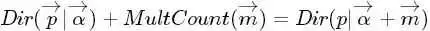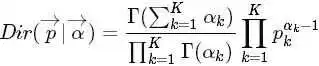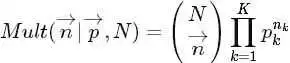作者:v_JULY_v
来源:http://blog.csdn.net/v_july_v/article/details/
本文按照以下5个步骤来阐述,希望读者看完本文后,能对LDA有个尽量清晰完整的了解。
关于LDA有两种含义,一种是线性判别分析(Linear Discriminant Analysis),一种是概率主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),本文讲后者。
另外,我先简单说下LDA的整体思想,不然我怕你看了半天,铺了太长的前奏,却依然因没见到LDA的影子而显得“心浮气躁”,导致不想再继续看下去。所以,先给你吃一颗定心丸,明白整体框架后,咱们再一步步抽丝剥茧,展开来论述。
按照wiki上的介绍,LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,是一种主题模型,它可以将文档集 中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。此外,一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
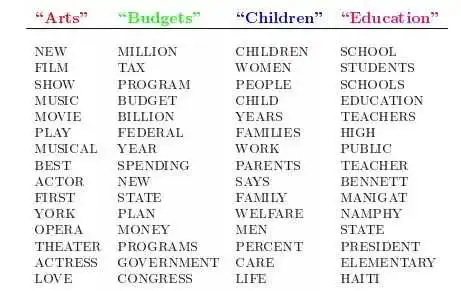
人类是怎么生成文档的呢?LDA的这三位作者在原始论文中给了一个简单的例子。比如假设事先给定了这几个主题:Arts、Budgets、Children、Education,然后通过学习的方式,获取每个主题Topic对应的词语。如下图所示:
然后以一定的概率选取上述某个主题,再以一定的概率选取那个主题下的某个单词,不断的重复这两步,最终生成如下图所示的一篇文章(其中不同颜色的词语分别对应上图中不同主题下的词):
而当我们看到一篇文章后,往往喜欢推测这篇文章是如何生成的,我们可能会认为作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文。LDA就是要干这事:根据给定的一篇文档,推测其主题分布。
通俗来说,人类根据上述文档生成过程写成了各种各样的文章,现在某小撮人想让计算机利用LDA干一件事:你计算机给我分析推测网络上各篇文章分别都写了些啥主题,且各篇文章中各个主题出现的概率大小(主题分布)是啥。
然,就是这么一个看似普通的LDA,一度吓退了不少想深入探究其内部原理的初学者。难在哪呢,难就难在LDA内部涉及到的数学知识点太多了。
在LDA模型中,一篇文档生成的方式如下:
- 从狄利克雷分布
 中取样生成文档 i 的主题分布
中取样生成文档 i 的主题分布
- 从主题的多项式分布
 中取样生成文档i第 j 个词的主题
中取样生成文档i第 j 个词的主题
- 从狄利克雷分布
 中取样生成主题
中取样生成主题 对应的词语分布
对应的词语分布
- 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语
其中,类似Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布。
此外,LDA的图模型结构如下图所示(类似贝叶斯网络结构):
恩,不错,短短6句话整体概括了整个LDA的主体思想!但也就是上面短短6句话,却接连不断或重复出现了二项分布、多项式分布、beta分布、狄利克雷分布(Dirichlet分布)、共轭先验概率分布、取样,那么请问,这些都是啥呢?
今天我们先简单解释下二项分布、多项分布、beta分布、Dirichlet 分布这4个分布。后续会介绍更多LDA的详细内容。
- 二项分布(Binomial distribution)
二项分布是从伯努利分布推进的。伯努利分布,又称两点分布或0-1分布,是一个离散型的随机分布,其中的随机变量只有两类取值,非正即负{+,-}。而二项分布即重复n次的伯努利试验,记为  。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。二项分布的概率密度函数为:
。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。二项分布的概率密度函数为:
对于k = 0, 1, 2, ..., n,其中的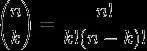 是二项式系数(这就是二项分布的名称的由来),又记为
是二项式系数(这就是二项分布的名称的由来),又记为 。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数
。回想起高中所学的那丁点概率知识了么:想必你当年一定死记过这个二项式系数 就是
就是 。
。
- 多项分布,是二项分布扩展到多维的情况。
多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3...,k)。比如投掷6个面的骰子实验,N次实验结果服从K=6的多项分布。其中
多项分布的概率密度函数为:
- Beta分布,二项分布的共轭先验分布。
给定参数 和
和 ,取值范围为[0,1]的随机变量 x 的概率密度函数:
,取值范围为[0,1]的随机变量 x 的概率密度函数:
其中:
,
。
注: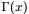 便是所谓的gamma函数,下文会具体阐述。
便是所谓的gamma函数,下文会具体阐述。
- Dirichlet分布,是beta分布在高维度上的推广。
Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙:
其中
至此,我们可以看到二项分布和多项分布很相似,Beta分布和Dirichlet 分布很相似,而至于“Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布”这点在下文中说明。
OK,接下来,咱们就按照本文开头所说的思路:“一个函数:gamma函数,四个分布:二项分布、多项分布、beta分布、Dirichlet分布,外加一个概念和一个理念:共轭先验和贝叶斯框架,两个模型:pLSA、LDA(文档-主题,主题-词语),一个采样:Gibbs采样”一步步详细阐述,争取给读者一个尽量清晰完整的LDA。
(当然,如果你不想深究背后的细节原理,只想整体把握LDA的主体思想,可直接跳到本文,等着后面我们再推送的文章,若后面还是想深究背后的细节原理,可再回到本文开始看)
咱们先来考虑一个问题(此问题1包括下文的问题2-问题4皆取材自LDA数学八卦):
- 问题1 随机变量

- 把这n 个随机变量排序后得到顺序统计量

- 然后请问
 的分布是什么。
的分布是什么。
为解决这个问题,可以尝试计算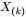 落在区间[x,x+Δx]的概率。即求下述式子的值:
落在区间[x,x+Δx]的概率。即求下述式子的值:
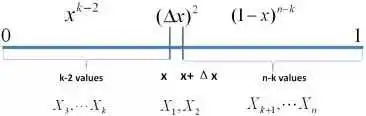
首先,把 [0,1] 区间分成三段 [0,x),[x,x+Δx],(x+Δx,1],然后考虑下简单的情形:即假设n 个数中只有1个落在了区间 [x,x+Δx]内,由于这个区间内的数X(k)是第k大的,所以[0,x)中应该有 k−1 个数,(x+Δx,1] 这个区间中应该有n−k 个数。如下图所示:
从而问题转换为下述事件E:
对于上述事件E,有:
其中,o(Δx)表示Δx的高阶无穷小。显然,由于不同的排列组合,即n个数中有一个落在 [x,x+Δx]区间的有n种取法,余下n−1个数中有k−1个落在[0,x)的有 种组合,所以和事件E等价的事件一共有
种组合,所以和事件E等价的事件一共有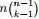 个。
个。
如果有2个数落在区间[x,x+Δx]呢?如下图所示:
类似于事件E,对于2个数落在区间[x,x+Δx]的事件E’:
有:
从上述的事件E、事件E‘中,可以看出,只要落在[x,x+Δx]内的数字超过一个,则对应的事件的概率就是 o(Δx)。于是乎有:
从而得到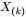 的概率密度函数
的概率密度函数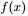 为:
为:
至此,本节开头提出的问题得到解决。然仔细观察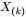 的概率密度函数,发现式子的最终结果有阶乘,联想到阶乘在实数上的推广
的概率密度函数,发现式子的最终结果有阶乘,联想到阶乘在实数上的推广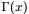 函数:
函数:
两者结合是否会产生奇妙的效果呢?考虑到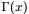 具有如下性质:
具有如下性质:
故将代入到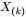 的概率密度函数
的概率密度函数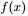 中,可得:
中,可得:
然后取 ,
, ,转换
,转换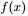 得到:
得到:
如果熟悉beta分布的朋友,可能会惊呼:哇,竟然推出了beta分布!
在概率论中,beta是指一组定义在 区间的连续概率分布,有两个参数
区间的连续概率分布,有两个参数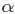 和
和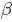
,且 。
。
beta分布的概率密度函数是:
其中的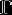 便是
便是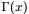 函数:
函数:
随机变量X服从参数为的beta分布通常写作: 。
。
回顾下1.1节开头所提出的问题:“问题1 随机变量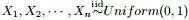 ,把这n 个随机变量排序后得到顺序统计量
,把这n 个随机变量排序后得到顺序统计量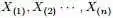 ,然后请问
,然后请问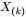 的分布是什么。” 如果,咱们要在这个问题的基础上增加一些观测数据,变成问题2:
的分布是什么。” 如果,咱们要在这个问题的基础上增加一些观测数据,变成问题2:
 ,对应的顺序统计量是
,对应的顺序统计量是 ,需要猜测
,需要猜测 ;
; ,
,  中有
中有 个比p小,
个比p小, 个比
个比 大;
大;- 那么,请问
 的分布是什么。
的分布是什么。
根据“Yi中有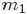 个比
个比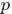 小,
小,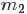 个比
个比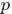 大”,换言之,Yi中有
大”,换言之,Yi中有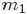 个比
个比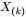 小,
小,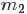 个比
个比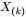 大,所以
大,所以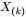 是
是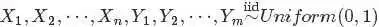 中第
中第 大的数。
大的数。
根据1.1节最终得到的结论“只要落在[x,x+Δx]内的数字超过一个,则对应的事件的概率就是 o(Δx)”,继而推出事件服从beta分布,从而可知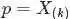 的概率密度函数为:
的概率密度函数为:
熟悉贝叶斯方法(不熟悉的没事,参见此文第一部分)的朋友心里估计又犯“嘀咕”了,这不就是贝叶斯式的思考过程么?
- 为了猜测
 ,在获得一定的观测数据前,我们对
,在获得一定的观测数据前,我们对 的认知是:
的认知是: ,此称为
,此称为 的先验分布;
的先验分布; - 然后为了获得这个结果“
 中有
中有 个比p小,
个比p小, 个比
个比 大”,针对
大”,针对 是做了
是做了 次贝努利实验,所以
次贝努利实验,所以 服从二项分布
服从二项分布 ;
; - 在给定了来自数据提供的
 的知识后,
的知识后, 的后验分布变为
的后验分布变为 。
。
回顾下贝叶斯派思考问题的固定模式:
- 先验分布
 + 样本信息
+ 样本信息
 后验分布
后验分布
上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对 的认知是先验分布
的认知是先验分布 ,在得到新的样本信息
,在得到新的样本信息 后,人们对
后,人们对 的认知为
的认知为 。
。
类比到现在这个问题上,我们也可以试着写下:
其中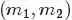 对应的是二项分布
对应的是二项分布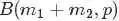 的计数。
的计数。
更一般的,对于非负实数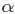 和
和 ,我们有如下关系
,我们有如下关系
针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial共轭。换言之,Beta分布是二项式分布的共轭先验概率分布。
二项分布和Beta分布是共轭分布意味着,如果我们为二项分布的参数p选取的先验分布是Beta分布,那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布。
此外,如何理解参数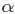 和
和 所表达的意义呢?
所表达的意义呢?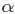 、
、 可以认为形状参数,通俗但不严格的理解是,
可以认为形状参数,通俗但不严格的理解是,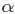 和
和 共同控制Beta分布的函数“长的样子”:形状千奇百怪,高低胖瘦,如下图所示:
共同控制Beta分布的函数“长的样子”:形状千奇百怪,高低胖瘦,如下图所示:
什么又是共轭呢?轭的意思是束缚、控制,共轭从字面上理解,则是共同约束,或互相约束。
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么,先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
比如,某观测数据服从概率分布P(θ)时,当观测到新的X数据时,我们一般会遇到如下问题:
- 可否根据新观测数据X,更新参数θ?
- 根据新观测数据可以在多大程度上改变参数θ,即
- 当重新估计θ的时候,给出新参数值θ的新概率分布,即P(θ|x)。
事实上,根据根据贝叶斯公式可知:
其中,P(x|θ)表示以预估θ为参数的x概率分布,可以直接求得,P(θ)是已有原始的θ概率分布。
所以,如果我们选取P(x|θ)的共轭先验作为P(θ)的分布,那么P(x|θ)乘以P(θ),然后归一化的结果P(θ|x)跟和P(θ)的形式一样。换句话说,先验分布是P(θ),后验分布是P(θ|x),先验分布跟后验分布同属于一个分布族,故称该分布族是θ的共轭先验分布(族)。
举个例子。投掷一个非均匀硬币,可以使用参数为θ的伯努利模型,θ为硬币为正面的概率,那么结果x的分布形式为:
其共轭先验为beta分布,具有两个参数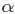 和
和 ,称为超参数(hyperparameters)。且这两个参数决定了θ参数,其Beta分布形式为
,称为超参数(hyperparameters)。且这两个参数决定了θ参数,其Beta分布形式为
然后计算后验概率
归一化这个等式后会得到另一个Beta分布,从而证明了Beta分布确实是伯努利分布的共轭先验分布。
接下来,咱们来考察beta分布的一个性质。
如果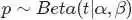 ,则有:
,则有:
注意到上式最后结果的右边积分
其类似于概率分布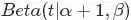 ,而对于这个分布有
,而对于这个分布有
从而求得
的结果为
最后将此结果带入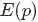 的计算式,得到:
的计算式,得到:
最后的这个结果意味着对于Beta 分布的随机变量,其均值(期望)可以用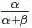 来估计。此外,狄利克雷Dirichlet 分布也有类似的结论,即如果
来估计。此外,狄利克雷Dirichlet 分布也有类似的结论,即如果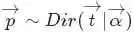 ,同样可以证明有下述结论成立:
,同样可以证明有下述结论成立:
那什么是Dirichlet 分布呢?简单的理解Dirichlet 分布就是一组连续多变量概率分布,是多变量普遍化的beta分布。为了纪念德国数学家约翰·彼得·古斯塔夫·勒热纳·狄利克雷(Peter Gustav Lejeune Dirichlet)而命名。狄利克雷分布常作为贝叶斯统计的先验概率。
根据wikipedia上的介绍,维度K ≥ 2(x1,x2…xK-1维,共K个)的狄利克雷分布在参数α1, ..., αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数,定义为:
其中,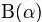 相当于是多项beta函数
相当于是多项beta函数
且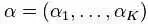
此外,x1+x2+…+xK-1+xK=1,x1,x2…xK-1>0,且在(K-1)维的单纯形上,其他区域的概率密度为0。
当然,也可以如下定义Dirichlet 分布
其中的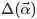 称为Dirichlet 分布的归一化系数:
称为Dirichlet 分布的归一化系数:
且根据Dirichlet分布的积分为1(概率的基本性质),可以得到:
下面,在2.2节问题2的基础上继续深入,引出问题3。
 ,
,- 排序后对应的顺序统计量
 ,
, - 问
 的联合分布是什么?
的联合分布是什么?
为了简化计算,取x3满足x1+x2+x3=1,但只有x1,x2是变量,如下图所示:
从而有:
继而得到于是我们得到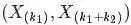 的联合分布为:
的联合分布为:
观察上述式子的最终结果,可以看出上面这个分布其实就是3维形式的 Dirichlet 分布
令 ,于是分布密度可以写为
,于是分布密度可以写为
这个就是一般形式的3维 Dirichlet 分布,即便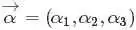 延拓到非负实数集合,以上概率分布也是良定义的。
延拓到非负实数集合,以上概率分布也是良定义的。
将Dirichlet分布的概率密度函数取对数,绘制对称Dirichlet分布的图像如下图所示(截取自wikipedia上):
上图中,取K=3,也就是有两个独立参数x1,x2,分别对应图中的两个坐标轴,第三个参数始终满足x3=1-x1-x2且α1=α2=α3=α,图中反映的是参数α从α=(0.3, 0.3, 0.3)变化到(2.0, 2.0, 2.0)时的概率对数值的变化情况。
为了论证Dirichlet分布是多项式分布的共轭先验概率分布,下面咱们继续在上述问题3的基础上再进一步,提出问题4。
- 问题4
 ,排序后对应的顺序统计量
,排序后对应的顺序统计量
- 令
 ,
, ,
, (此处的p3非变量,只是为了表达方便),现在要猜测
(此处的p3非变量,只是为了表达方便),现在要猜测 ;
;  ,Yi中落到
,Yi中落到 ,
, ,
, 三个区间的个数分别为 m1,m2,m3,m=m1+m2+m3;
三个区间的个数分别为 m1,m2,m3,m=m1+m2+m3;- 问后验分布
 的分布是什么。
的分布是什么。
为了方便讨论,记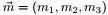 ,及
,及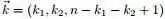 ,根据已知条件“
,根据已知条件“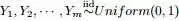 ,Yi中落到
,Yi中落到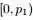 ,
,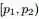 ,
,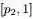 三个区间的个数分别为 m1,m2”,可得
三个区间的个数分别为 m1,m2”,可得 、
、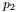 分别是这m+n个数中第
分别是这m+n个数中第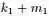 大、第
大、第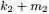 大的数。于是,后验分布
大的数。于是,后验分布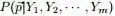 应该为
应该为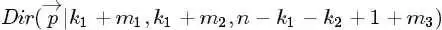 ,即一般化的形式表示为:
,即一般化的形式表示为: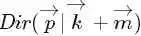 。
。
同样的,按照贝叶斯推理的逻辑,可将上述过程整理如下:
- 我们要猜测参数
 ,其先验分布为
,其先验分布为 ;
; - 数据Yi落到三个区间
 ,
, ,
, 的个数分别为
的个数分别为 ,所以
,所以 服从多项分布
服从多项分布
- 在给定了来自数据提供的知识
 后,
后, 的后验分布变为
的后验分布变为
上述贝叶斯分析过程的直观表述为:
令 ,可把
,可把 从整数集合延拓到实数集合,从而得到更一般的表达式如下:
从整数集合延拓到实数集合,从而得到更一般的表达式如下:
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是Dirichlet-Multinomial 共轭。换言之,至此已经证明了Dirichlet分布的确就是多项式分布的共轭先验概率分布。
意味着,如果我们为多项分布的参数p选取的先验分布是Dirichlet分布,那么以p为参数的多项分布用贝叶斯估计得到的后验分布仍然服从Dirichlet分布。
进一步,一般形式的Dirichlet 分布定义如下:
而对于给定的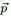 和N,其多项分布为:
和N,其多项分布为:
结论是:Dirichlet分布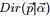 和多项分布
和多项分布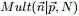 是共轭关系。
是共轭关系。
今天我们就先了解这些基础知识,请大家继续关注小君后面推出的LDA详细内容。
备注:
1、如果有题目咨询,请把题目表述清楚(备注姓名),发到公号后台。抱歉不能一 一解答。但我们会定期整理,发送推文,以供更多朋友参与交流。
2、如果您想支持本号的运营,请点击一下二维码赞赏,请不要直接在公号里发红包。否则我们只能看到如下:
谢谢理解与支持!

交流分享、谢谢支持!

版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/12038.html